3046
A fuzzy Markov random field approach for the unsupervised segmentation of hyperpolarized 13C MRI data1Department of Radiology, University of Cambridge, Cambridge, United Kingdom, 2Integrated Mathematical Oncology, Moffitt Cancer Centre, Tampa, FL, United States, 3Cancer Research UK Cambridge Institute, University of Cambridge, Cambridge, United Kingdom
Synopsis
MRI with hyperpolarized 13C-labelled compounds is an emerging clinical technique allowing in vivo metabolic processes to be characterized non-invasively. Accurate quantification of metabolism requires a region-of-interest to be defined, which is usually based on spatial information only. However, as the hyperpolarized data is 5-dimensional (spatial, temporal and spectral), it offers the possibility of applying novel segmentation methods to more accurately define this region-of-interest. A novel solution to the problem of 13C image segmentation is proposed here, using a hybrid Markov random field model with fuzzy logic. Performance of the algorithm is demonstrated using in silico and in vivo data.
Introduction
Hyperpolarized MRI with 13C-labelled compounds is an emerging clinical technique allowing \textit{in vivo} metabolic processes to be characterized non-invasively. The conversion of 13C-pyruvate to 13C-lactate has been shown to correlate with both tumor grade1 and treatment response2, however accurate and robust quantification of metabolic changes is imperative in order to make reliable inter- and intra-patient comparisons and to inform clinical decisions.
Such analysis of imaging data typically makes use of a defined region or volume of interest (VOI), however results may be very sensitive to the exact definition of the VOI. Simple methods such as thresholding are particularly unsuitable due to the interdependence of metabolite intensities and rapid dynamics. Unsupervised segmentation of 13C data offers a unique challenge due to its low spatial resolution, high noise and susceptibility to artifacts and its inherent 5-dimentionality (3D spatial, 1D temporal, 1D spectral). Here, we propose a hybrid Markov random field (MRF) model with fuzzy logic for the segmentation of 13C images, which fully incorporates spatial, temporal and spectral information whilst effectively handling the low image quality currently associated with hyperpolarized MRI.
Methods
The MRF model for image segmentation builds on an approach first suggested by Chatzis et al4, which incorporates the Gibb’s priors and multivariate Gaussian conditional function typical of MRF, into a fuzzy C-means objective function for minimization. The objective is to uncover the hidden segmentation field x given the observed noisy data y. Under a mean-field approximation to reduce computational intensity, the prior probability for a given image pixel j to belong to class i is given by:
$$p(x_{i,j}|x_{Nj},\beta) = \frac{e^{\beta(S_{i,j}+T_{i,j}+R_{i,j})}}{\sum_{x_{j} = 1}^{q}e^{\beta(S_{i,j}+T_{i,j}+R_{i, j})}}$$
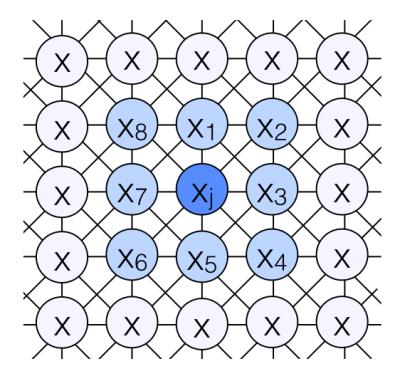
Where q is the requested number of classes, xNj describes the state of the neighboring pixels and β is a temperature parameter. The energy term Si,j counts neighboring pixels with matching class i to account for spatial correlation (Fig. 1), Ti,j measures how well the temporal profile matches the expected metabolite curve shapes and Ri,j incorporates information on metabolite area under the curve (AUC) ratios.
The spectral components form dimensions of a multivariate Gaussian conditional function:
$$p(y_{i,j}| x_{i,j})= \mathcal{N}( y_{i,j} |\bf{μ_{i}}, \Sigma_{i})$$
The eventual objective function to be minimized for the segmentation is given by:
$$Q_{\lambda} = -\sum_{i=1}^{q}\sum_{j=1}^{N}r_{i,j}log(p(y_{j}|x_{i,j})) + \lambda \sum_{i=1}^{q}\sum_{j=1}^{N} r_{i,j}log(\frac{ r_{i,j}}{p(x_{i,j}})$$
The parameter λ controls the degree of fuzziness5. The algorithm was tested and optimized on simulated 13C data and on the images from four rats with subcutaneously implanted tumors3.
Results
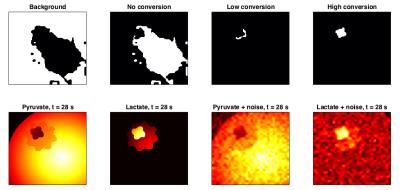
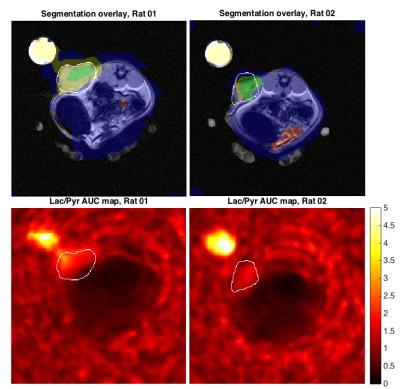
The MRF segmentation algorithm was able to detect the area of high pyruvate-to-lactate conversion when tested on in silico data, which had been corrupted with Gaussian noise prior to interpolation (Fig. 2). Applying the algorithm to the rat datasets showed it was able to detect the tumor in each case with no false positives, even in the presence of a lactate phantom (Fig. 3). The MRF segmentation provided a more accurate outline of the tumor than could be achieved by thresholding of simple parameter maps alone e.g. AUC ratio map.Conclusion
This work has shown that a novel fuzzy Markov random field algorithm can be used to segment 5D hyperpolarized 13C data; this is the first example of such an approach in hyperpolarized metabolic imaging. The performance of the algorithm has been shown using both in silico and in vivo data. In the future, the algorithm will be applied to human hyperpolarized data to automatically detect significant regions of altered metabolism that may be relevant in oncology, cardiology or neurology.Acknowledgements
No acknowledgement found.References
1. Albers, M.J., Bok, R., Chen, A.P., Cunningham, C.H., Zierhut, M.L., Zhang, V.Y., Kohler, S.J., Tropp, J., Hurd, R.E., Yen, Y.F. and Nelson, S.J., 2008. "Hyperpolarized 13C lactate, pyruvate, and alanine: noninvasive biomarkers for prostate cancer detection and grading. Cancer research", 68(20), pp.8607-8615.
2. Day, S.E., Kettunen, M.I., Gallagher, F.A., Hu, D.E., Lerche, M., Wolber, J., Golman, K., Ardenkjaer-Larsen, J.H. and Brindle, K.M., 2007. "Detecting tumor response to treatment using hyperpolarized 13C magnetic resonance imaging and spectroscopy", Nature medicine, 13(11), pp.1382-1387.
3. Daniels, C.J., McLean, M.A., Schulte, R.F., Robb, F.J., Gill, A.B., McGlashan, N., Graves, M.J., Schwaiger, M., Lomas, D.J., Brindle, K.M. and Gallagher, F.A., 2016. "A comparison of quantitative methods for clinical imaging with hyperpolarized 13C-pyruvate", NMR in Biomedicine.
4. Chatzis, S.P. and Varvarigou, T.A., 2008. "A fuzzy clustering approach toward hidden Markov random field models for enhanced spatially constrained image segmentation", IEEE Transactions on Fuzzy Systems, 16(5), pp.1351-1361.
5.Ichihashi, H., Miyagishi, K. and Honda, K., 2001, December. "Fuzzy c-means clustering with regularization by KL information", In Fuzzy Systems, 2001. The 10th IEEE International Conference on (Vol. 2, pp. 924-927). IEEE.
Figures