Synopsis

Metabolically inert hyperpolarized tracers can be used for perfusion measurements in vivo. In this work we present a simulation study to compare the performance for measurement of tissue perfusion of a conventional imaging approach to a segmented snapshot acquisition where each segment ends with a 90 degree RF pulse.

Introduction

The hyperpolarization of metabolically inert molecules provides unique possibilities for quantitative perfusion imaging¹. The magnitude of the hyperpolarized (HP) signal from such molecules provides a direct signal source that is virtually background-free and therefore not dependent upon the changes in the proton relaxation rates of tissues that underlie the quantification of physiological parameters in other methods of perfusion MRI. Furthermore, hyperpolarized MRI allows for the selection of imaging sequence parameters that can precisely control the observable signal of the perfusion agent in space and time. These acquisition parameters must be chosen very carefully since the HP signal is non-renewable and is depleted by RF excitation. A kinetic model for the evolution of the HP signal is therefore needed to evaluate and optimize imaging strategies for accurate and efficient quantification of tissue perfusion with HP agents in vivo².

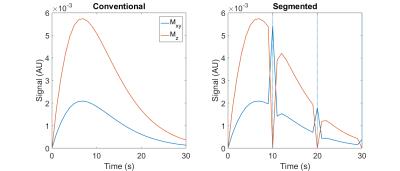
One unique advantage of HP MRI is the ability to expunge longitudinal magnetization within a slice with a 90 degree RF pulse. As Figure 1 shows, longitudinal magnetization may be replenished by delivery of fresh HP spins in blood, and one technique to exploit this potential is a segmented acquisition wherein a 90 degree pulse is applied at the end of each segment of repetitions. This technique may allow for improved measurements of perfusion parameters since the uncertainty in the amount of residual HP spins within the extravascular space immediately following a perfect 90 degree pulse is significantly reduced. Here we employ a kinetic model for perfusion imaging with HP agents to compare the performance of a conventional snapshot acquisition to the segmented snapshot acquisition described above.

Methods

Tissue perfusion was modeled using a two-compartment kinetic model with reversible exchange:

$$X \left( t \right) = e^{ A \left( t - \Delta \right) } v_e X_e \left( \Delta \right) + k_{ve} \int_{\Delta}^{t} e^{ A \left( t - \tau \right)} X_b \left( \tau \right) d \tau + v_b X_b \left( t \right)$$

$$A= - \left( \frac{k_{ve}}{v_e} + R_X \right)$$

$$M_{xy} \left( t + \delta \right) = M_z \left( t \right) \sin \left( \alpha \right) \propto X \left( t \right) \sin \left( \alpha \right)$$

$$M_{z} \left( t + \delta \right) = M_z \left( t \right) \cos \left( \alpha \right) \propto X \left( t \right) \cos \left( \alpha \right)$$

where X is the total amount of HP agent; X_e and X_b are the amounts of HP agent, and v_e and v_b are volume fractions for the extravascular and blood compartments, respectively; k_ve is the rate of spin exchange; R_X is the rate of HP spin loss to factors other than reverse exchange and RF excitation; M_xy and M_z are the transverse and longitudinal magnetizations, respectively; α is the RF tip angle; Δ is the time at which the previous RF excitation ends and δ is the RF pulse duration. This model is similar to the well-established extended Tofts model and models proposed previously for HP pyruvate², but without chemical exchange of HP spins.

The accuracy of estimates for k_ve, v_b and v_e was assessed for both acquisition strategies depicted in Figure 1 with a range of repetition times and flip angles by generating simulated HP time curves, adding a fixed level of noise and fitting the perfusion model to the noisy curves with these three perfusion parameters as fit parameters using a trust-region reflective method. Ground truth values of 0.02 s^-1, 0.09 and 0.2 were utilized for kve, vb and ve, respectively.

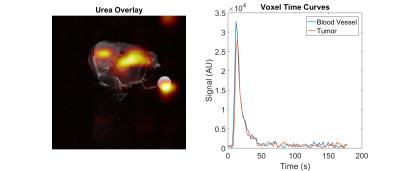
Within the kinetic model presented above, the VIF is assumed to be unperturbed by RF excitation, however when 90 degree pulses are applied to thick slices HP spins in major vessels may be lost, severely limiting the imaging window. We investigated this effect in an orthotopic mouse model of thyroid cancer by acquiring single-shot EPI images of HP ¹³C urea for a 1 cm slice covering the tumor and major vessels in the neck with a TR of 2 s and a flip angle of 90 degrees.

Results

Discussion & Conclusion

Acknowledgements

References

1. Ardenkjær-Larsen JH, et al. Increase in signal-to-noise ratio of > 10,000 times in liquid-state NMR. Proc Natl Acad Sci USA. 100(18), 10158-10163. doi:10.1073/pnas.1733835100 (2003).

2. Bankson, J. A. et al. Kinetic Modeling and Constrained Reconstruction of Hyperpolarized [1-13C]-Pyruvate Offers Improved Metabolic Imaging of Tumors. Cancer Res. 75, 4708-4717. doi:10.1158/0008-5472.CAN-15-0171 (2015).