3041
Improved reconstruction for IDEAL spiral CSI1Department of Electrical Engineering, Technical University of Denmark, Kgs. Lyngby, Denmark, 2MR Research Centre, Aarhus University, Aarhus, Denmark, 3GE Global Research, Munich, Germany
Synopsis
In this study we demonstrate how reconstruction for IDEAL spiral CSI (spectroscopic imaging scheme developed for hyperpolarized dynamic metabolic MR imaging) can be improved by using regularization with a sparsity constraint. By exploiting sparsity of the spectral domain, IDEAL spiral CSI can achieve chemical shift encoding by acquisition of only few time-shifted echoes. The minimum number of echoes required to avoid noise amplification can be decreased by means of regularization enforcing spectral sparsity, hereby reducing scan time. Improvements achieved by using regularized reconstruction are demonstrated for in vivo data from a hyperpolarized cardiac study of a pig.
Introduction
IDEAL spiral CSI1 is a spectroscopic imaging scheme developed for hyperpolarized dynamic metabolic MR imaging. The spectral-spatial encoding is based on a single-shot spiral, whereas the chemical shift encoding is based on echo-time shifting between excitations. Hereby, the sparsity of the spectral domain is exploited for faster imaging. To avoid noise amplifications in the reconstruction, a certain number of echoes is required. Here we propose, however, that noise amplification from acquiring less echoes can be decreased by using regularization with a sparsity constraint instead of using matrix inversion in the reconstruction. By acquiring less echoes, the individual image scan time is decreased, which can be utilized for better dynamic resolution or more slices in hyperpolarization studies.Methods
Figure 1 shows the spectral encoding scheme of IDEAL spiral CSI. The chemical shift encoding for the IDEAL scheme is:
$$y_{m,n} = \sum_q{E_{m,q}e^{i\omega_q t_n} \xi_q(\mathbf{k}_n)}$$
with $$$E_{m,q} = e^{i\omega_q TE_m}$$$, where $$$y_{m,n}$$$ is the measured data for the mth echo and the nth k-space sample and $$$\xi_q(\mathbf{k}_n)$$$ is the qth metabolite distribution in k-space. If $$$\mathbf{E}$$$ is well-conditioned, $$$\xi_q(\mathbf{k}_n)$$$ can be reconstructed by matrix inversion:
$$\xi_q(\mathbf{k}_n) = e^{-i\omega_q t_n} (\mathbf{E}^\dagger \mathbf{y}_n)_q$$
$$$\dagger$$$ denotes the Moore-Penrose pseudo-inverse. Saving scan time by acquiring less echoes, increases the condition number of $$$\mathbf{E}$$$, which leads to noise amplification when it is inverted. To limit this, the reconstruction can be regularized by enforcing a sparsity constraint using the L1-norm and by solving the minimization problem given by the following objective function:
$$\min_x ||\mathbf{E}\mathbf{x}_n - \mathbf{y}_n||_2^2 + \lambda ||\mathbf{x}_n||_1$$
where $$$\mathbf{x}_n = \xi_q(\mathbf{k}_n) e^{i\omega_q t_n}$$$, and $$$\lambda$$$ is a regularization parameter weighting the constraint enforced by the L1-norm. This reconstruction approach was implemented in the pre-existing IDEAL spiral CSI reconstruction pipeline iteratively for each k-space sample using fminsearch in Matlab. The regularization parameter was empirically selected to $$$\lambda$$$ = 100.000.
The method was demonstrated using in vivo data from a hyperpolarized [1-13C]pyruvate cardiac study of a healthy female Danish domestic pig weighing 30 kg. For the hyperpolarization experiment, the pig was first sedated with an intramuscular injection of Stressnil (2.0 mg/kg bodyweight) and Midazolam (0.1 mg/kg) and subsequently anaesthetized via continuous intravenous infusion of both Propofol (12 mg initial bolus dose, 0.4 mg/kg/h thereafter for maintenance) and Fentanyl for analgesia (8 µg/kg/h). The pig was intubated and mechanically ventilated (60 % O2-air mix) using a respirator system (GE Healthcare, Broendby, Denmark). A whole-body clinical 3T GE HDx MR scanner (GE Healthcare, Milwaukee, WI, USA) was used for imaging together with a bore-insertable 13C volume resonator (clamp shell design) integrated into the patient table for excitation (GE Healthcare, Milwaukee, WI, USA). Two arrays with 8 receive channels each2 were placed to cover the heart (Rapid Biomedical, Rimpar, Germany). The IDEAL spiral CSI was cardiac triggered with 4 excitations per trigger, 11 echoes, echo-time shifting of 0.9 ms, 12 excitations per image, and 8 image repetitions [TE/TR 1.1/100 ms, flip angle 15°, matrix 60x60, FOV 240x240 mm2, in-plane nominal resolution 4 mm, slice thickness 50 mm]. Data were averaged over the 8 repetitions before reconstruction.
Results
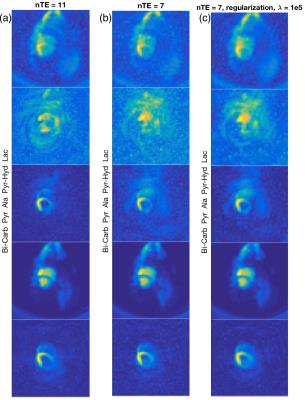
Figure 2 shows the reconstruction results from using all 11 echoes, using only 7 echoes with matrix inversion reconstruction, and from using 7 echoes with regularized reconstruction. The condition number of $$$\mathbf{E}$$$ was equal to 1.4 with 11 echoes and 2.8 with 7 echoes. The higher condition number is evident from the greater noise level in some of the metabolite images in Figure 2(b), especially for alanine and lactate. The relative error for using 7 echoes compared to 11 for matrix inversion reconstruction was 24 %. Figure 2(c) shows how the reconstruction using regularization is qualitatively improved in terms of less noise. This is supported quantitatively by means of a relative error of 19 %.Discussion
Using regularization in the IDEAL spiral CSI reconstruction can reduce noise amplification as demonstrated in the lactate images of Figure 2. Signal distribution in the pyruvate-hydrate images in Figure 2(a) was, however, not retrievable using regularization. In this study the regularization parameter $$$\lambda$$$ was empirically selected, but a more thorough investigation of parameter choice could potentially improve the reconstruction. Compared to matrix inversion in IDEAL spiral CSI a longer reconstruction time is expected.
Conclusion
Regularization of the IDEAL spiral CSI reconstruction can improve results, by reducing noise amplification from matrix inversion. This was demonstrated in vivo through qualitatively and quantitatively overall improved metabolite images. Shorter scan times can hereby be pursued with low penalty.Acknowledgements
This work has been partly funded by the Danish Council for Independent Research (DFF – 4005-00531) and the Danish National Research Foundation (DNRF124).References
1. Wiesinger F, Weidl E, Menzel MI, et al. IDEAL spiral CSI for dynamic metabolic MR imaging of hyperpolarized [1- 13C]pyruvate. Magn Reson Med. 2012;68(1):8-16.
2. Ringgaard S, Schulte RF, Tropp J, et al. 13C RF coil combination for cardiac and abdominal human and pig studies. In: Proc. Intl. Soc. Mag. Reson. Med. ; 2016:2152.
Figures