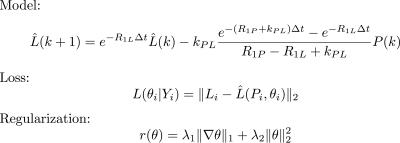3040

Spatio-temporally constrained reconstruction for hyperpolarized carbon-13 MRI using kinetic models

John Maidens¹, Jeremy W Gordon², Murat Arcak¹, Hsin-Yu Chen², Ilwoo Park², Mark Van Criekinge², Eugene Milshteyn², Robert Bok², Rahul Aggarwal³, Marcus Ferrone⁴, James B Slater², John Kurhanewicz², Daniel B Vigneron², and Peder EZ Larson²

¹Electrical Engineering & Computer Sciences, University of California, Berkeley, Berkeley, CA, United States, ²Radiology & Biomedical Imaging, UCSF, San Francisco, CA, United States, ³Medicine, UCSF, San Francisco, CA, United States, ⁴Clinical Pharmacy, UCSF, San Francisco, CA, United States

Synopsis

We present a method of generating metabolism maps from dynamic hyperpolarized carbon-13 MRI images. By incorporating prior information into our model-based reconstruction via spatial regularization of the parameter maps, we achieve two qualitative benefits: elimination of non-identifiability in unperfused background regions, and denoising. This method is illustrated on a simulated dataset and a clinical prostate cancer dataset.

Purpose

MRI using hyperpolarized carbon-13 is challenging due to the dynamic nature of the data collected, the low signal-to-noise ratio (SNR), and the difficulty of presenting large data sets consisting of dynamic spectroscopic images in an interpretable manner. Metabolism mapping by estimating parameters in a kinetic model from hyperpolarized MRI data has been shown to be useful for overcoming a number of these challenges.¹ Constraining the time evolution of signal in a given voxel to follow a kinetic model has been shown to allow map reconstruction from noisy, undersampled dynamic images, and to reduce the number of signal-depleting excitations required to generate images. Parameter mapping also facilitates interpretation of dynamic image data by summarizing spatial, temporal and spectral (i.e. chemical shift spectrum) information in a single spatial map.

Methods

Parameter maps are naturally a form of constrained reconstruction, as they constrain the data to lie on a manifold of trajectories of the kinetic model parameterized by the model parameters. This constrained reconstruction reduces the sequence of dynamic images to a single map by exploiting temporal correlations within the dynamic imaging data. Here we demonstrate that we can exploit spatial correlations in addition to temporal correlations by integrating prior information about the parameter map through regularization. Similar approaches have recently appeared for pharmacokinetic parameter mapping in dynamic contrast enhanced MRI.^2-4 Mathematically we formulate the constrained reconstruction as an optimization problem $$maximize\sum_{i\in S}L(\theta_i|Y_i)+r(\theta)$$ where the loss function L describes how well the model parameters θ_i fit the data Y_i collected from a single voxel i from the set S of all voxels, and r is a regularization term that enforces spatial structure assumed to be known a priori. The particular choices of loss function and regularization that we use in this work are given in Figure 1. We estimate parameter maps by minimizing the spatially regularized loss function using ADMM.⁵ This leads to an iterative reconstruction method that alternates between minimization of the individual loss functions for each voxel and a proximal mapping that depends on the spatial regularization. Using this method, the loss function minimizations become decoupled and can be performed in parallel, while the proximal mapping that couples the voxels can be computed quickly even for large matrix sizes^6,7 making this reconstruction algorithm efficient in practice.

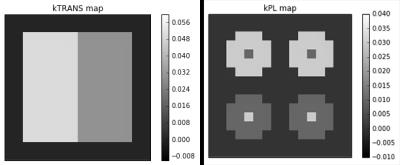
We validate our method using numerically simulated data and clinical data collected in prostate cancer studies. Simulated data are generated using the ground truth parameter maps shown in Figure 2, using the dynamical model described by Maidens et al..⁸ This process is repeated for different noise strengths, which correspond to signal-to-noise ratios of 8, 4, 2, and 1 in the voxel with the highest lactate signal. Clinical data were collected in an ongoing trial using a single shot EPI acquisition.⁹ [1-13C] pyruvate was polarized for 2 hours in a clinical polarized and the scan was started 5s after the end of injection. Pyruvate and lactate images were acquired in 16 8mm slices with a 8x8mm in-plane resolution (12.8x12.8cm FOV, 16x16 matrix size), at an effective 2s temporal resolution. Additional acquisition details are given in Gordon et al..¹⁰

Results & Discussion

In Figure 3 we show the results of our proposed spatially-constrained parameter mapping method on simulated data. We compare our proposed method with an alternative method for parameter mapping: independent voxel-wise mapping (equivalent to our method with no regularization) with a mask based on a perfusion threshold similar to the analysis by Larson et al..¹¹ We see that our method provides a substantial qualitative improvement in image quality across a range of noise levels. However it induces a slight quantitative bias (shrinkage) in model parameter estimates.In Figure 4 we illustrate the raw space/time/chemical data reconstructed from the EPI acquisition in a clinical prostate cancer study. In Figure 5 we show the result of our method. These results demonstrate that the addition of spatial regularization to model-based reconstruction provides two qualitative benefits: elimination of non-identifiability in unperfused background regions, and denoising. However, it does so at the expense of quantitative bias in the maps. Python code and data to reproduce these results are available at https://github.com/maidens/ISMRM-2017.

Conclusion

We have shown that constrained reconstruction via spatial regularization improves the qualitative performance of model-based parameter mapping. Looking forward, the ability to exploit spatial and temporal correlations in the data for denoising could potentially help to overcome problems with low SNR in hyperpolarized MRI, enabling the reconstruction of higher resolution images.

Acknowledgements

Research supported in part by NSERC postgraduate fellowship PGFD3-427610-2012 and NIH grants R01EB017449, R01CA183071 and P41EB013598.

References

1. Bankson JA, Walker CM, Ramirez MS, Stefan W, Fuentes D, Merritt ME, et al., Kinetic Modeling and Constrained Reconstruction of Hyperpolarized [1-13C]-Pyruvate Offers Improved Metabolic Imaging of Tumors. Cancer research, 2015; 75(22): 4708-4717.

2. Lingala SG, Guo Y, Zhu Y, Barnes S, Lebel RM, and Nayak KS, Accelerated DCE MRI using constrained reconstruction based on pharmaco-kinetic model dictionaries. Proceedings of the 23rd Annual Meeting of ISMRM, Toronto, Ontario, Abstract 1539, 2015.

3. Guo Y, Zhu Y, Lingala SG, Lebel RM, and Nayak KS, Highly accelerated brain DCE MRI with direct estimation of pharmacokinetic parameter maps. Proceedings of the 23rd Annual Meeting of ISMRM, Toronto, Ontario, Abstract 1093, 2015.

4. Guo Y, Lebel RM, Zhu Y, Lingala SG, Shiroishi MS, Law M, et al., High-resolution whole-brain DCE-MRI using constrained reconstruction: Prospective clinical evaluation in brain tumor patients. Medical Physics, 2016; 43(5): 2013-2023.

5. Boyd S, Parikh N, Chu E, Peleato B, and Eckstein J, Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning, 2011; 3(1), 1-122.

6. Barbero Á, and Sra S, Fast Newton-type methods for total variation regularization. Proceedings of the 28th International Conference on Machine Learning (ICML-11), 2011.

7. Barbero Á, and Sra S, Modular proximal optimization for multidimensional total-variation regularization. arXiv preprint arXiv:1411.0589, 2014.

8. Maidens J, Gordon JW, Arcak M, Larson PEZ, Optimizing flip angles for metabolic rate estimation in hyperpolarized carbon-13 MRI, IEEE Transactions on Medical Imaging, 2016; 35(11), 2403-2412.

9. Gordon JW, Vigneron DB, and Larson PEZ, Development of a Symmetric EPI Framework for Clinical Translation of Rapid Dynamic Hyperpolarized 13C Imaging. Magnetic Resonance in Medicine, 2016; DOI: 10.1002/MRM26123.

10. Gordon JW, Chen H-Y, Larson PEZ, Park I, Van Criekinge M, Milshteyn E, et al., Human Hyperpolarized C-13 MRI Using a Novel Echo-Planar Imaging (EPI) Approach, Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, Hawaii, USA, Submission #5415.

11. Larson PEZ, Gordon JW, Maidens J, Arcak M, Chen H-Y, Reed G, et al., Robust Quantitative Methods Applied to Clinical Hyperpolarized C-13 MR of Prostate Cancer Patients, Proceedings of the 24th Annual Meeting of ISMRM, Abstract 2347, 2016.

Figures

Figure 1: Model, loss function, and regularization used for parameter mapping. The model predicts the longitudinal magnetization in the lactate compartment $$$\hat L$$$ as a function of the pyruvate time series $$$P_i$$$, tissue parameters, and metabolic rate $$$\theta_i=k_{PL}$$$. The loss function for the metabolic rate $$$\theta_i$$$ and data $$$Y_i=(P_i,L_i)$$$ from voxel $$$i$$$ is given by the L2 norm of the difference between the observed and predicted lactate. The regularization combines a 3D total variation term and a Tikhonov regularization term. Nuisance parameters are fixed to the values $$$ R_{1P}=1/30$$$, $$$R_{1L}=1/30$$$. Hyperparameters $$$\lambda_1,\lambda_2$$$ are tuned by hand to achieve good performance.

Figure 2: Ground truth parameter maps used to generate simulated data. Slice through the central layer of the 3D parameter maps with matrix size 16x16x16. Left: rectangular region of high perfusion on the left bordering a rectangular region of low perfusion on the right. Right: large spheres of high and low metabolic activity in each of the two perfusion regions, surrounding a single-voxel feature of low and high metabolic activity respectively. This phantom is designed to test the robustness of metabolic parameter mapping methods to differences in perfusion, as well as their ability to reliably resolve large and small features.

Figure 3: Result of spatially-constrained reconstruction on simulated data. Our proposed spatially-constrained method is compared against an equivalent fit that treats all voxels independently. Qualitatively, we see that the spatial constraints lead to significantly-improved performance, particularly in the low SNR regime. However, it does so at the expense of a slight quantitative bias in the low perfusion region, where we see that the estimated metabolism parameter value is lower than in the high perfusion region.

Figure 4: Raw space/time/chemical data reconstructed from a clinical EPI acquisition in a subject with prostate cancer. Left: time series data at pyruvate and lactate frequencies corresponding to the voxel highlighted in red. Right: lactate data from 8 of the 16 slices at the time of the final acquisition t=42 seconds from the start of injection. The raw data is rather noisy and also difficult to interpret for metabolic activity due to 3D spatial, temporal and chemical dimensions. The bright voxels on the right of the images (see arrows) are due to a 13C urea phantom used for calibration.

Figure 5: Comparison of unconstrained and constrained parameter maps. The images on the top show parameter maps reconstructed using independent fit for each voxel, masked based on a minimum perfusion threshold computed based on the area under the pyruvate curve. We see sharp boundaries at the arbitrary cutoff, and numerous isolated pixels that surpassed the cutoff while all of their neighbours did not. On the bottom we show parameter maps reconstructed using spatially regularized estimate described in this paper. This method suppresses the background noise due to non-identifiability while maintaining realistic, smoothly-varying images.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

3040