Synopsis

Hyperpolarised [1-¹³C]pyruvate forms an effective probe of metabolism in vivo and has been used extensively to diagnose and prognosticate cancer. Commonly, [1-¹³C]pyruvate metabolism is quantified by either total metabolite-to-pyruvate integral ("AUC") ratios, or by fitting metabolic models by least-squares methods. Here, we use a modified Markov Chain Monte Carlo (MCMC) method with adaptive sampling and delayed rejection to fit models to hyperpolarised datasets of the healthy rat brain generated by a spectral-spatial EPI imaging sequence . The method is able to statistically discriminates between signal and noise, and returns quantitatively bounded maps of rate constants of interest, such as $$$k_{\text{Pyruvate}\rightarrow\text{Lactate}}$$$.

Purpose

Hyperpolarised [1-¹³C]pyruvate has heralded the birth of a new metabolic imaging modality.^[1] However, the datasets that the hyperpolarised pyruvate imaging techniques generate are high-dimensional and therfore suited to further analysis to estimate metabolic rate constants and reduce the dimensionality of the experiment. Commonly, analysis is performed by either integrating metabolites temporally, and taking the ratio of integrals; or by using least-squares methods to fit metabolic models. These methods are not robust,^[2],[3] e.g. integral ratios depend on the domain of integration, and least-squares methods are sensitive to (arbitrarily chosen) initial parameter values. Although several different multi-parametric models have been proposed for hyperpolarised datasets, few authors provide bounded estimates of fitted parameters.

We propose the use of Bayesian methods to analyse hyperpolarised datasets, which are able to quantitatively incorporate prior information and provide bounded estimates of rate constants. We use such methods to analyse lactate and pyruvate exchange in the healthy rat brain, imaged by spectral-spatial EPI.

Methods

DNP: [1-¹³C]pyruvate was polarised with OX63 (15mM) in a prototype hyperpolariser. After dissolution with NaOH, 1mL/80mM pre-polarised [1-¹³C]pyruvate was injected over 5 seconds.

Rodent experiment: A spectral-spatial-EPI sequence was used to image pyruvate metabolism to visible bicarbonate and lactate in the anaesthetised rat brain at 7T. RF Pulse: A 17-sublobe 6.8ms spectral-spatial RF pulse was designed as described previously;^[4] passband 400Hz, stop-band 2550Hz; thickness 6mm EPI Readout: Matrix 32×64, resolution 2×2×6mm³; TR=333ms/metabolite, TE=14ms. The acquisition order was pyruvate (FA=$$$15^\circ$$$), bicarbonate (FA=$$$90^\circ$$$), lactate (FA=$$$90^\circ$$$).

Data Analysis: The Delayed rejection Adaptive Metropolis (DAM)-MCMC algorithm^[5] was used to fit imaging data voxelwise to a two pool-model incorporating injection and decay:^[6]

\begin{align}S^{\text{Pyruvate}}(t)&=\begin{cases} 0&t<t_a\\ \frac{R_i}{k_\text{Pyr}}\left(1-e^{-k_\text{Pyr}(t-t_a)}\right)&t\in[t_a,\,t_e]\\ M_{\text{Pyr}}e^{-k_\text{Pyr}(t-te)}&t>t_e\end{cases}\end{align}

$$S^{X\neq\text{Pyruvate}}(t)=\begin{cases}0&t<t_a\\\frac{k_{\text{Pyr}X}\cdot{}R_i}{k_\text{Pyr}-k_X}\left[\frac{1-e^{-k_X(t-t_a)}}{k_X}-\frac{1-e^{k_\text{Pyr}(t-t_a)}}{k_\text{Pyr}}\right]&t\in[t_a,\,t_e]\\ \frac{M_{\text{Pyr}}\cdot{}k_{\text{Pyr}\,X}}{k_\text{Pyr}-k_X}\left[e^{-k_X(t-t_e)}-e^{-k_\text{Pyr}(t-t_e)}\right]+M_{X}e^{-k_X(t-te)}&t>t_e\\\end{cases}$$

where $$$S^{X}(t)$$$ is metabolite $$$X$$$ at time $$$t$$$, $$$R_i$$$ injection rate, $$$k_x$$$ pyruvate or metabolite $$$X$$$ decay rate, $$$MPyr$$$ maximum pyruvate signal; $$$t_a/t_e$$$ start/finish time of the injection, and $$$k_\text{PyrX}\equiv{}k_{\text{Pyr}\rightarrow\text{Lac}}$$$ the rate constant of interest.

This model is high-dimensional, but has previously been used in spectroscopic studies when fit via Levenberg-Marquardt.^[7,8] As the parameter landscape is multi-modal, with several local extrema, least-squares methods are not robust. In a Bayesian context, multi-modality dramatically reduces the efficiency of traditional MCMC methods,^[9] but Delayed Rejection schemes are well-suited to these high-dimensional multi-modal problems, maximising convergence rates.^[5,9]

Non-informative priors were used: the uniform distribution $$$[0,\infty]$$$ for all parameters except $$$t_a$$$ and $$$t_e$$$ which were constrained to lie in the interval of the duration of the experiment, $$$t_a,\,t_e\in[0,\,180\,\text{s}]$$$ and $$$t_e>t_a$$$. The fitting process required ~16GiB of RAM and 20 hours to complete; $$$n\approx5×10^{4}$$$iterations were required per voxel for convergence. If the chain did not converge, and/or the posterior distribution returned was uniform, the returned parameters were set to zero, masking the map according to temporal dynamics.

Results and Discussion

It was possible to resolve the production of hyperpolarised lactate and pyruvate, but not bicarbonate, in the healthy rat brain (Fig.1). The spatial profile of the surface coil was noted, and also a central bright voxel in both lactate and pyruvate images believed to co-localise with the middle cerebral artery (MCA).

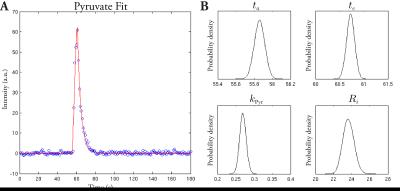
DAM-MCMC was able to robustly fit the model to the data. Representative posterior probability distribution functions (PDFs) are shown in Fig. 2, together with the fit in a single voxel. The algorithm masked the image based on the statistical properties of the signal timecourse. Returned PDFs were approximately Gaussian, matching the noise distribution of magnitude MR data acquired with SNR>2.^[10] The returned $$$ta$$$ and $$$te$$$ corresponded to the injection profile of the experiment.

Spatial maps of $$$k_{\text{Pyr}\rightarrow\text{Lac}}$$$ and $$$R_i$$$ were effectively deconvolved from initial signal modulation arising from the surface coil (Fig. 3). It was noted that $$$k_{\text{Pyr}\rightarrow\text{Lac}}$$$ was approximately homogeneous ($$$0.2\pm0.05\,\text{s}^{-1}$$$, mean±SD) over the volume of the brain, whilst $$$R_i$$$, believed to represent perfusion when interpreted spatially, was brightest in the location of the MCA and varied smoothly across the brain. Smoothness was not imposed in the model; neighbouring voxels were treated independently. This is believed to be consistent with $$$Ri$$$ reporting physiological perfusion of the rodent brain.

Conclusions

Acknowledgements

References

[1] Oliver J Rider and Damian J Tyler. “Clinical implications of cardiac hyperpolar- ized magnetic resonance imaging.” In: J. Cardiovasc. Magn. Reson. 15.1 (2013), p. 93.

[2] Helen J Atherton et al. “Validation of the in vivo assessment of pyruvate de- hydrogenase activity using hyperpolarised 13C MRS.” In: NMR Biomed. 24.2 (2011), pp. 201–8.

[3] Charlie J Daniels et al. “Quantitative analysis for hyperpolarized 13C-pyruvate imaging: comparison of methods on a clinical system.” In: Proc. Intl. Soc. Mag. Reson. Med. 23. 2015, p. 1887

[4] Angus Z Lau et al. “Spectral-spatial excitation for rapid imaging of DNP com- pounds.” In: NMR Biomed. 24.8 (2011), pp. 988–96.

[5] Heikki Haario et al. “DRAM: Efficient adaptive MCMC”. In: Stat. Comput. 16.4 (2006), pp. 339–354.

[6] Matthew L Zierhut et al. “Kinetic modeling of hyperpolarized 13C1-pyruvate metabolism in normal rats and TRAMP mice.” In: J. Magn. Reson. 202.1 (2010), pp. 85–92.

[7] Michael S Dodd et al. “In vivo mouse cardiac hyperpolarized magnetic resonance spectroscopy.” In: J. Cardiovasc. Magn. Reson. 15.1 (2013), p. 19.

[8] A.-M. L. Seymour et al. “In Vivo Assessment of Cardiac Metabolism and Function in the Abdominal Aortic Banding Model of Compensated Car- diac Hypertrophy”. In: Cardiovasc. Res. (Mar. 2015), pp. cvv101–.

[9] Miquel Trias, Alberto Vecchio, and John Veitch. “Delayed rejection schemes for efficient Markov-Chain Monte-Carlo sampling of multimodal distribu- tions”. In: (Apr. 2009), p. 32. arXiv: 0904.2207.

[10] John Geweke. “Evaluating the Accuracy of Sampling-Based Approaches to the Calculation of Posterior Moments”. In: Bayesian Stat. 4 (1992), pp. 169–193

[11] H Gudbjartsson and S Patz. “The Rician distribution of noisy MRI data.” In: Magn. Reson. Med. 34.6 (Dec. 1995), pp. 910–914