2932
Mapping the exchange kinetics of high-energy phosphates in the human calf muscle by direct 31P MRSI at 7T1Medical Physics in Radiology, German Cancer Research Center (DKFZ), Heidelberg, Germany
Synopsis
31P MRS allows the non-invasive observation of high-energy phosphate turnover in vivo. A model incorporating the effects of exchange processes onto the transverse steady-state magnetization was derived, which allows the direct estimation of relaxation rates from signal intensities in MRSI datasets. Multiple 31P MRSI datasets with different excitation parameters of four healthy were evaluated. Spatially-resolved turnover rates of high-energy phosphates could be estimated and are in agreement with literature values proving feasibility of the proposed approach.
Purpose
Phosphorus magnetic resonance spectroscopy(31P MRS) allows the non-invasive observation of high-energy phosphate turnover in vivo. Recently, Ren et al. showed that the underlying exchange kinetics are described by a multi-pool model1, which can be analyzed by saturation transfer(ST)2 or inversion transfer(IT) techniques. However, the prolonged signal preparations and measurement durations of these experiments prohibit incorporation into a MR spectroscopic imaging(MRSI) experiment for in vivo studies.
The purpose of this study was to demonstrate that the general relaxation properties of a coupled 31P spin system can be estimated directly by the detected steady-state magnetization that was generated in a 31P MRSI experiment.
Theory
In this study, we focused on the chemical exchange between phosphocreatine (PCr), the γ-phosphate of adenosine-5’-triphosphate (γ-ATP) and inorganic phosphate (Pi). Following the description given in Ref.[1], the matrix solution to the Bloch-McConnell equations is
$$M_z(t) = M_z^0-e^{At}(M_z^0-M_z(0)). [1]$$
For the assumed 3-pool model the actual and thermal z-magnetization vectors and the relaxation matrix are defined by
$$M_z = \begin{bmatrix}M_{PCr} \\M_{\gamma ATP} \\M_{P_i} \end{bmatrix},[2]$$
$$M_z^0 = \begin{bmatrix}M_{PCr}^0 \\M_{\gamma ATP}^0 \\M_{P_i}^0 \end{bmatrix},[3]$$
$$A = \begin{bmatrix} -( 1/T1_{PCr} + k_{PCr>ATP}) & k_{ATP>PCr} & 0 \\k_{PCr>ATP} & -( 1/T1_{\gamma ATP} + k_{ATP>PCr} + k_{ATP>Pi}) & k_{Pi>ATP} \\ 0 & k_{ATP>Pi} & -( 1/T1_{Pi} + k_{Pi>ATP}) \end{bmatrix}.[4]$$
1/T1 describes the intrinsic longitudinal relaxation rates and kPCr>ATP and kPi>ATP describe the pseudo first-order reaction rates of the creatine-kinase reaction and ATP hydrolysis. Repetitive radio-frequency(RF) excitation with flip angles
$$FA = \begin{bmatrix}\alpha_{PCr} & 0 & 0 \\0 & \alpha_{\gamma ATP} & 0 \\ 0 & 0 & \alpha_{Pi} \end{bmatrix} [5]$$
and repetition time TR result in the following steady-state of transverse magnetization:
$$M_{xy}^{ss}=sin(FA)\cdot \left[1-cos(FA)\cdot exp(A\cdot TR)\right]^{-1} \cdot \left[1-exp(A\cdot TR)\right]\cdot M_z^0 , M_{xy}^{ss}=\begin{bmatrix}M_{xy,PCr}^{ss} \\ M_{xy,\gamma ATP}^{ss} \\ M_{xy,Pi}^{ss} \end{bmatrix}.[6]$$
Measured transversal magnetization for different combinations of TR and FA are fitted to two models employing Eq.[6]: the 3-pool model (coupled fit of PCr, γ-ATP and Pi), yielding the parameters of the relaxation matrix A; the exchange-free model (separate fit of PCr, γ-ATP and Pi), yielding a diagonal matrix with apparent relaxation rates Rapp.
Methods
The calf muscle of four healthy volunteers (2female/ 2male, age:24-32) were measured on a MAGNETOM 7T (Siemens Healthineers, Erlangen, Germany) using a double-resonant 31P/1H volume coil (Rapid Biomedical, Rimpar, Germany). 31P MRSI was performed with a frequency-selective 3D 31P EPSI sequence (voxel size (15×15×40)mm³, 16×16×8 matrix, Δf=2000Hz, Tmeas=6–13min depending on number of averages). Multiple EPSI acquisitions (n=8–10) with different combinations of TR=[0.3–3.0]s and RF excitation schemes (α=[35–60]°, 4–ms sinc- or gaussian-shaped RF pulses) were used for the individual volunteers with total experimental durations ranging from 60-90 minutes. EPSI reconstruction and post–processing (Hamming–windowed k-space interpolation to a 32×32×16 matrix and application of 10Hz-Gaussian line broadening) was performed with a home-built MATLAB routine (The MathWorks, Natick, MA, USA). Signal intensities of localized 31P spectra were evaluated with the AMARES algorithm3 implemented in jMRUI4. These signal intensities of each voxel were fitted to the 3-pool and exchange-free model using the MATLAB optimization toolbox. The effective flip angles αi incorporated in Eq.[6] were calculated using a Bloch simulation.Results
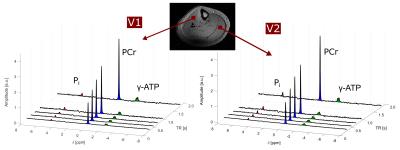
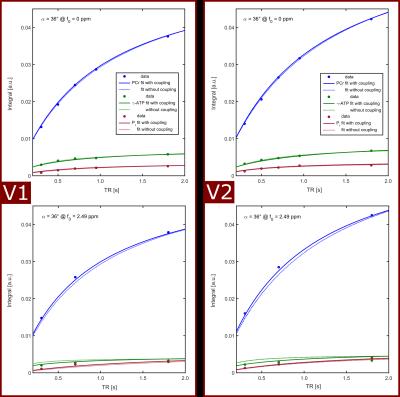
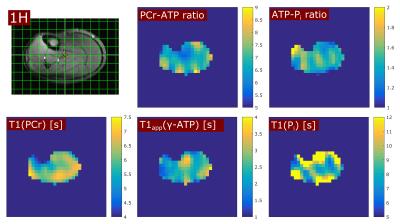
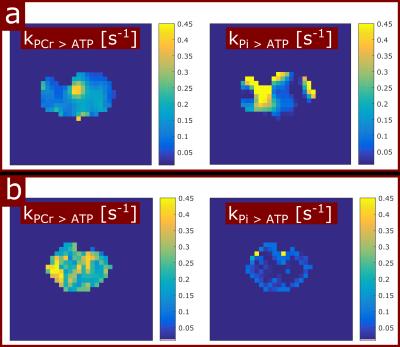
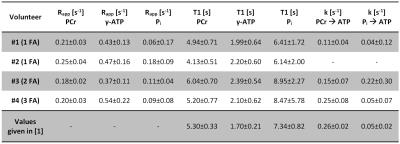
In all volunteers, the localized 31P spectra showed sufficient SNR for a reliable quantification of signal intensities of PCr, γ-ATP and Pi (Fig.1). Fig.2 illustrates the results of fitting the signal intensities from two exemplary voxels to the 3-pool and exchange-free model. Noise in the γ-ATP and Pi signal intensities mainly affected the robustness of 3-pool fitting. The values for M0 deduced from both models differed only slightly. The fits to the models of Eq.[6] yielded the parameters M0, Rapp, T1 and k for each voxel. Figure 3 displays maps of M0-ratios and T1 values of a transversal slice in volunteer #3. Exemplary maps for the reaction rates kPCr>ATP and kPi>ATP of volunteer #3 and #4 are shown in figure 4. Table 1 summarizes the mean values of relaxation parameters across a transversal slice of muscle tissue for all volunteers.Discussion & Conclusion
Comparison of the measured values given in Tab.1 to values reported in Ref.[1] are in good agreement. Nevertheless, the sensitivity to exchange processes of the proposed approach is reduced compared to ST or IT techniques. To improve the robustness of the 3-pool fit, acquisition of multiple FA and increased detection sensitivity for the Pi resonance are required, as was deduced from simulations with synthetized noisy 31P MRS datasets.
The presented data demonstrate that it is possible to probe relaxation mechanisms in a system of coupled spins directly by the transversal steady-state magnetization of a MRSI experiment. This allows spatially-resolved measurements of the exchange kinetics of high-energy phosphates by 31P MRSI without special signal preparation in experimental durations feasible for in vivo studies.
Acknowledgements
No acknowledgement found.References
1. Ren J, et al. Exchange kinetics by inversion transfer: Integrated analysis of the phosphorus metabolite kinetic exchanges in resting human skeletal muscle at 7 T. Magn. Reson. Med. 2015;73(4):1359–1369.
2. Shoubridge EA, et al. 31P NMR saturation transfer measurements of the steady state rates of creatine kinase and ATP synthetase in the rat brain. FEBS Lett 1982;140:289–292.
3. Vanhamme L, et al. Improved Method for Accurate and Efficient Quantification of MRS Data with Use of Prior Knowledge. J. Magn. Reson. 1997;129:35–43.
4. Naressi A, et al. Java-based graphical user interface for the MRUI quantitation package. Magn. Reson. Mater. Phys. Biol. Med. 2001;12:141–152.
Figures