2846

Volumetric Segmentation-Free Method for Quantitative Visualization of Cardiovascular Wall Shear Stress Using 4D Flow MRI

Evan M Masutani¹, Joseph Y Cheng², Marcus T Alley², Shreyas S Vasanawala², and Albert Hsiao¹

¹University of California, San Diego, La Jolla, CA, United States, ²Stanford University, Stanford, CA, United States

Synopsis

We demonstrate a volumetric technique for calculation and visualization of great vessel wall shear stress (WSS) from 4D Flow MRI data. Traditional methods for WSS have relied on planar sections of the data followed by explicit manual segmentation of vessel boundaries, which can be labor-intensive to perform. We propose a volumetric strategy for computation and visualization of WSS, which may facilitate its clinical translation.

PURPOSE

Wall shear stress is implicated in a variety of cardiovascular diseases, including atherosclerosis, aortic dissection, and aneurysm formation.^1-4 WSS is the drag force per area the endothelium exerts on luminal fluid. Cellular mechanotransducers may sense altered shear stress and actuate changes in vascular cell state.¹ It may therefore be beneficial to routinely evaluate wall shear stress in patients with cardiovascular disease. 4D Flow MRI has potential for enabling non-invasive in vivo measurement of WSS. Previous work has shown feasibility of calculation of WSS from 4D Flow MRI by calculating the numerical gradient of velocity at user-defined boundaries.⁵ Explicit manual demarcation of boundaries is cumbersome and potentially subjective.⁶ We present a method for calculation and visualization of WSS without manual segmentation to enable routine characterization of WSS, building on previous volumetric techniques.⁷

METHODS

With HIPAA-compliance and IRB approval, we identified three 4D Flow MRI acquisitions obtained as part of clinical imaging examinations at our institution. 4D Flow MRI was performed using a four-point encoded variable-density pseudo-randomly-ordered Cartesian sequence, followed by iterative compressed-sensing and parallel imaging reconstruction with respiratory self-navigation previously described.^8,9 Calculations of shear stress (τ) throughout the vector field was performed in MATLAB 2015b, shown in further detail in figure 1. Volumetric visualization was performed using the Arterys software (Arterys, San Francisco, CA). Spatial resolution ranged from [1.5-2.08 x 1.4-2.5 x 1.41-1.88 mm]. Temporal resolution ranged from [45 - 76 ms]. Acquisition times ranged from [11 – 13 mins]. We use a previously reported value of 3.2 mPa*sec for blood viscosity.⁵ Our primary assumption is that the gradient of velocity at the wall is approximately equal to the partial derivative of velocity with respect to the vessel wall unit normal. To reduce dimensionality to three spatial and one temporal dimensions for visualization, we compute the gradient of fluid speed using the Sobel operator and approximate the partial derivative for each dimension. To emphasize vascular boundaries for visualization, we employed a similar process for the anatomic 4D Flow data, and computed the Hadamard product of the signal intensity gradient magnitude and the original intensity data.

RESULTS

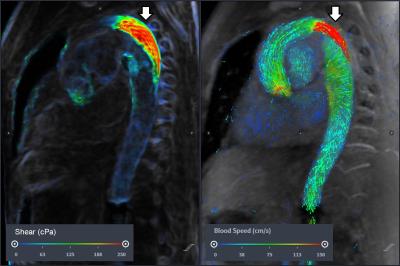
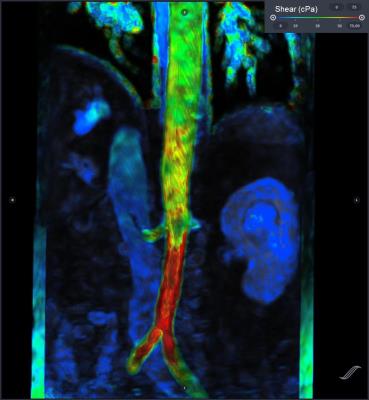
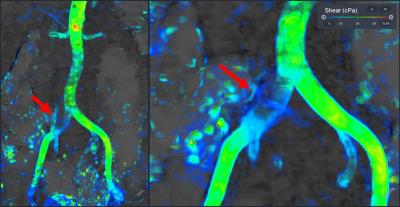
We present three examples of our algorithm to illustrate the ease and effectiveness of this approach. In a patient with aortic coarctation with severe stenosis, there is focally elevated WSS (>250 cPa) along the posterior wall of the distal arch (figure 2). The second example (figure 3) depicts WSS of the lower thoracic and abdominal aorta in a patient with presumed giant cell arteritis involving the abdominal aorta. The abdominal aorta exhibits locally elevated WSS (>200 cPa), due to abdominal aortic stenosis. In the third example, a focal right common iliac artery aneurysm demonstrates low WSS (figure 4). Outside of these regions, WSS during peak-systole is normal, approximately 40-60 cPa along the thoracic aorta and approximately 30-50 cPa along the abdominal aorta.^5,10

DISCUSSION

Regions of high and low WSS may contribute to the formation and evolution of aortic dissection and aneurysm. It has been hypothesized that locally high WSS may activate WSS-dependent vasodilatory and remodeling mechanisms.¹ The case of aortic coarctation presented here is suggestive that certain sections of the aortic wall may experience a greater tendency toward remodeling than others. It is worth noting that our estimates for WSS are similar to “normal” values reported in the literature.^5,10 Our method offers two potential advantages. First, the compressed-sensing 4D Flow implementation enables collection of higher resolution and higher signal-to-noise data, which may improve accuracy of estimates of WSS. Second, the implicit display of WSS eliminates potential mismatch between the fluid velocity boundary and user-defined boundaries for calculation of WSS.

CONCLUSION

We present a novel method to calculate and visualize WSS from 4D Flow MRI data, utilizing implicit rather than user-defined boundaries. This may enable greater accessibility of WSS for potential use in a clinical setting by removing the up-front need for manual segmentation, thus streamlining the computational process. Future work may include further refinement of the algorithm to account for vessel contractility, assessment of its sensitivity to acquired spatial resolution and application of the technique to study WSS in specific patient populations.

Acknowledgements

No acknowledgement found.

References

[1] Cunningham KS, Gotlieb AI. The role of shear stress in the pathogenesis of atherosclerosis. Lab. Invest. 2005;85:9-23.

[2] Bäck M, Gasser TC, Michel JB, Caligiuri G. Biomechanical factors in the biology of aortic wall and aortic valve diseases. Cardiovasc. Res. 2013;99(2):232-41.

[3] Macura KJ, Corl FM, Fishman EK, Bluemke DA. Pathogenesis in Acute Aortic Syndromes: Aortic Dissection, Intramural Hematoma, and Penetrating Atherosclerotic Aortic Ulcer. Am. J. Roentgenol. 2003;181(2):309-316.

[4] Cecchi E, Giglioli C, Valente S, Lazzeri C, Gensini GF, Abbate R, Mannini L. Role of hemodynamic shear stress in cardiovascular disease. Athersclerosis. 2011;214:249-256.

[5] van Ooij P, Powell AL, Potters WV, Carr JC, Markl M, Barker AJ. Reproducibility and Interobserver Variability of Systolic Blood Flow Velocity and 3D Wall Shear Stress Derived From 4D Flow MRI in the Healthy Aorta. J. Magn. Reson. Imaging 2016;43(1):236-248.

[6] Markl M, Wallis W, Harloff A. Reproducibility of Flow and Wall Shear Stress Analysis Using Flow-Sensitive Four-Dimensional MRI. J. Magn. Reson. Imaging 2011;33(4):988-94.

[7] Hsiao A, Lustig M, Alley MT, Murphy MJ, Vasanawala SS. Evaluation of Valvular Insufficiency and Shunts with Parallel-imaging Compressed-sensing 4D Phase-contrast MR Imaging with Stereoscopic 3D Velocity-fusion Volume-rendered Visualization. Radiology 2012;265(1):87-95.

[8] Vasanawala SS, Hanneman K, Alley MT, Hsiao A. Congenital heart disease assessment with 4D flow MRI. J. Magn. Reson. Imaging 2015;42(4):870-886.

[9] Cheng JY, Hanneman K, Zhang T, Alley MT, Lai P, Tamir JI, Uecker M, Pauly JM, Lustig M, Vasanawala SS. Comprehensive motion-compensated highly accelerated 4D flow MRI with ferumoxytol enhancement for pediatric congenital heart disease. J. Magn. Reson. Imaging 2016; 43: 1355–1368. doi:10.1002/jmri.25106

[10] Sughimoto K, Shimamura Y, Tezuka C, Tsubota K, Liu H, Okumura K, Masuda Y, Haneishi H. Effects of arterial blood flow on walls of the abdominal aorta: distributions of wall shear stress and oscillatory shear index determined by phase-contrast magnetic resonance imaging. Heart Vessels. 2016;31:1168-1175

Figures

Mathematical workflow for the proposed method. τ=shear stress, η=dynamic viscosity, v=velocity, n=unit normal to vessel wall, s=speed, I=3D MRI intensity data. We assume that wall shear stress is approximately equal to the gradient of fluid velocity at the boundary and evaluate the gradient numerically by using 3D Gaussian kernels with the Sobel operator. We process 3D MRI intensity similarly, but with the added step of solving for the Hadamard product of the magnitude of the intensity gradient and the original intensity data.

Computed wall shear stress (left) and blood flow (right) of the thoracic aorta during systole in a patient with aortic coarctation. The case is remarkable for stenosis at the aortic arch, with very high (>250 cPa) WSS posterior to stenosis. There is ectasia of the proximal descending aorta.

Computed WSS of the thoracic and abdominal aorta in a patient with vasculitis. WSS along the thoracic aorta during systole is approximately 40-60 cPa. Shear stress markedly increases in the infrarenal abdominal aorta, due to marked caliber change.

Computed WSS of the thoracic and abdominal aorta. WSS along the thoracic aorta during systole is approximately 40-60 cPa. This case is remarkable for aneurysm of the right common iliac artery; WSS along the wall of the aneurysm is reduced.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

2846