2826

An automatic method to estimate 3D Pulse Wave Velocity from 4D-flow MRI data
Joaquin Mura1, Julio Sotelo1, Cristian Montalba1, Bram Ruijsink2, David Nordsletten2, Reza Razavi2, Pablo Irarrazaval1,3, Cristian Tejos1,3, Marcelo Andia1,4, and Sergio Uribe1,4

1Biomedical Imaging Center, Pontificia Universidad Catolica de Chile, Santiago, Chile, 2Department of Biomedical Engineering, King's College London, London, United Kingdom, 3Department of Electrical Engineering, Pontificia Universidad Catolica de Chile, Santiago, Chile, 4Department of Radiology, School of Medicine, Pontificia Universidad Catolica de Chile, Santiago, Chile

Synopsis

One of the most common and well-accepted biomarkers for Cardiovascular diseases is the Pulse Wave Velocity (PWV), related with the time-shift observed in pressure or flow waveforms along the artery. Some drawbacks in its application can be summarized as data often collected by catheterization or separated 2D flow planes, centerlines do not necessarily coincide with the path followed by wavefronts and, the methods are user-dependent. We propose a novel method for PWV avoiding centerlines by evaluating flows over wavefronts to improve results. A systematic analysis of phantom scans and to a set of volunteers and patients show promising results.

Purpose

Accurate assessment of risk factors in Cardiovascular diseases are crucial to determining whether further treatments or interventions are necessary. A clinical biomarker is PWV, obtained from calculating the shift in pressure of flow waveforms. Pressure waveforms can be obtained from cardiac catheterization, an invasive measurement not free of complications. Flow evaluations1,2, although effective and reliable, may require many observation points as suggested in3, at expenses of less cardiac phases. One key observation for accurate evaluations of PWV is that in curved arteries, the propagation of waves does not follow planes perpendicular to some symmetry axis, but intricate wavefronts that strongly depends on the arterial morphology. We introduce a novel method to automatically estimate continuous 1D PWV and projected to 3D, from velocities acquired with 4D-flow MRI data.

Methods

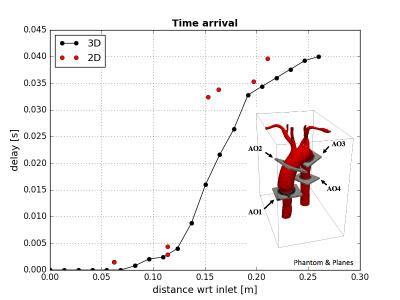
In order to tackle this problem, we solve the distance equation (known as Eikonal equation, see figure 1) in segmented geometries by applying the Fast-Sweeping method for unstructured meshes4. The outcome is a map of the region of interest revealing approximated wavefronts along the artery (since distance do not exactly match -but it is close to- the pulse arrival time), used to calculate local averages of flows with a lower variance to ensure accurate evaluations from 4D-flow data. Once selected a number of isosurfaces from the distance map, we obtain normalized flow waveforms, as in figure 2, used to evaluate the time-delay of PWV along the artery through cross-correlation analysis between one reference curve with respect to the others. Hence, we calculate slowness = 1/PWV = slope of time-delay curve. The latter is obtained by applying linear regressions locally in the curve, due to their sensitivity to noise. Note that slowness is used instead of PWV directly since we may obtain very short delays (almost zero) in some regions. Hence, once obtained the 1D PWV representation, by using the same distance map, we perform the extrapolation of PWV to 3D morphologies in order to facilitate clinical evaluation.

Results

In figure 2, the PWV map estimated in realistic phantom5 from 4D-flow data, using an MR Phillips Achieva 1.5T. The 4D-flow data was collected in three different days (namely I,II,III), and in each one we acquired three different resolutions (namely Low-Res, Med-Res and Hi-Res), showing excellent agreement each other, with a maximum difference below 5% near the section marked with the red line (Figure 2e). We have selected 20 isosurfaces in our evaluations. It can be noticed that appears the stiff tube in blue color, while in the aortic arch it is softer. We must remark that in the case of this phantom, the exact PWV in the tube near the inlet cannot be accurately estimated since there the waves propagates too fast to capture significant variations in cross-correlations with respect to the inlet waveform. Therefore, we have imposed 1/40 [s/m] as the lower limit to slowness to avoid divisions by zero in the calculation of PWV. We also test our method in a set of three volunteers and three Fontan patients, corresponding to figures 3 (a) and (b), respectively. While similar results are obtained in healthy volunteers, where values are between 1 and 8 [m/s], relevant differences can be observed near the aortic arch, where it is expected a stiffer region due to the effect of Fontan disease. On the same patients, several artifacts were observed downstream, mostly due to the movement during the acquisition, since Fontan patients are below 12 years, producing some alterations in our results. In figure 4, we show a preliminary comparison between 2D-flow data collected in four slices, where our method shows a good agreement with the data.

Discussion and Conclusion

We present a fast and non-invasive method to estimate PWV in complex geometries. Although preliminary results are quite promising, further validations are still needed. Special attention has to be paid in the determination of the first time arrival since the delay calculated using cross-correlations must increase along the artery, which may fail in evaluations close to the reference isosurfaces or due to noisy data. The application of linear regressions to estimate slopes in time-distance diagrams has been fundamental to deal with realistic inputs. In future developments, we will apply forth and back cross-correlations, as well as an iterative method to recover full 3D PWV considering also local cross-correlations to improve this method.

Acknowledgements

We thanks to CONICYT - PIA - Anillo ACT1416, CONICYT FONDEF/I Concurso IDeA en dos etapas ID15|10284, and FONDECYT #1141036 grants. Sotelo J. thanks to the School of Engineering, Pontificia Universidad Catolica de Chile, for his Post-Doctoral Fellow.

References

1. Boese JM, Bock M, Schoenberg SO, Schad LR, “Estimation of aortic compliance using magnetic resonance pulse wave velocity measurement”. Phys Med Biol. 2000 Jun; 45(6):1703-13.

2. Grotenhuis HB, Ottenkamp J, Fontein D, Vliegen HW, Westenberg JJ, Kroft LJ, de Roos A, “Aortic elasticity and left ventricular function after arterial switch operation: MR imaging--initial experience”. Radiology. 2008 Dec; 249(3):801-9.

3. Kröner ES, van der Geest RJ, Scholte AJ, Kroft LJ, van den Boogaard PJ, Hendriksen D, Lamb HJ, Siebelink HM, Mulder BJ, Groenink M, Radonic T, Hilhorst-Hofstee Y, Bax JJ, van der Wall EE, de Roos A, Reiber JH, Westenberg JJ, “Evaluation of sampling density on the accuracy of aortic pulse wave velocity from velocity-encoded MRI in patients with Marfan syndrome”. J Magn Reson Imaging. 2012 Dec; 36(6):1470-6.

4. Qian J, Zhang YT, Zhao HK, “Fast sweeping methods for Eikonal equations on triangular meshes”. SIAM J. Numer. Anal. 2007; 45(1):83-107.

5. Urbina J, Sotelo JA, Springmüller D, et al. Realistic aortic phantom to study hemodynamics using MRI and cardiac catheterization in normal and aortic coarctation conditions. J Magn Reson Imaging. 2016 Sep;44(3):683-97

Figures

Figure 1: First steps in the proposed method. Starting from a time sequence of velocity fields in the segmented mesh denoted $$$\Omega$$$ (a), we use the Eikonal solver to obtain the distance map with respect to the inlet determined by the nodes lying on the reference surface $$$\Gamma$$$ (b). Then, using a set of isosurface from figure (b) $$$d=constant$$$ distributed along the artery, it is calculated the flow over each isosurface, obtaining waveforms as shown in (c). Preliminary results show a reduction in about 40% of the variance using distance isosurfaces in (b) instead of planes.

Figure 2: The normalization of curves in Fig.1c yields a waveform diagram (a). Time delay along the arterial path is estimated from cross-correlations (b). The slopes in this curve provide an estimation of the slowness, corresponding to 1/PWV. In the case of the phantom, three different day measurements (I,II and III) were tested using approximately the same input flow (c). The estimated 1D PWV is in (d), and the extrapolation to 3D is obtained (e). Note that the phantom is clamped at the inlet and at the lower outlet and the upper branches were not considered.

Figure 3: Three volunteers (a) and three patients with Fontan disease were scanned in MR Phillips Achieva 1.5T with resolutions of 2.5x2.5x2.5 [mm] (a) and 2.1x2.1x2.1 [mm] (b), respectively. The set of volunteers presents similar results, with PWV varying between 1 and 8 [m/s]. In the ascending aorta of patients, Fontan disease alters the physiology inducing stiffer walls, as observed. Alterations in descending aorta are due to movement. The full method takes approximately 10 seconds for each case on a desktop computer (Intel i7, 3.46 Mhz, 32GB RAM), where meshes are composed of approximately 6100 nodes and 23,000 tetrahedrons.

Figure 4: Comparison in the first-time arrival (or time-delay) using our 3D (black line) method and 2D flow (red dots) acquired in planes marked as AO1, AO2, AO3, and AO4. The distance between planes was calculated from the arc length of a manually constructed centerline. We recall that the inverse of the slope leads us the estimation of PWV.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
2826