Synopsis

Dixon imaging has recently been shown to be useful in contrast-enhanced MR angiography due to motion robustness and improved signal-to-noise ratio. Single-echo Dixon mostly avoids the time penalty associated with multi-echo Dixon imaging, but may incur some time penalty when choosing an echo time to give optimal signal-to-noise ratio (SNR). For dynamic scans, it is beneficial to optimize the imaging parameters for speed, even at the expense of SNR. Additionally, signal contrast can be optimized to further suppress the background water signal. The purpose of this work is to describe optimization of SNR and signal contrast for single-echo Dixon imaging.

Purpose

The Dixon method of water-fat imaging uses the chemical shift induced phase offset between water and fat signals to produce separate water-only and fat-only images. This method can allow for the improved visualization of water structures within fat, and fat signals within water. Additionally, Dixon imaging has been shown to be useful in contrast-enhanced MR angiography due to motion robustness¹ and improvement in signal-to-noise ratio². There is a time penalty associated with multi-echo Dixon techniques, however, either from using multiple repetitions to acquire images at different echo times or lengthening the repetition time to perform a multi-echo acquisition.

Single-echo Dixon mostly avoids the time penalty associated with dual-echo Dixon imaging, but may incur some time penalty when choosing an echo time to give optimal signal-to-noise ratio (SNR) of the real-valued water and fat images. The SNR of single-echo Dixon images is optimal when water and fat are $$$\pm\pi/2$$$ out of phase, which corresponds to echo times of TE=1.7ms and TE=2.8ms at 3.0T. To keep scan times short, it is often beneficial to choose TE=1.7ms. However, due to system limitations, low bandwidth, or long readout durations, the shorter echo may not be an option and the longer (TE=2.8ms) must be used. For dynamic scans, such as time-resolved single-echo Dixon CE-MRA, it is advantageous to reduce the repetition time so that image update times can be as short as possible. In this case, it is beneficial to optimize the imaging parameters for speed, even at the expense of SNR.

Additionally, when contrast-enhanced single-echo Dixon imaging is used in place of the more traditional time-subtraction method of background suppression, there remains subtle background water signal in the images. While this contextual anatomy can be useful, system parameters may be chosen to maximize the difference, or signal contrast, between the contrast-enhanced signal and the background signal. The purpose of this work is to describe the space of system parameters for optimization of SNR and signal contrast for single-echo Dixon imaging and provide insight into choosing optimal parameters.

Theory

The SNR of single-echo Dixon has previously been extensively studied theoretically in comparison to the SNR of time-subtraction CE-MRA². Here, the SNR is normalized with respect to the SNR of a baseline (subscript "0") single-echo Dixon acquisition with chemical shift-induced phase $$$\theta_0=2\pi\Delta{f}(TE_0)$$$ and readout bandwidth $$$BW_0$$$. This normalized SNR equation is shown in Equation 1.

$$relSNR=\frac{|sin(\theta)|}{|sin(\theta_0)|}\sqrt{BW_0/BW}\hspace{1cm}\text{(Eq. 1)}$$

For dynamic single-echo Dixon imaging, the goal is to maximize the SNR while minimizing the repetition time.

To maximize the signal contrast between tissues, the difference between the signal calculated from the spoiled gradient echo signal equation is used (Equation 2).

$$\Delta{S}=S_2-S_1=sin{\alpha}\frac{1-e^{-\frac{TR}{T1_2}}}{1-\cos{\alpha}e^{-\frac{TR}{T1_2}}}-sin{\alpha}\frac{1-e^{-\frac{TR}{T1_1}}}{1-\cos{\alpha}e^{-\frac{TR}{T1_1}}}\hspace{1cm}\text{(Eq. 2)}$$

where $$$T1_1$$$ and $$$T1_2$$$ are the longitudinal relaxation times of two different tissues, and $$$\alpha$$$ is the flip angle. This equation can be maximized with respect to $$$\alpha$$$ using an approximate solution of the cubic³ or with a numerical solver.

Results

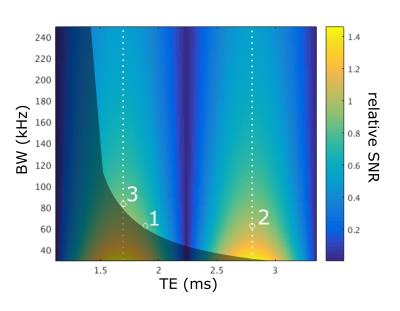
Figure 1 shows a plot of the relative SNR as a function of both echo time and bandwidth (note that $$$\theta$$$ is lineraly related to echo time), normalized to $$$BW_0$$$=$$$\pm$$$62.5 kHz and $$$TE_0$$$=1.884ms. The dotted lines indicate optimal SNR for all bandwidths, while the greyed area indicates the approximate area of unattainable echo times due to system limitations. Note that along a single bandwidth, the SNR varies according to $$$|sin{(\theta)}|$$$ as previously reported².

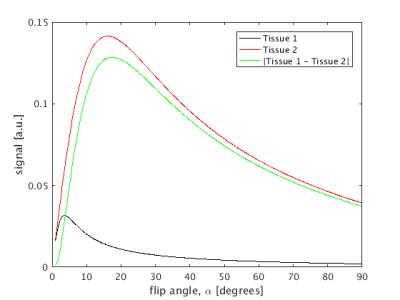
Figure 2 shows a plot of signal resulting from tissues with $$$T1_1=2000$$$ms and $$$T1_2=100$$$ms varying as a function of $$$\alpha$$$ with $$$TR=4$$$ms. The green line indicates the absolute difference between the signals, and the peak indicates the flip angle, $$$\alpha$$$ that gives maximum contrast - in this case 17.4 degrees.

Discussion

In Figure 1, point 1 is considered the baseline single-echo Dixon acquisition (TE=1.884, BW=±±62.5kHz). By moving to point 2 (TE=2.8ms) the SNR is improved, but TR is also increased. For dynamic single-echo Dixon imaging, it may be advantageous to move to point 3 (TE=1.7ms, BW=±83.33kHz) which has a shorter TR than point 2, and higher SNR than point 1.

Moving from point to point in the SNR space may change the TR, and in turn change the optimal flip angle. By alternating between optimizing SNR and signal contrast, a solution optimizing both can be found.

This work has described the theory for optimization of SNR and signal contrast for single-echo Dixon imaging, allowing improved image quality of single-echo Dixon images while reducing the image update time of a dynamic single-echo Dixon scan.

Acknowledgements

References

1. Leiner T. Eur Radiol 2013;23:2228

2. Stinson EG. MRM 2015;74:81.

3. Pelc NJ. MRM 1993;29:695.