2797
Unenhanced Peripheral MRA with Robust Background Suppression using Chemical-Shift-Encoded Single-Slab 3D GRASE: Decomposition of Angiogram and Fatty Backgrounds1Department of Biomedical Engineering, Sungkyunkwan University, Suwon, Korea, Republic of, 2Center for Neuroscience Imaging Research, Institute for Basic Science (IBS), Suwon, Korea, Republic of
Synopsis
Unenhanced peripheral MRA, which is based on cardiac-gated fresh blood imaging, exploits a pulsatile nature of arterial blood flow to differentiate arteries from veins and stationary backgrounds by subtracting two sets of images in cardiac diastole and systole, respectively. However, background signals remain substantial after subtraction due to either varying R-R intervals in between the two cardiac phases or subject motion, potentially obscuring the delineation of angiograms. Under the hypothesis that most of bright background signals result from fatty tissues, we develop a novel, unenhanced peripheral MRA method with robust background suppression using chemical-shift-encoded single-slab 3D GRASE to decompose angiograms and fatty background tissues directly from the subtracted, undersampled k-space data between the dual cardiac phases under the framework of compressed sensing.
Introduction
Unenhanced peripheral MRA, which is based on cardiac-gated fresh blood imaging (1), exploits a pulsatile nature of arterial blood flow to differentiate arteries from veins and stationary backgrounds by subtracting two sets of images in cardiac diastole and systole, respectively. However, background signals remain substantial after subtraction due to either varying R-R intervals in between the two cardiac phases or subject motion, potentially obscuring the delineation of angiograms. Under the hypothesis that most of bright background signals result from fatty tissues, we develop a novel, unenhanced peripheral MRA method with robust background suppression using chemical-shift-encoded single-slab 3D GRASE to decompose angiograms and fatty background tissues directly from the subtracted, undersampled k-space data between the dual cardiac phases under the framework of compressed sensing. Simulations and experiments suggest that the proposed method clearly separates angiograms from fatty background tissues and enhances the delineation of small arteries even at high reduction factors.Cardiac-Gated, Chemical-Shift-Encoded Single-Slab 3D GRASE
A schematic and timing diagram of the proposed, cardiac-gated chemical-shift-encoded single-slab 3D GRASE pulse sequence is shown in Figure1. Data acquisition is performed twice during cardiac systole and diastole. The proposed pulse sequence is designed to achieve the shortest possible echo spacing that can accommodate triple asymmetric echoes in between neighboring refocusing RF pulses while producing an optimal SNR for chemical shift encoding. To this end, as suggested in (2) for reliable fat-water separation over all combinations of the two components in a voxel, the center echo is shifted from the SE point such that the corresponding phase difference between fat and water is set to pi/2. The phase shift in the echo direction is then separated by 4pi/3, leading to -5pi/6, pi/2, and 11pi/6 relative to the SE point. To slow down relaxation induced single decay, and elongated echo trains, variable-flip-angles are calculated using inverse solution of the Bloch equations. Phase encoding blips randomly spread signals along echo direction to promote sufficient incoherence. Phase errors caused byalternating readout gradient polarities are estimated from projection data acquired from phase correctionpre-scan.
Decomposition of Angiograms and Fatty Backgrounds
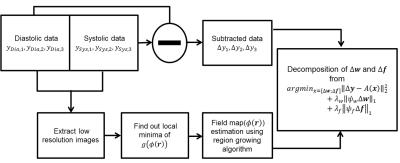
Chemical-shift-encoded residual in each echo, which results from subtraction between cardiac systole and diastole data, is described by the following model that includes angiogram and fatty background tissues: $$ \Delta \rho_l = ( \Delta w + \Delta f \sum_{m=1}^N \alpha_m e^{2\pi i \psi_m t_l } )e^{2\pi i \phi t_l} $$ where $$$ \Delta \rho_l = \rho_{dia,t_l} - \rho_{sys,t_l} $$$, $$$\rho $$$ is voxel signal, $$$ t_l $$$ is echo time , $$$ \Delta w$$$ is angiogram , $$$ \Delta f $$$ is fatty background, $$$\alpha_m $$$ is relative amplitude of fat peaks, $$$\psi_m $$$ is chemical shift for each peak, and $$$\phi $$$ is field map. The signal model including undersampling in k-echo space:$$ \Delta y_l = \mathcal F_u\left\{ ( \Delta w + \Delta f \sum_{m=1}^N \alpha_m e^{2\pi i \psi_m t_l } )e^{2\pi i \phi t_l} \right\}$$ where $$$ \Delta y_l =y_{dia,t_l} - y_{sys,t_l} $$$.
In the matrix form : $$g(x (r))=\begin{Vmatrix} \begin{bmatrix} e^{2\pi i \phi (r) t_1} & 0 & 0 \\ 0 & e^{2\pi i \phi (r) t_2} & 0 \\ 0 & 0 & e^{2\pi i \phi (r) t_3} \end{bmatrix} \begin{bmatrix} 1 & \sum_{m=1}^N \alpha_m e^{2\pi i \psi_m t_1} \\ 1& \sum_{m=1}^N \alpha_m e^{2\pi i \psi_m t_2} \\ 1& \sum_{m=1}^N \alpha_m e^{2\pi i \psi_m t_3} \end{bmatrix} \begin{bmatrix} \Delta w \\ \Delta f \end{bmatrix} - I(r)\end{Vmatrix}_2^2$$ where $$$x (r) $$$ is$$$\begin{bmatrix} \Delta w \\ \Delta f \end{bmatrix}$$$ and $$$ I(r) = \begin{bmatrix} \mathcal F^{-1}(y_{t_1}) &; \mathcal F^{-1}(y_{t_2}) &; \mathcal F^{-1}(y_{t_3}) \end{bmatrix} $$$, $$$ y_{t_l} $$$ is cardiac systole or diastole data
After substituting the vector $$$ \begin{bmatrix} \Delta w \\ \Delta f \end{bmatrix} $$$ with its least squares estimate, signal model can be represented in terms of the field map.
Fieldmap estimation is performed by applying the region growing algorithm(3) from the local minima of $$$g(\phi (r))$$$.
Given the fieldmap, unconstrained linear optimization problem is formulated :
$$ \underset{x=[\Delta w;\Delta f]}{\operatorname{argmin}} {\lVert \Delta y -A(x) \rVert}_2^2+\lambda_w {\lVert \psi_w \Delta w \rVert}_1+\lambda_f{\lVert \psi_f \Delta f \rVert}_1 $$
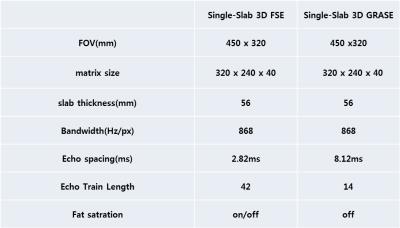
where $$$ \psi_w, $$$and $$$ \psi_f, $$$ are wavelet transform, and $$$ \lambda_w$$$and $$$ \lambda_f $$$ are regularization parameters for each regularization term. A flow chart of image reconstruction is shown in Figure2. Experimental imaging parameters are descripted in Figure3.
Result
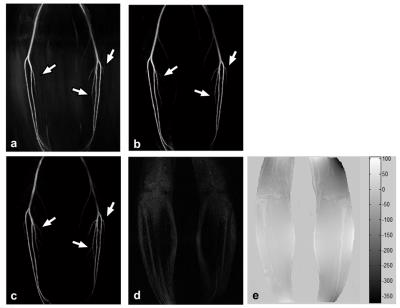
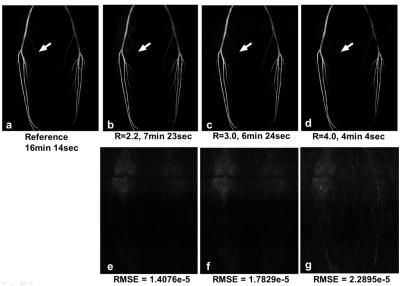
Figure4 shows the calf images, as compared to conventional methods, the proposed method provides robust background tissue suppression and detailed delineation of angiogram. With increasing reduction factor, noise amplification interrupts depiction of small arteries (Fig5).Conclusion
The proposed cardiac-gated chemical-shift-encoded single-slab 3D GRASE clearly separates angiograms from fatty background tissues and enhances the delineation of small arteries even at high reduction factors.Acknowledgements
This work was supported by IBS-R015-D1 and ICT&Future Planning (2016M3C7A1913844).
References
[1] Miyazaki M, Takai H, Sugiura S, Wada H, Kuwahara R, Urata J. Peripheral MRangiography: Separation of arteries from veins with flow-spoiled gradient pulses inelectrocardiography-triggered three-dimensional half-Fourier fast spin-echo imaging. Radiology 2003; 227: 890-896.
[2] Pineda AR, Reeder SB, Wen Z, Pelc N J. Cramer rao bounds for three-point decomposition of water and fat. Magn Reson Med 2005; 54: 625-635.
[3] Wenmiao Lu, Brian A. Hargreaves. Multiresolution Field Map Estimation Using Golden Section Search for Water-Fat Separation. Magn Reson Med 2008; 60:236-244.
Figures