Synopsis

Cardiac MR-Elastography has significant potential to provide a non-invasive measure of myocardial tissue health. A core challenge in its application is the substantial motion of the heart over the cardiac cycle, which introduces a bias in the quantified apparent stiffness. In this work we apply a reconstruction technique for MRE designed to correct changes in apparent stiffness due to deformation. The reconstruction method is tested on anatomically accurate homogeneous and heterogeneous heart phantoms that are inflated to mimic diastolic function. The results demonstrate the ability of the reconstruction technique to retrieve intrinsic stiffness values, even under substantial inflation.

Introduction

Assessing the health of myocardial tissue has been a field of significant research interest, as structural tissue alterations are intrinsically linked to a range of cardiac conditions¹. While several techniques have been employed for evaluating tissue health, they often rely on invasive pressure measurements (pressure-volume analysis²), biopsy, or require a significant amount of non-invasive data (patient-specific modelling³). An alternative for characterising tissue biomechanical properties is with MR-Elastography (MRE), an imaging technique using shear waves propagation to infer stiffness⁴. Analysing MRE wave images enables the reconstruction of fundamental viscoelastic properties, as the wave behaviour is affected by local tissue structure. While MRE has been successfully applied in studies of the liver⁵ and breast cancer⁴, the complex cardiac function and structure have limited its use in the heart. The dynamic change in stiffness between the passive and active states, the structural anisotropy as well as regional stiffness alterations in pathological hearts, complicate the interpretation of the mechanical properties based on wave behaviour. Particularly, the substantial cardiac motion over the cycle introduces a bias in the apparent stiffness⁶, by conflating effects of deformation and geometry with tissue properties and limiting its clinical specificity.

In this work we exploit a reconstruction technique aimed at correcting apparent stiffness alterations due to changes in deformation state⁷. The technique is tested over experiments with anatomically accurate homogeneous and heterogeneous heart phantoms mimicking the diastolic filling function. Viscoelastic properties are measured in reference and inflated states, illustrating the change in apparent stiffness as well as the ability of the proposed method to recover the unbiased intrinsic stiffness properties.

Methods

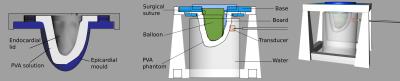
The phantoms were based on the end-systolic geometry of the left ventricle of a healthy volunteer. Phantoms were made of polyvinyl alcohol (PVA) cryogel, a material used to mimic soft biological tissues⁸. Following a typical experimental procedure⁸, a 7% mass concentration PVA aqueous solution was made. The solution was poured into a 3D printed mould designed in Rhino3D⁹ (Figure 1), and subsequently underwent 3 freeze-thaw cycles. 15% mass concentration PVA solution was used to create stiffer inclusions in the heterogeneous phantom, emulating fibrotic or scarred regions. Inclusions were mixed with gadolinium contrast agent to facilitate their localisation in the MRI images.

An intraventricular balloon filled with water was used to inflate the cavity to the end-diastolic volume, over three volume increments (Figure 1). The experimental setup was placed in a 3T Philips Achieva scanner. The waves were generated by an electromagnetic transducer, at a driving frequency of 150 Hz. At each deformation state, high resolution T2-weighted anatomical images as well as MRE data were acquired¹⁰ (Figure 2).

The wave images were used for reconstructing the phantoms' mechanical properties. The technique applied was based on a local divergence free finite element reconstruction integrated with nonlinear perturbation theory to account for theoretical amplification due to deformation state. The technique was applied on all deformation states, with either the corrected reconstruction (CR) accounting for deformations, or, uncorrected reconstruction (UR) effectively neglecting deformations. Deformation fields were approximated using finite element models (Figure 3). Meshes corresponding to the reference phantom geometries were inflated to various loading states¹¹. Restrictions in motion imposed by the supporting boards and the transducer were accounted through appropriate boundary conditions¹¹. The PVA material behaviour was approximated by the neo-Hookean law, and increased values were assigned on the stiffer inclusions.

Results and Discussion

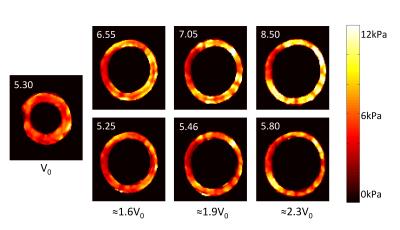
The mechanical properties of the homogeneous phantom were reconstructed at each deformation state, using UR and CR. Figure 4 presents the average elasticity (real part G' of complex shear modulus G*=G'+iG''). The apparent stiffness with UR was up to 60% higher than the reference value. However, with CR, the reference elasticity was retrieved in all states with a maximum error < 10%.

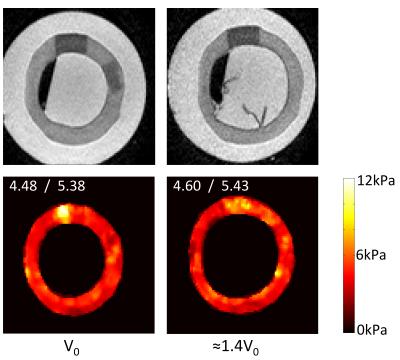
CR was also applied on the heterogeneous phantom (Figure 5). The maximum G' regions coincide with the stiffer inclusions, demonstrating the ability of CR to identify stiffer – and thus potentially diseased – regions. Furthermore, CR was able to retrieve the reference elasticity for both the normal and stiffer regions.

Conclusions

Acknowledgements

References

1. Wang J, Nagueh S. Current perspectives on cardiac function in patients with diastolic heart failure. Circulation. 2009;119:1146–1157.

2. Bortone A, Hess O, Chiddo A, et al. Functional and structural abnormalities in patients with dilated cardiomyopathy. J. Am. Coll. Cardiol. 1989:14:613–623.

3. Hadjicharalambous M, Asner L, Chabiniok R, et al. Non-invasive model-based assessment of passive left-ventricular myocardial stiffness in healthy subjects and in patients with non-ischemic dilated cardiomyopathy. Ann. Biomed. Eng. 2016.

4. Sinkus R, Siegmann K, Xydeas T, et al. MR Elastography of Breast Lesions: Understanding the Solid/Liquid Duality Can Improve the Specificity of Contrast-Enhanced MR Mammography. Magn. Reson. Med. 2007; 58(6):1135-1144.

5. Huwart L, Sempoux C, Vicaut E, et al. Magnetic Resonance Elastography for the Noninvasive Staging of Liver Fibrosis. Gastroenterology. 2008; 135(1):32-40.

6. Clarke E, Cheng S, Green M, et al. Using static preload with magnetic resonance elastography to estimate large strain viscoelastic properties of bovine liver. J. Biomech. 2011; 44(13), 2461-2465.

7. Fovargue D, Sinkus R, Nordsletten D. Robust MR elastography stiffness quantification using a localized divergence free finite element reconstruction. ISMRM. 2017.

8. Surry K, Austin H, Fenster A, Peters T. Poly(vinyl alcohol) cryogel phantoms for use in ultrasound and MR imaging. Phys.Med. Biol. 2004;49:5529–5546.

9. http://www.rhino3d.co.uk/

10. Garteiser P, Sahebjavaher R, Ter Beek, et al. Rapid acquisition of multifrequency, multislice and multidirectional MR elastography data with a fractionally encoded gradient echo sequence. NMR in biomedicine. 2013;26:1326-1335.

11. Asner L, Hadjicharalambous M, Chabiniok R, et al. Patient-specific modeling for left ventricular mechanics using data-driven boundary energies.CMAME. 2016;1-27.