2676
Unilateral Linear Halbach magnets for single sided magnetic resonance: generalized design framework and experimental validation1Electrical Engineering & Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 2David H. Koch Institute For Integrative Cancer Research, Massachusetts Institute of Technology, Cambridge, MA, United States, 3Harvard–MIT Program of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, United States, 4Department of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA, United States
Synopsis
Single-sided NMR has the potential for broad utility, especially as a portable diagnostic for disorders in fluid regulation. These sensors require a remote, high field, uniform magnetic field to achieve sufficient sensitivity. We demonstrate a new magnet geometry, the Unilateral Linear Halbach, that combines design principles from sweet-spot and linear Halbach magnets to achieve this goal. Sensitivity analysis using finite element analysis produces a generalized framework for Unilateral Linear Halbach design. Experimental validation through the fabrication of a magnet assembly shows close agreement with the simulated magnetic field. Unilateral Linear Halbach magnets increase the sensitivity, portability, and versatility of single sided NMR.
Background and Purpose
Unilateral, or single-sided, nuclear magnetic resonance (NMR) sensors are applicable to many biomedical applications, especially portable diagnostics for fluid regulation disorders due to the inherent sensitivity of NMR to changes in water distribution1,2. Measurement of the fluid distribution in lean muscle tissue offers potential in managing fluid disorders such as dehydration and volume overload3. However, accessing this tissue for measurement requires that the measurement penetrate beneath the subcutaneous tissue4. The ability of single-sided NMR systems to interrogate tissue remote to the surface of the sensor enables measurements of anatomical regions previously not possible with closed bore systems5.
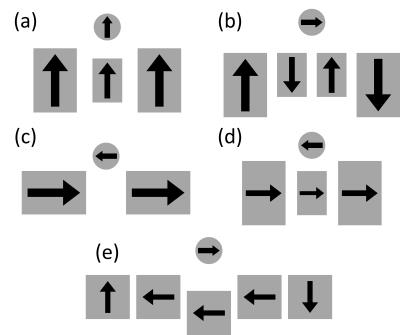
Single-sided NMR relies on a remote, large, high field strength uniform magnetic field oriented parallel to the surface of the magnet to maintain high sensitivity measurements with standard surface coils6,7. A large uniform region has been demonstrated by previous designs (Figure 1a-d), but these suffer from low field strength due to inefficient utilization of available magnetic flux8,9. Linear Halbach array magnets concentrate the magnetic flux to one side of the magnet, but are unsuitable for remote measurement due to the high field gradient produced at the surface10.
We demonstrate a new magnet geometry, the Unilateral Linear Halbach (Figure 1e), that achieves high field strength over a large homogeneous region by combining design principles from sweet-spot and linear Halbach magnets.
Methods
Definition of magnet geometry
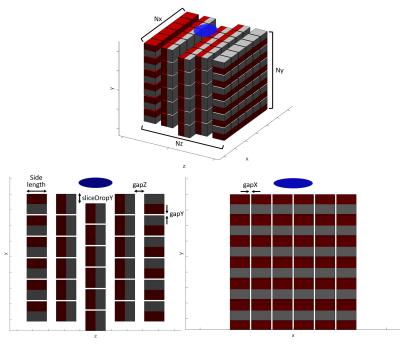
The magnet consists of hundreds of identical neodymium cube magnets whose relative position defines a magnet assembly. The number of slices, the number of magnets, the relative position and orientation of the slices, and the gaps between the magnets collectively describe the magnet assembly (Figure 2).
Performance criteria for evaluation of magnetic field
Finite element analysis using COMSOL Multiphysics (Burlington, MA) was performed to simulate the remote magnetic field generated by the magnet design.
Metrics were derived from the magnetic field which defined its geometry and strength to compare the fields generated by magnets with different configurations. The uniform region was found by finding the contiguous region, $$$B_z(x,y,z)$$$ defined over the volume $$$V$$$, which maximized an approximation of the signal to noise ratio (SNR) of a thermal noise limited NMR experiment7:
$$SNR\cong\int_{V}B_z(x,y,z)^{7/4}dV$$
The maximum field deviation within the uniform region, $$$B_z(V)$$$, was constrained to less than, $$$\epsilon$$$ (1%), which represents a reasonable bandwidth for the RF excitation pulse13:
$$\frac{max(B_z(V))-min(B_z(V))}{B_{z,0}}\leq\epsilon$$
The maximum angular deviation of the magnetic field was constrained as off-axis precession can introduce artifacts into the measurement
$$\arctan\sqrt{\frac{B_x(V)^2 + B_y(V)^2}{B_z(V)^2}}\leq1\%\space\forall \space V$$
The following metrics were computed to allow comparisons between magnet designs: field strength, size of uniform region, and its depth from the surface of the magnet. These metrics are used to design the optimal magnet based on the desired application.
Results
Simulations of magnet performance produce a generalized influence matrix
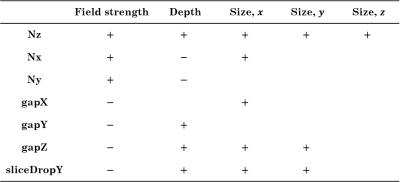
Simulations of the performance of the magnet assembly as parameters were varied, individually and in conjunction with each other, yielded an influence matrix (Table 1). This analysis shows how each metric used to characterize the magnetic field varies in response to each of the design parameters. This provides a generalizable understanding to guide future single-sided magnet assemblies based on the Unilateral Linear Halbach design.
Experimental demonstration validates simulations and design methods
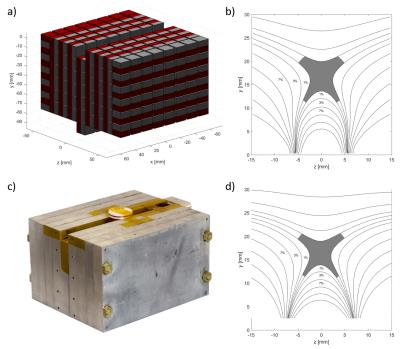
The volume of the uniform region (>1000 mm3), field strength (>0.2 Tesla), measurement depth (>15 mm), and magnet volume (<1000 cm3) were fixed based on design requirements set forth by our application (portable single sided NMR relaxometry of lean muscle tissue to measure hydration).
The uniform region (258 mTesla) produced by the magnet (Figure 3) was located 17 mm from the surface of the magnet and was 3 mm wide (x-axis), 5 mm tall (y-axis), and 18 mm long (z-axis) for a total volume of 1300 mm3. The shape of the field from the constructed magnet agreed with numerical models, however its strength was approximately 30% lower. We are currently unable to explain this discrepancy though it is likely due to magnet and assembly non-idealities.
Discussion and Conclusion
The Unilateral Linear Halbach magnet offers remote, high field, low gradient homogeneous regions for clinical single sided NMR. Our experimental demonstration closely matches numerical models indicating the effectiveness and simplicity of both our approach and this design. While the design utilized an array of identical magnets, rather than a few larger magnets to allow for increased design flexibility, ultimately this magnet could be constructed with far fewer magnets to simplify construction. The influence matrix produced from simulations builds a generalized framework for future magnet designs. Initial studies have demonstrated the utility of these magnets in single-sided NMR systems for diagnostic applications.Acknowledgements
Funding from MIT Institute for Soldier Nanotechnologies (United States Army Research Office Grant W911NF-13D-0001), National Institutes of Health – National Cancer Institute Centers of Cancer Nanotechnology Excellence Grant U54 CA151884-02, a Hertz Foundation Graduate Fellowship, and a National Science Foundation Graduate Fellowship.References
1. Tavassolian, N., Li, M., Vassiliou, C. C. & Cima, M. J. A novel magnetic relaxation-based platform for hydration monitoring. IEEE Sens. J. 14, 2851–2855 (2014).2. Li, M., Vassiliou, C. C., Colucci, L. a & Cima, M. J. (1)H nuclear magnetic resonance (NMR) as a tool to measure dehydration in mice. NMR Biomed. 28, 1031–9 (2015).
3. Hackney, K. J., Cook, S. B., Fairchild, T. J. & Ploutz-Snyder, L. L. Skeletal muscle volume following dehydration induced by exercise in heat. Extrem. Physiol. Med. 1, 3 (2012).
4. SONG, T. Subcutaneous tissue depth differences between males and females*1The need for gender based epinephrine needle. J. Allergy Clin. Immunol. 113, S241 (2004).
5. Casanova, F., Perlo, J. & Blümich, B. Single-sided NMR. Single-Sided NMR (Springer Berlin Heidelberg, 2011). doi:10.1007/978-3-642-16307-4
6. Casanova, F. & Blümich, B. Two-dimensional imaging with a single-sided NMR probe. J. Magn. Reson. 163, 38–45 (2003).
7. Hoult, D. I. & Richards, R. E. The signal-to-noise ratio of the nuclear magnetic resonance experiment. J. Magn. Reson. 24, 71–85 (1976).
8. Marble, A. E. Strong, stray static magnetic fields. IEEE Trans. Magn. 44, 576–580 (2008).
9. Marble, A. E., Mastikhin, I. V., Colpitts, B. G. & Balcom, B. J. A compact permanent magnet array with a remote homogeneous field. J. Magn. Reson. 186, 100–104 (2007).
10. Chang, W. H., Chen, J. H. & Hwang, L. P. Single-sided mobile NMR with a Halbach magnet. Magn. Reson. Imaging 24, 1095–1102 (2006).
11. Blümich, B. et al. Simple NMR-MOUSE with a bar magnet. Concepts Magn. Reson. Part B Magn. Reson. Eng. 15, 255–261 (2002).
12. García-Naranjo, J. C., Mastikhin, I. V, Colpitts, B. G. & Balcom, B. J. A unilateral magnet with an extended constant magnetic field gradient. J. Magn. Reson. 207, 337–344 (2010).
13. Kobzar, K., Skinner, T. E., Khaneja, N., Glaser, S. J. & Luy, B. Exploring the limits of broadband excitation and inversion pulses. J. Magn. Reson. 170, 236–243 (2004).
Figures