2644
Numerical Simulation of Specific Absorption Rate (SAR) Induced in the Head as a Function of EEG Lead Conductivity during 256-channel dEEG/fMRI at 3T.1Harvard Medical School, Boston, MA, United States, 2Massachusetts General Hospital, Boston, MA, United States, 3Mechanical Engineering, University of Maryland, MD, United States, 4Electrical Geodesics Inc., OR, United States
Synopsis
This study presents the numerical quantification of the relationship between the EEG lead conductivity and SAR induced in the head in EEG-fMRI at 3T and using a 256-channel dense array sensor net. SAR induced in the head normalized by the gold standard of no sensor net was an S-curve function of the EEG lead conductivity in the range 1S/m - 5.8.107 S/m, plateauing at 1 for lead conductivities below 10 S/m.
Background
EEG-fMRI with high spatial and temporal resolution is a useful technique for studying brain function [1, 2]. However, the Radio Frequency (RF) field of MRI can induce current in the conductive EEG leads resulting in increased Specific Absorption Rate (SAR) in the head [3, 4]. Prior research has shown that SAR induced in the head is directly related to lead conductivity and also varies with number of leads, RF frequency and coil model [5-9]. Previous numerical studies using Finite-Difference Time-Domain (FDTD) simulations have estimated the relationship between EEG lead conductivity and SAR induced in the head [7, 8]. However, these numerical studies were limited to only a few lead conductivity values that do not allow a comprehensive analysis of the relationship between EEG lead conductivity and SAR induced in the head. Furthermore, FDTD numerical studies are affected by staircasing issues when modeling the small and curved structures of the EEG electrodes/leads [7, 8, 10, 11], resulting in inaccuracies in the estimation of local SAR peaks. This study used Finite Element Method (FEM) to more precisely analyze the relationship between EEG lead conductivity and SAR induced in an anatomically accurate head model wearing a 256-channel dense array (dEEG) sensor net and placed in a tuned 3 Tesla MRI coil.Methods
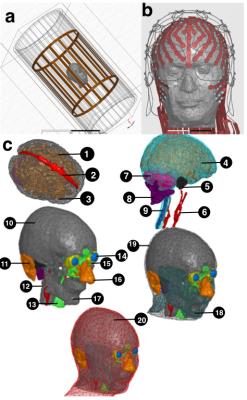
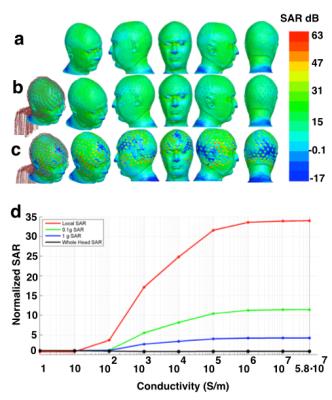
An anatomically accurate head model [12], realistic MRI transmit [13] and receive coils and a 256-channel dEEG sensor net (700mm long, 8 mm wide sheet traces) models were used for numerical SAR analysis (Fig. 1). Tissue dielectric constants were assigned according to the Larmor frequency of a 3T scanner (e.g. 128 MHz) [14]. High Frequency Structural Simulator (HFSS) solver (ANSYS, Burlington, MA) was then used to estimate SAR in the head having no sensor net (No-Net). Simulations were run at the Larmor frequency of a 3T scanner (e.g. 128 MHz) and on a PC with two Intel (Santa Clara, CA) E5-2695V3 CPUs each with 14 cores and 512 GB of RAM. Following simulation convergence, the MRI transmit coil was tuned according to the procedures explained in [13] ensuring that SAR averaged in the whole head without any net (No-Net) is 3.2 W/kg [13]. Once the MR-transmit coil was tuned, SAR was also estimated for the head model with dEEG net and for nine lead conductivities in the range 1 S/m to 5.8.107 S/m (copper). Peak of point-SAR (1 mm3 resolution), peak of SAR averaged in 0.1 g and 1 g tissue, and SAR averaged in the whole head were then estimated for each of the nine EEG lead conductivities and normalized by the gold standard of No-Net.Results
Our results indicated that SAR averaged in the whole head normalized by the gold standard of No-Net is around 1 for all nine lead conductivities. However, peak of point-SAR and peak of SAR averaged in 0.1 g and 1 g head tissue showed SAR hot spots for the high-conductive EEG leads of 5.8.10 S/m (Fig. 2). It was observed that SAR decreased as an S-curve function of EEG lead conductivity, and that point-SAR normalized by the gold standard of No-Net did not reach a plateau minimum until conductivity decreased to 10 S/m (Fig. 2).Conclusions
Our results taking advantage of realistic FEM modeling allowed precise quantification of the relationship between SAR induced in the head and EEG lead conductivity across a wide range of lead conductivities. With the lead geometries modeled here, these results suggest that lead conductivities of 10 S/m or less are required for no SAR change in the head with respect to the gold standard of No-Net. It should also be noted that direct temperature safety conclusions cannot be made from these SAR results and further temperature simulations are required for such purposes.Acknowledgements
NIH grant R44NS071988References
1. Herrmann C. S. and Debener S. Simultaneous recording of EEG and BOLD responses: a historical perspective. International Journal of Psychophysiology, 2008;(67): 161-168.
2. Mullinger K. and Bowtell R., "Combining EEG and fMRI," in Magnetic Resonance Neuroimaging: Methods and Protocols, M. Modo and W. M. J. Bulte, Eds., ed Totowa, NJ: Humana Press, 2011, pp. 303-326.
3. Serano P., Angelone L. M., Katnani H., et al. A novel brain stimulation technology provides compatibility with MRI. Scientific reports, 2015;(5)
4. Guy A. Biophysics-energy absorption and distribution. AGARD Lecture Series, Radiation Hazards (Non-ionizing Radiations – Biological Effects and Safety Considerations 78. 1975;
5. Collins C. M., Liu W., Wang J., et al. Temperature and SAR calculations for a human head within volume and surface coils at 64 and 300 MHz. Journal of Magnetic Resonance Imaging, 2004;(19): 650-656.
6. Scarff C. J., Reynolds A., Goodyear B. G., et al. Simultaneous 3-T fMRI and high-density recording of human auditory evoked potentials. Neuroimage, 2004;(23): 1129-1142.
7. Angelone L. M., Potthast A., Segonne F., et al. Metallic electrodes and leads in simultaneous EEG-MRI: Specific absorption rate (SAR) simulation studies. Bioelectromagnetics, 2004;(25): 285-295.
8. Angelone L. M., Vasios C. E., Wiggins G., et al. On the effect of resistive EEG electrodes and leads during 7 T MRI: simulation and temperature measurement studies. Magnetic resonance imaging, 2006;(24): 801-812.
9. Poulsen C., Wakeman D. G., Atefi S. R., et al. Polymer thick film technology for improved simultaneous dEEG/MRI recording: Safety and MRI data quality. Magnetic resonance in medicine, 2016;
10. Holland R. Pitfalls of staircase meshing. IEEE Transactions on Electromagnetic Compatibility, 1993;(35): 434-439.
11. Railton C. J. and Schneider J. B. An analytical and numerical analysis of several locally conformal FDTD schemes. IEEE Transactions on Microwave Theory and Techniques, 1999;(47): 56-66.
12. Makris N., Angelone L., Tulloch S., et al. MRI-based anatomical model of the human head for specific absorption rate mapping. Medical & biological engineering & computing, 2008;(46): 1239-1251.
13. Bonmassar G., Serano P., and Angelone L. M., "Specific absorption rate in a standard phantom containing a Deep Brain Stimulation lead at 3 Tesla MRI," in Neural Engineering (NER), 2013 6th International IEEE/EMBS Conference on, 2013, pp. 747-750.
14. Gabriel C. G. a. S. Compilation of the dielectric properties of bodytissues at RF and microwave frequencies. Available: http://niremf.ifac.cnr.it/docs/DIELECTRIC/Report.html. (1996);
Figures