Introduction

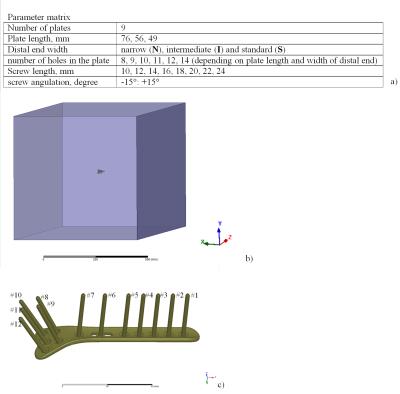
Most of commercially available implants are multi-component devices. With FDA released guidance FDA-2015-D-2104¹, reliability requirements for RF-induced assessment significantly increased compared to standard ASTM F2182-11a² used widely in the past. Our goals were to analyze 64 and 127.7 MHz RF-induced heating of a distal radius implant system by: 1) simulating relevant configurations of one plate with longest length and narrow width of distal end to reveal different hotspot locations; 2) simulating other 8 plates with the screw configurations derived from analysis done for the first plate.

Method

A system parameter matrix is shown in Fig. 1a. The plate and screws were placed in the middle of a box with dimensions 600x600x2400 mm³, filled with a medium with relative electric permittivity of 78 and electrical conductivity of 0.65 S/m, representing human muscle. The box was excited from one side by a 64 or 127.7 MHz source (Fig.1b). The screws were simulated as “nails” (Fig 1.c) to reduce computational complexity while only slightly increasing the temperature results uncertainty (~15%)³. A 3-D temperature distribution after 15 minutes continuous excitation with tangential electric field E_tan(z)=100 V/m (peak-to-peak) was obtained by 3-D EM and thermal co-simulations. The maximum temperature rise (ΔT_max) was calculated as the highest difference of spatial temperature distribution for cases with and without the implant. For the first plate (N76) random trials followed by a gradient based investigation included 30 co-simulations at both 64 and 127.7 MHz. The remaining eight plates were simulated in only five configurations. Three configurations were derived from the gradient analysis of the first plate. To obtain a base line level estimation all plates were also simulated in two configurations: all screws with 24 mm length (AS24), and all screws with 10 mm length (AS10).

Results and discussion

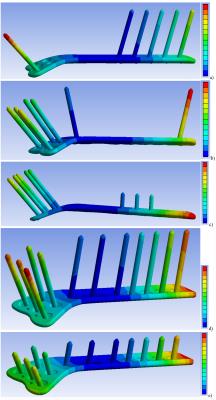
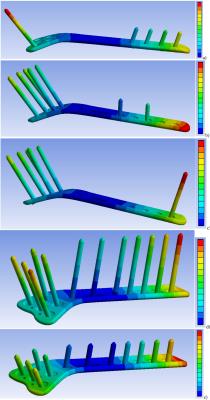
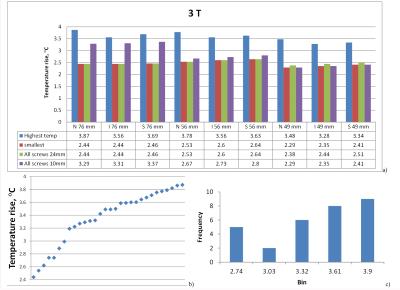
30 simulations were less than required to cover an entire parameter matrix using Monte-Carlo analysis with reasonable uncertainty. However at both 64 and 127.7 MHz, three screw configurations resulting in high ΔT_max (Fig. 2a-c and Fig. 3a-c) were revealed. The locations of ΔT_max were observed in the medium in close proximity of: screw #1 with -15° angle, screw #12 with 15° angle, and plate end face, respectively. ΔT_max variation for these cases was less than 12% and was ~75% higher than the minimum ΔT_max obtained (Fig. 4). Neighboring configurations suggested by gradient analysis, for example use of screws #10 or #11 instead of screw #12, resulted in a slightly decreased ΔT_max. For N76 , configurations AS24 and AS10 resulted in relatively moderate ΔT_max. At 64 MHz one of randomly selected configurations resulted in 20% smaller ΔT_max than for AS24 and AS10. At 127.7 MHz configuration AS24 resulted in the smallest ΔT_max (Fig.5). For all plates and frequencies investigated: a) AS24 and AS10 configurations did not result in the highest ΔT_max; b) ΔT_max for AS24 was not always higher that ΔT_max for AS10. Because gradient analysis was done only for N76, there is no guaranty that for other plates the highest ΔT_max was calculated. However because a) all plates were electrically short, b) the longest plate was investigated by gradient analysis, and c) the gradient analysis showed smooth behavior of ΔT_max across configurations that resulted in highest ΔT_max, a scientific rationale could be that for other plates, the difference between the highest ΔT_max and the smallest ΔT_max for AS24 and AS10 should be similar to this difference for N76. Thus based on available results the highest ΔT_max across all plates was estimated as (3.44+1.55)=4.99°C for 64 MHz and (2.64+1.43)=4.07°C for 127.7 MHz, which is a bit higher than the corresponding maximum ΔT_max obtained across all simulations. Cumulative numerical uncertainty for the given numerical setup was estimated as less than 10%. However single surrounding tissue approximation and only one orientation of the plate relative to the incident field propagation were substantial simplifications of different in-vivo multi-tissue cases. No uncertainties for these simplifications of very complex real cases, and possible variation of thermal and electrical properties were estimated in the given study.

Conclusion

Because of the smooth outcome of random trials followed by a gradient analysis, even relatively small simulation numbers allowed to reveal the configuration with the highest ΔT_max for a given E_tan(z). Our case study provided strong evidence that 3T static field strength cannot be considered as a worst-case for RF-induced heating. The specific results of this study, e.g., dependence of ΔT_max on plate dimension and screw configuration, cannot be simply extrapolated to other implants. This investigation without additional physical tests in MR environment is not sufficient to claim MR Conditional according to ASTM F2503.

Acknowledgements

No acknowledgement found.