2608
Abdominal organ tracking on a hybrid MR-Linac system using a particle filter based algorithm1Département de radio-oncologie, Centre Hospitalier de l'Université de Montréal, Montréal, QC, Canada, 2Département de physique, Université de Montréal, Montréal, QC, Canada, 3Imaging division, UMC Utrecht, Utrecht, Netherlands, 4Radiation Oncology, Medical College of Wisconsion, Milwaukee, WI, United States, 5Radiology, Medical College of Wisconsin, Milwaukee, WI, United States
Synopsis
We have previously developed an autocontouring and tracking algorithm for lung tumors as an online application for MR-Linac treatments. This algorithm is now extended to abdominal organs tracking and evaluated with a range of imaging strategies on multiple systems, including single slice dynamic time-series data acquired on the 1.5T Marlin system of the MR-Linac as well as simultaneous multi-slice (SMS) and simultaneous orthogonal plane imaging (SOPI) acquired on diagnostic 1.5T Philips and 3T Siemens scanners. The wide adaptability of the algorithm on images of different contrast concludes that the method is robust and can be successfully applied in different tracking scenario.
Purpose/objective
We have previously developed a particle filter based tracking and autocontouring algorithm for lung tumors as a real-time tracking application for MR-Linac (MRL) treatments, allowing tracking of the tumor in 6 ms.1 In this work, we present a modification of the method to enable tracking in the abdomen. The robustness of the technique is demonstrated by tracking several regions of interest with a range of imaging strategies on multiple systems, including single slice dynamic time-series data acquired on the 1.5T Marlin system of the MR-Linac as well as simultaneous multi-slice (SMS) and simultaneous orthogonal plane imaging (SOPI)2 acquired on diagnostic 1.5T Philips and 3T Siemens scanners.Material/methods
A sequential Monte Carlo method called particle filter is used to track abdominal regions of interest of healthy volunteers.3 The filtering equation is based on the states, $$$\mathrm{X}_t=\{{\bf x}_1, ..., {\bf x}_{t-1},{\bf x}_t\}$$$, and the observations, $$$\mathrm{Z}_t=\{{\bf z}_1,...,{\bf z}_{t-1},{\bf z}_t\}$$$, from time 1 to $$$t$$$:
$$\mathrm{{Pr}}({\bf x}_t|\mathrm{Z}_t)\propto\mathrm{{Pr}}({\bf z}_t|{\bf x}_t)\int\mathrm{{Pr}}({\bf x}_t|{\bf x}_{t-1})\mathrm{{Pr}}({\bf x}_{t-1}|\mathrm{Z}_{t-1})\mathrm{d}{\bf x}_{t-1}$$ ,
where $$$\mathrm{{Pr}}({\bf x}_t|\mathrm{Z}_t)$$$ is the probability of $$${\bf x}_t$$$ given $$$\mathrm{Z}_t$$$ , called the posterior estimate. $$$\mathrm{{Pr}}({\bf z}_t|{\bf x}_t)$$$ is the observation model or likelihood, $$$\mathrm{{Pr}}({\bf x}_t|{\bf x}_{t-1})$$$ is the dynamic model and $$$\mathrm{{Pr}}({\bf x}_{t-1}|\mathrm{Z}_{t-1})$$$ is the posterior estimate at time $$$t-1$$$. The algorithm is adapted to abdominal anatomies by calculating the likelihood of the particles based on normalized cross-correlation:
$$\mathrm{{Pr}}({\bf z}_t|{\bf x}_t^{i}) = \frac{1}{\sigma\sqrt{2 \pi}}e^{-\frac{(\mathrm{NCC}_t^{i})^2}{2\sigma^2}}$$ .
The preliminary steps of the algorithm only include the definition of an ROI encompassing the organ’s movement during the respiratory cycle and the delineation of the organ of interest on ten images in order to create the template used for the normalized cross-correlation.
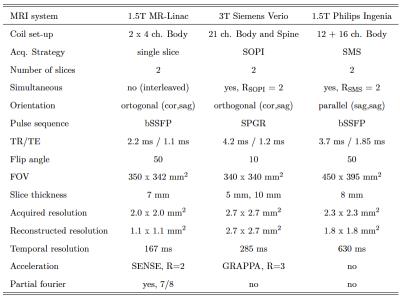
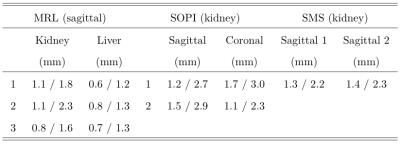
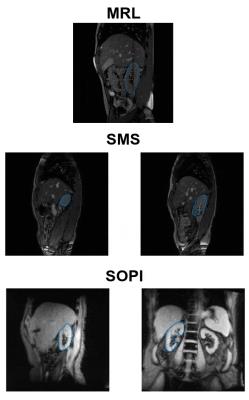
Experiments. To test the robustness of the algorithm, data were acquired using product cine MRI pulse sequence available on the MR-Linac as well as two recently developed simultaneous multi-slice approaches. The SMS and SOPI pulse sequences are currently only implemented on diagnostic scanners, but will be transferred to the MR-Linac as soon as its full installation is completed. A total of five healthy volunteers were scanned on three different systems: 1) three volunteers were scanned on the 1.5T Philips Marlin scanner of the MR-Linac using an interleaved orthogonal bSSFP acquisition, 2) 2-fold accelerated SMS-CAIPIRINHA bSSFP data were obtained in one volunteer on a 1.5T Philips Ingenia (Philips, Best), and 3) two SOPI data sets were obtained in one volunteer on a 3T Siemens Verio (Siemens, Erlangen). Scanner parameters are provided in Table 1. As shown in Figure 1, the algorithm is evaluated for the three imaging strategies: for the MR-Linac data, only the sagittal plane is used in order to be able to track both a landmark in the liver and the kidney. Second, the algorithm is applied on multi-band acquisitions of two simultaneous sagittal planes passing through the kidney. Lastly, SOPI images data sets of two different slice thicknesses, 5 mm and 10 mm, are used as a final comparison. To evaluate the accuracy, the mean errors are computed between the centroid of the region of interest estimated by the algorithm and the ground truth, which is defined as the centroid obtained by manually propagating a contour over the full length of the acquisition.
Results/discussion
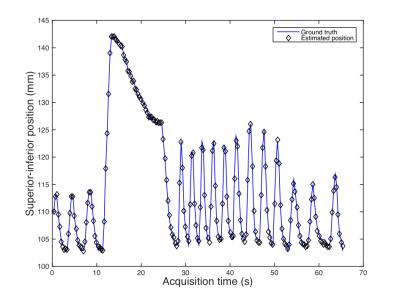
The mean error and 95th percentile are presented in Table 2 for all regions of interest and imaging strategies. In summary, the tracking errors were found to be smaller than the image resolution in each case evaluated. Since the images acquired on the MRL system have the highest resolution, the mean tracking errors on the kidney are the lowest for this modality. As shown in Figure 2, the results are independent of the position in the respiratory cycle and of the amplitude of motion. Likewise, the tracking accuracy isn’t affected by the breathing challenges instructed to the volunteers. Further, our tracking algorithm appears unaffected by the saturation line produced by the orthogonal plane as seen in the MRL and the SOPI images (Figure 3). Since the computational time of the algorithm is dependent on the number of particles and the area of the ROI, future work will focus on timing optimization.Conclusion
This proof of concept shows the automated tracking feasibility of various organs on dynamic images from different sequence acquisitions and imaging strategies that could potentially be implemented for MRL online adaptive treatments. The wide adaptability of the algorithm on images of different contrast concludes that the method is robust and can be successfully applied in different tracking scenario. In conclusion, this particle filter based tracking algorithm offers a promising and adaptable method for online tracking MRL treatments.Acknowledgements
AEB is supported by the Natural Sciences and Engineering Research Council of Canada.References
1. A.E. Bourque, S. Bedwani, E. Filion, J.-F. Carrier, “A particle filter based autocontouring algorithm for lung tumor tracking using dynamic magnetic resonance imaging,” Medical Physics 43, 5161 (2016).
2. N.J. Mickevicius and E.S. Paulson, “Simultaneous Orthogonal Plane Imaging,” Magn. Reson. Med. (Accepted, 2016).
3. M.S. Arulampalam, S. Maskell, N. Gordon, and T. Clapp, "A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking," IEEE Trans. Signal Process. 50, 174-188 (2002).
Figures