2591

Fast Temperature Estimation Using Golden Angle Radial from Undersampled K-Space for MR Guided Microwave Ablation
Ke Wang1, Zijing Dong2, Fuyixue Wang2, Bingyao Chen3, Jiafei Yang3, Xing Wei3, and Kui Ying4

1Department of Biomedical Engineering, Tsinghua University, Beijing, People's Republic of China, 2Center for Biomedical Imaging Research, Department of Biomedical Engineering, Tsinghua University, Beijing, People's Republic of China, 3Department of Orthopedics, First Affiliated Hospital of PLA General Hospital, Beijing, People's Republic of China, 4Key Laboratory of Particle and Radiation Imaging, Ministry of Education, Medical Physics and Engineering Institute, Department of Engineering Physics, Tsinghua University, Beijing, People's Republic of China

Synopsis

Golden angle radial sampling is insensitive to motion and provides oversampled central k-space for self-navigation. This study aims to accelerate the acquisition with motion correction for MR temperature imaging by applying golden angle radial to hybrid model based on PRF method. The proposed method uses low resolution images obtained from a certain ratio of radius in k-space center to correct the period motion and magnetic field drift. Then, an iterative method is adopted to estimate the temperature by the hybrid model. Simulations and in-vivo experiments demonstrate the robustness to motion and effectiveness of the proposed method.

Purpose

In microwave ablation, it is important to achieve accurate real time temperature monitoring during the operation. Considering the fact that PRF-based temperature mapping is very sensitive to motion, the conventional k-space-based hybrid[1] approach can improve the accuracy of temperature through combination of hybrid multi-baseline[2] and referenceless[3] method for motion correction. However, the large loop iterations of the conventional approach could be relatively time-consuming in computation. To reduce the computation time, our group proposed a fast k-space temperature estimation method using Cartesian sampling with oversampled k-space center as navigator for motion correction[4]. Golden angle (GA) radial sequence is insensitive to motion and provides oversampled k-space center as a self-navigator, which should be a better candidate for k-space hybrid reconstruction. Therefore, the present study proposes a reconstruction method based on golden angle radial (GA) sampling to achieve temperature mapping acceleration while maintaining accuracy in the presence of motion.

Methods

The proposed method estimates temperature changes from undersampled GA radial data based on the hybrid model[1]，which could be expressed as:$$y_{i}=\sum_{j=1}^{N_{s}}e^{i\overrightarrow{k_{i}}\cdot\overrightarrow{x_{j}}}\left(\sum_{l=1}^{N_{b}}b_{l,j}{w_{l}}\right)e^{i({\left\{Ac\right\}}_j+\theta_{j})}+\epsilon_{i}$$ where $$$y_{i}$$$ is one k-space data sample, $$$N_{s}$$$ is the number of image voxels, $$$\overrightarrow{k_{i}}$$$ is the k-space location of sample $$$i$$$, $$$\left\{b_{l}\right\}_{l=1}^{Nb}$$$ are complex baseline library images which acquired before heating with different motion states, $$$w_{i}$$$ are baseline image weights, $$$A$$$is a matrix of smooth basis function, $$$c$$$ is a polynomial phase coefficient vector, $$$\theta$$$ is a heating-induced phase shift and $$$\epsilon$$$ is complex Gaussian noise[1].

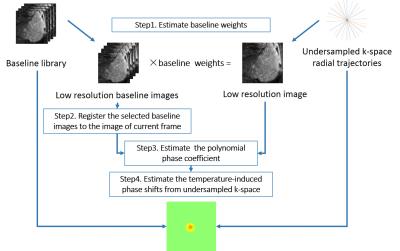
As shown in Fig.1, the first step of the proposed method is the estimation of the baseline library weights to correct the period motion[1]. In this study the weights of multi-baseline images are calculated by utilizing information from low resolution images[4] reconstructed by the data with a certain ratio of radius in k-space center. The second step is using the unheated region of the low resolution images to calculate the polynomial phase coefficients for correcting the magnetic field drift[4]. Finally, the temperature estimation is conducted using an iterative method with smooth constraint.

Experimental Designs

The phantom and, in-vivo experiments with heating simulation were performed to investigate the efficiency of the proposed method. The phantom and in-vivo (liver, spine) data with large motion errors due to dynamic acquisition were acquired on a Philips 3T system (Philips Healthcare, Best, the Netherland) respectively.

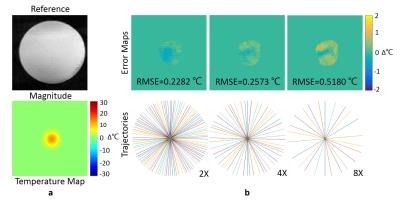
An agar phantom without heating was acquired using GA radial sequence for testing the accuracy and the computation time of the proposed algorithm. Then a Gaussian phase was added manually on the images to simulate heating (+25℃). The imaging parameters were: FOV = 160×160 mm2, in-plane resolution = 2×2 mm2, TR/TE = 50/10 ms, flip angle = 15°.

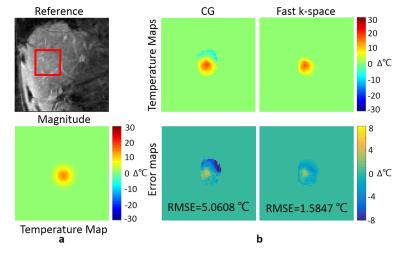
The in-vivo liver experiment with simulated heating was conducted to measure the robustness to motion and the temperature accuracy. The data was acquired using a Cartesian sequence and then converted into GA radial data using NUFFT. The scan parameters were: FOV = 240×307.5 mm2, in-plane resolution = 2×2 mm2, TR/TE = 50/10 ms, flip angle = 15°.

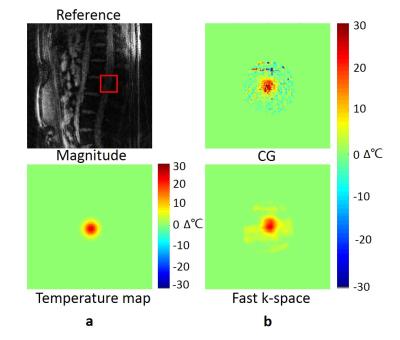
The in-vivo spine experiment without heating was performed to evaluate the performance of the proposed method for regions with complicated structures. The image was acquired using GA radial sequence on a health volunteer with following scan parameters: FOV = 256×256 mm2, in-plane resolution = 2×2 mm2, TR/TE = 30/10 ms, flip angle = 15°.

In addition, full-sampled CG temperature reconstructions were also implemented for comparison using the same sampling pattern in each experiment.

Results

In phantom heating simulations, the proposed method gave a relatively lower RMSEs and less computation time: the RMSE of the image at 4x acceleration is 0.2573℃ with computation time 6.63s, which was much shorter than the conventional hybrid model[4] (Fig.2).

In the liver experiment, the RMSE of the full-sampled CG reconstruction without motion correction is 5.0608℃ while the RMSE of the GA fast k-space reconstruction at 4x acceleration is 1.5847℃ (Fig.3).

The second in-vivo experiment was the GA sampling spine temperature reconstruction with lower SNR. When applying the radial sampling fast k-space methods under the acceleration factor of 4, the error of the temperature was much lower than the full-sampled CG reconstruction due to the motion correction and smooth constraint (Fig.4).

Discussion and Conclusion

According to the results, both phantom and in-vivo experiments validated the effectiveness of the proposed fast k-space estimation using GA radial for more accurate temperature estimation with corrected motion-induced errors. In addition, the accelerated acquisition by undersampling and relative short computation time of the proposed method make real-time temperature monitoring for MR-guided microwave ablation feasible.

Acknowledgements

This work is supported by Students Research Training (SRT) research funding from Tsinghua University.

References

[1] Gaur P, Grissom W A. Accelerated MRI thermometry by direct estimation of temperature from undersampled k-space data.[J]. Magnetic Resonance in Medicine, 2015, 73(5):1914–1925.

[2] Vigen K K, Daniel B L, Pauly J M, et al. Triggered, navigated, multi-baseline method for proton resonance frequency temperature mapping with respiratory motion.[J]. Magnetic Resonance in Medicine, 2003, 50(5):1003-10.

[3] Grissom W, Pauly K B, Lustig M, et al. Regularized referenceless temperature estimation in PRF-shift MR thermometry[J]. Proceedings, 2009:1235-1238.

[4] Wang F, Dong Z, Chen S, et al. Fast Temperature Estimation from Undersampled k-Space with Fully-Sampled Center for MR Guided Microwave Ablation.[J]. Magnetic Resonance Imaging, 2016, 34(8):1171-1180.

Figures

Figure. 1. Illustration of the framework of the proposed method. Low resolution images obtained from oversampled k-space center are used to calculate the multi-baseline weights and polynomial coefficient vector in the fast k-space hybrid model. Temperature-induced phase shifts are calculated by minimizing the cost function.

Figure. 2. Phantom heating simulation. a: The magnitude maps of the phantom and the full-sample CG reconstructed temperature are shown as references. b: Comparison of the reconstructed error maps using GA radial sampling at different acceleration factors. Corresponding root-mean-square errors (RMSEs) of the heated region-of-interest (ROI) are presented on each reconstructed error map.

Figure. 3. In-vivo liver experiment: a: The magnitude map of the liver marked with the location of ROI and the simulated temperature map are shown as references. b: Comparison of the fast k-space temperature reconstruction obtain from a golden angle radial data converted from Cartesian sampling using NUFFT with the full-sampled CG reconstruction. The RMSE of both methods are shown on the error maps. The improved accuracy of the proposed method demonstrates the effectiveness of hybrid model for motion correction.

Figure. 4. In-vivo spine experiment. a: The magnitude map of the spine image marked with the location of ROI and the simulated temperature map work as references. b: Comparison of Fast k-space reconstruction using GA radial sampling with the full-sampled CG reconstruction.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
2591