2590
An Adaptive Non-Local Denoising Method for Real-Time MR-Thermometry1University Medical Center Utrecht, Utrecht, Netherlands, 2University of Bordeaux, Bordeuaux, France
Synopsis
MR-guided targeted thermal therapies often rely on temperature information provided by proton resonance frequency shift (PRFS) thermometry. However, fast MR acquisition schemes are usually employed, in order to provide temperature updates with a short latency. This may lead to noisy temperature measurements, which can have a direct impact on therapy control and monitoring. In the current study we propose a novel non-local denoising technique for real-time MR-thermometry that improves data precision, while at the same time maximizing output accuracy, feature which is not guaranteed by currently employed real-time MR-temperature denoising methods.
Purpose
MR-guided targeted thermal therapies such as laser, radiofrequency (RF) and/or high intensity focused ultrasound (HIFU) ablations or hyperthermia, often rely on temperature information provided by proton resonance frequency shift (PRFS) thermometry1. However, fast MR acquisition schemes are usually employed, in order to provide temperature updates with a short latency. This may lead to noisy temperature measurements, which can have a direct impact on therapy control and monitoring. Previous studies have addressed this issue through various denoising solutions, which focused on improving temperature data precision without, however, making any guarantees on output accuracy. In the current study we propose a novel non-local denoising technique for real-time MR-thermometry that improves data precision, while at the same time maximizing output accuracy. The method was validated and compared to two widely used MR-thermometry filtering methods (one operating in the spatial and the other in the temporal domain) during an ex-vivo RF experiment carried-out on a calf liver.Methods
The denoising method proposed in the current study used as a starting point the non-local solution proposed by Buades2. The latter was adapted to real-time thermometry in the following manner3:
$$T_f\left(\vec{r_i},t\right)=\sum_{n=0}^{N-1}{\sum_{j\in\Omega}{w\left(\vec{r_i},\vec{r_j},t-n\right)T_m\left(\vec{r_j},t-n\right)}}\qquad\qquad\qquad \mathrm{(1)}$$
with
$$w\left(\vec{r_i},\vec{r_j},t-n\right)=\frac{1}{Z_i}\mathrm{exp}\left(-\frac{\|T_m(N_i, t)-T_m(N_j, t-n)\|^2}{2 \beta\hat{\sigma}(\vec{r_i})^2 |N_i|}\right)\qquad \mathrm{(2)}$$
where $$$T_f$$$ is the denoised temperature, $$$T_m$$$ are the noisy temperature measurements, $$$\|\cdot\|$$$ is the Euclidean norm, $$$\vec{r}_i$$$ and $$$\vec{r}_j$$$ are image spatial coordinates, $$$t$$$ is the image temporal index, $$$N_i$$$ and $$$N_j$$$ are local neighborhoods surrounding $$$\vec{r}_i$$$ and $$$\vec{r}_j$$$, $$$\Omega$$$ is the image domain, $$$|N_{i}|$$$ is the number of pixels in $$$N_{i}$$$, $$$N$$$ is the size of a temporal window encompassing the most recent $$$N$$$ temperature maps, $$$\hat{\sigma}(\vec{r}_i)$$$ is a local approximation of the noise standard deviation and $$$\beta$$$ is a free parameter. Output data accuracy was maximized by optimizing the value of $$$\beta$$$.
Accuracy of the filtered data was evaluated on a pixel-by pixel basis via the temperature bias expressed by Eq.(3). Considering that the temperature maps are altered by Gaussian noise, for ideally filtered temperature maps, $$$\epsilon(\vec{r})$$$ is a Gaussian variable with standard deviation $$$\sigma_e(\vec{r})$$$ (see Eq.(4)), having 95% of the values complying with $$$\left| \epsilon\left(\vec{r}\right)\right|\leq 2\sigma_{e}(\vec{r})$$$. Thus, in order to guarantee output accuracy, $$$2\sigma_{e}(\vec{r})$$$can be taken as an upper bound for $$$|\epsilon(\vec{r})|$$$. In effect, $$$\beta$$$ was optimized via the constrained optimization problem illustrated in Eq.(5).
$$\epsilon\left(\vec{r}\right)=\frac{1}{N}\sum_{n=0}^{N-1}\left[T_m(\vec{r},t-n)-T_{f}(\vec{r},t-n)\right]\qquad \mathrm{(3)}$$
$$\sigma_e(\vec{r})=\frac{1}{N}\sqrt{\sum_{n=0}^{N-1}{\hat{\sigma}}(\vec{r}, t-n)^2}\qquad\qquad\qquad\qquad \mathrm{(4)}$$
$$\hat{\beta}\left(\vec{r}\right)=\mathrm{argmax}_{\left\{\beta,\left|\epsilon\left(\vec{r}\right)\right|\leq 2\sigma_{e}(\vec{r})\right\}}\left|\epsilon\left(\vec{r}\right)\right|\quad\qquad\qquad \mathrm{(5)}$$
The method was validated on MR-thermometry data resulting from an ex-vivo MR-guided RF ablation in a calf liver, consisting in the delivery of 20 W of RF power over a duration of 50 s. During the procedure MR-data optimized for a high signal-to-noise ratio was acquired (used as a gold standard). Noise was then artificially added to the data. The proposed method was then applied to the noisy data, together with two widely used other methods for comparison: a Gauss spatial filter of size 3x3 and σ = 0.5 and a 5th order Cauer infinite impulse response (IIR) temporal filter4-5. For all methods, a multi-thread C++ implementation (8 threads) was carried-out.
Results and Discussion
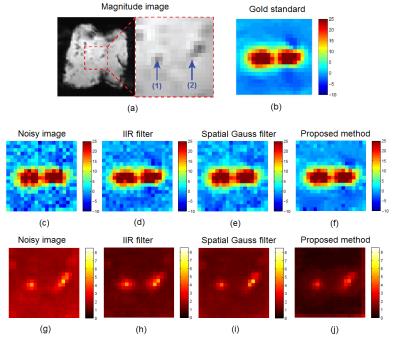
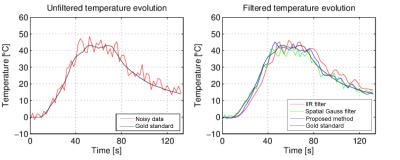
Fig.1(a) illustrates a magnitude MR-image of the calf liver together with the position of the bipolar RF needle (blue arrows). Fig.1(b)-1(f) display the temperature distribution in the heated area ~40 s into the therapeutic energy delivery in its original, noisy and its filtered versions, respectively. Fig.1(g)-1(j) showcase the temporally averaged absolute temperature errors introduced by the noise itself and each of the compared denoising methods. It can already be observed from the error maps that the proposed method outperforms the existing ones. This is further confirmed by the analyzing the temperature evolution at focal spot #1 from Fig.1(a), which is displayed in Fig.2. Note that the temporal lag of the IIR filter and the smoothing effect of the spatial Gauss introduce accuracy errors in the filtered data, effects that are minimal for the proposed method. Concerning computational demands, the proposed method required on average 311 ms. This is more than sufficient for respiratory-gated applications, which is the current standard for respiratory motion compensation during targeted thermal therapies.Conclusion
Accurate and precise temperature measurements are paramount for proper therapy control and endpoint detection during real-time MR-guided targeted thermal therapies. In the current work we propose a real-time non-local filtering technique dedicated to improving temperature measurements for such applications. Compared to other denoising methods previously employed during real-time MR-thermometry, the proposed approach has shown a considerable improvement in output accuracy, without introducing additional latency to the measured information. This, together with its low computational demands, demonstrates the potential of the method for use during real-time MR thermometry dedicated to targeted thermal therapies.Acknowledgements
This work was supported by the Dutch Technology Foundation (STW) (project OnTrack #12813) and in part by the European Research Council (project ERC-2010-AdG-20100317, Sound Pharma) and ITEA 2 (project SoRTS).References
1. V. Rieke and K. B. Pauly, “MR-thermometry,”, J Magn Reson Imaging, vol. 27, no. 2, pp. 376-390, 2008.
2. A. Buades et al, “A review of image denoising algorithms, with a new one,” J Multiscale Model Simul, vol. 4, no. 2, pp. 490 – 530, 2005.
3. C. Zachiu et al, "An Adaptive Non-Local-Means Filter for Real-Time MR-Thermometry," IEEE TMI, 2016, In press.
4. B. Denis de Senneville et al, “A direct PCA-based approach for real-time description of physiological organ deformations,” Int J Radiat Oncol Biol Phys, vol. 34, no. 4, pp. 974 – 982, 2015.
5. M. Ries et al, “Real-time 3D target tracking in MRI guided focused ultrasound ablations in moving tissues,” Magnetic Resonance in Medicine, vol. 64, pp. 1704 – 1712, 2010.
Figures