2552
The Role of Node Strength in Investigating Pathology1Institute of Neurology, University College London, London, United Kingdom, 2Department of Medical Physics and Biomedical Engineering, University College London, London, United Kingdom, 3Translational Imaging Group, Centre for Medical Image Computing, Department of Medical Physics and Biomedical Imaging, University College London, London, United Kingdom, 4Medical Statistics Department, London School of Hygiene and Tropical Medicine, London, United Kingdom, 5National Hospital of Neurology and Neurosurgery, London, United Kingdom, 6Institute of Child Health, University College London, London, 7Department of Brain and Behavioural Sciences, University of Pavia, Pavia, Italy, 8Brain MRI 3T Mondino Research Center, C. Mondino National Neurological Institute, Pavia, Italy
Synopsis
Graph theoretical network properties, while successful in exploring topological features of entire brain networks, have limited sensitivity to localized disease effects. This work explores the role of node strength as an objective way to characterize disease. Differences in the default mode network (DMN) between a cohort of relapsing-remitting multiple sclerosis (RRMS) patients and healthy controls (HC) have been explored using standard graph metrics (e.g. efficiency) and node strength. No differences in graph metrics were observed between the groups; however several key regions of the DMN had a significantly reduced strength in RRMS than HC (5% significance level).
Purpose
Graphs representing brain networks are useful for visualizing connectivity and exploring the effects of different pathologies beyond localized damage. Graph theory provides composite measures that encapsulate topological properties of the whole network, and has successfully demonstrated disrupted connectivity in a range of diseases1,2,3. Graph theoretical properties are directly dependent on connection (edge) locations and weights; however, because information is typically condensed into a single measure, some local information (for instance which regions and connections are most affected in pathologies) is lost. As a result, the sensitivity of these properties to subtle, localized disease effects is reduced. It is possible to examine the integrity of each edge individually (e.g. number of streamlines of a connection), or a property of the node itself (e.g. cortical thickness) and investigate the correspondence with clinical outcomes.
Crucially, neither graph theoretical properties nor individual edges are able to capture the possible cascade effect that several damaged edges may have on a specific node. While centrality measures, for instance, are based on the presence or absence of a connection, it may be that connection integrity, and the identification of nodes that are impaired by one or more damaged connection, is more informative.
This work is an exploratory study to assess the validity of a property less explored, i.e. node strength, obtained by assigning to each node the composite weight of all its connected tracts. This approach has the advantage of retaining local information while reducing the need for excessive multiple comparisons unavoidable when testing individual edges. Moreover it could highlight nodes that, while not directly affected by the disease, may be connected to several affected edges; these nodes may then become pivotal in disease mechanisms. The various levels of analyses (graph topological properties, individual edge weights and node strength) are applied in a pilot study of relapsing-remitting multiple sclerosis (RRMS) patients and healthy controls (HCs).
Methods
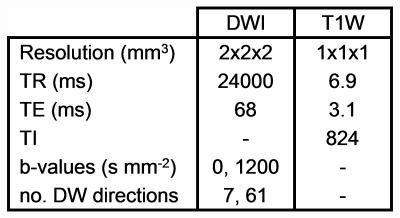
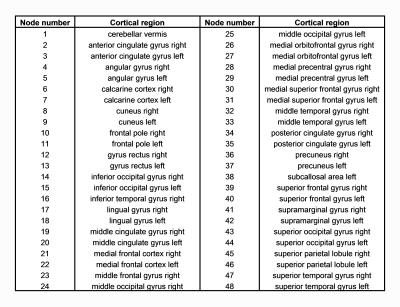
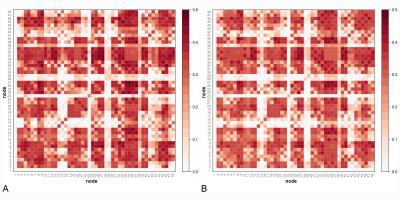
Data from 23 HCs (14 female; mean age 37.9 ± 12.6 years) and 22 RRMS patients (18 female; mean age 42.8 ± 10.7 years; mean disease duration 14.0 ± 8.4 years; median EDSS score 2.0) were recruited. Diffusion-weighted (DW) and T1-weighted images were acquired using an Achieva 3T MR scanner (Philips Healthcare, Best, Netherlands) with a 32-channel head coil (Table 1). Tractography was performed between 48 regions generated from a parcellation4,5 in and around the default mode network (DMN) using TractoR6 (Table 2 gives correspondences between node number and parcellation); average group-wise brain graphs, weighted using fractional anisotropy (FA), were created (Figure 1).
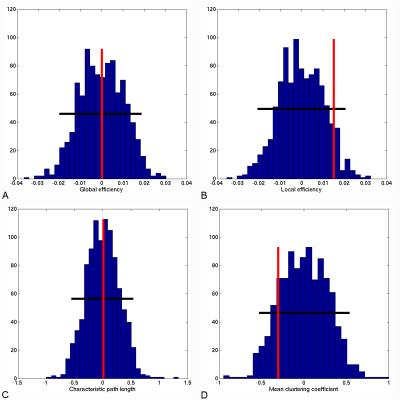
A non-parametric permutation test was adopted7 to investigate network differences between groups. Differences in topological properties (global and local efficiency, mean clustering coefficient and characteristic path length), individual edge weights and node strengths were explored.
Results
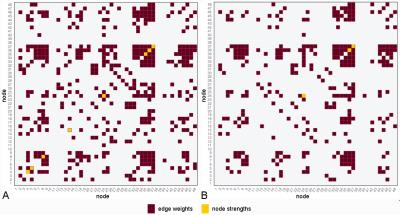
No differences in the topological properties of HC and RRMS networks were seen (at 5% significance level) (Figure 2); however approximately 23% of edge weights were found to be significantly different between groups (Figure 3a), 19% of which remained significant at 1% significance level (p<0.01) (Figure 3b).
When considering node strength, eight specific regions demonstrated a significant difference (strength lower in RRMS) between groups at 5% significance level (Figure 3).
Discussion
Graph properties of RRMS patients were not altered compared to HCs in this cohort, possibly reflecting the minimal disability of the RRMS group; individual edge weights, though, demonstrated sensitivity to disease effects. Interestingly, several nodes with different strength characteristics between groups correspond to core DMN regions8, such as the posterior cingulate gyrus (node 35) and precuneus (nodes 36, 37). These are densely connected areas with a higher probability to be linked to damaged edges.
A key feature of this approach is to be objective in assessing damage. Future work will explore node strength using several weights and MS subtypes, correlating node strength and lesion topology.
Conclusions
Connectivity in the DMN has been investigated using standard graph metrics, individual edge weights and node strengths. In a population of minimally disabled RRMS patients it was demonstrated that overall graph properties are not sensitive to subtle pathological processes, but that edge properties (e.g. FA) can be altered by pathology compared to HCs. Further, by integrating edge information into a measure of node strength, it is possible to objectively extract a subset of nodes that may play a pivotal role in the disease. Future studies in MS and other neurological conditions could confirm the utility of such measures as imaging biomarkers of disease, providing complementary information to network-wise properties or a priori identified local metrics, i.e. in or around lesions.Acknowledgements
This work is supported by the EPSRC-funded UCL Centre for Doctoral Training in Medical Imaging (EP/L016478/1) and the Department of Health’s NIHR-funded Biomedical ResearchCentre at University College London Hospitals. The authors also thank the UK MS Society for generous support to the NMR Research Unit, Queen Square MS Centre.References
1. Bassett DS, Bullmore E, Verchinski BA, et al. Hierarchical organization of human cortical networks in health and schizophrenia. J Neurosci. 2008;28(37):9239-9248.
2. Rocca MA, Valsasina P, Meani A, et al. Impaired functional integration in multiple sclerosis: a graph theory study. Brain Struct Funct. 2016;221:115-131.
3. Cao Q, Shu N, An L, et al. Probabilistic diffusion tractography and graph theory analysis reveal abnormal white matter structural connectivity networks in drug-naive boys with attention deficit/hyperactivity disorder. J Neurosci. 2013;33(26):10676-10687.
4. Cardoso MJ, Modat M, Wolz R, et al. Geodesic information flows: spatially-variant graphs and their application to segmentation and fusion. IEEE Trans Med Imaging. 2015;34:1976-1988.
5. Prados F, Cardoso MJ, Burgos N, et al. NiftyWeb: web based platform for image processing on the cloud. Singapore: International Society for Magnetic Resonance in Medicine (ISMRM) 24th Scientific Meeting and Exhibition; 2016.
6. Clayden JD, Maniega SM, Storkey AJ, et al. TractoR: magnetic resonance imaging and tractography with R. J Stat Softw. 2011;44:1-18
7. Bullmore ET, Bassett DS. Brain graphs: graphical models of the human brain connectome. Annu Rev Clin Psychol. 2011;7:113-140.
8. Buckner RL, Andrews-Hanna JR, Schacter DL. The brain’s default network: anatomy, function and relevance to disease. Ann N Y Acad Sci 2008;1124:1-38
Figures