2548
Noise reduction with TGV, Gaussian and Wiener filtering methods in FLAIR² imagesRené Schranzer1, Alexander Rauscher2, Evelin Haimburger1, Kristian Bredies3, Gernot Reishofer4, and Günther Grabner1,5
1Department of Radiologic Technology, Carinthia University of Applied Sciences, Klagenfurt, Austria, 2UBC MRI Research Centre, University of British Columbia, Vancouver, Canada, 3Institute for Mathematics and Scientific Computing, University of Graz, Graz, Austria, 4Department of Radiology, Medical University of Graz, Graz, Austria, 5Institute for Applied Research on Ageing, Carinthia University of Applied Sciences, Klagenfurt, Austria
Synopsis
The reduction of noise is of high value for FLAIR² images because the multiplication of FLAIR and T2 images will always result in an image with a reduced Signal-to-noise-ratio. Here different filter methods, like Gaussian, Wiener and Total Generalized Variation were used to demonstrate noise reduction. The drawback of noise reduction is a blurring effect of anatomical structures. In this study we demonstrate that TGV filtering has certain advantages compared to Wiener and Gaussian techniques in research and clinical applications.
Purpose:
To improve multiple sclerosis (MS) research, a new imaging contrast was developed, namely, the combination of FLAIR and T2-weighted data called FLAIR².1 To create FLAIR² images, FLAIR and T2-weighted images are multiplied which reduces the Signal-to-noise-ratio (SNR). The reduction of noise is therefore of high value for FLAIR². The recently developed total generalized variation (TGV) method has favorable abilities in terms of edge preservation and noise removal.² This study aims to demonstrate noise reduction of using TGV filtering compared to Gaussian and Wiener filtering methods in FLAIR² images. For FLAIR², this means that denoising the FLAIR, the T2 or both may improve the resulting FLAIR² images.Methods:
In this study T2-weighted and FLAIR data of two MS patients were used – details can be found in Wiggermann et al.1 Before image combination and analysis all datasets (FLAIR, T2) were registered into a common image space, using a linear approach with 6 degrees of freedom using the MINC-tools.³ Afterwards TGV, Gaussian and Wiener filtering was applied to T2, FLAIR and the native (no filtering) FLAIR². We started with moderate filter parameters and increased values step by step until noise was sufficient eliminated in the resulting image. Within this work, the following filter parameters were used: Wiener: kernel size 3.2 mm; Gaussian: FWHM 3.53 mm and TGV: automatic evaluation of regularization parameter with 11% noise assumed for FLAIR/FLAIR² and 5% noise assumed for T2 with 100 iteration steps. Additionally FLAIR² images were created using all combinations of input data (FLAIR.denoised multiplied T2, FLAIR.denoised multiplied T2.denoised, FLAIR multiplied T2.denoised). SNR and contrast-to-noise (CNR) measurements were performed using the subtraction method as described in [1] for all FLAIR² derivatives and for ten MS lesions.Results:
FLAIR² images filtered with TGV show the highest SNR and CNR, while SNR values are similar for Gaussian and Wiener filtered images. The average CNR over 10 lesions within the native FLAIR² (34.89) achieved an improvement to 97.4, 84.4 and 58.27 corresponding to TGV, Wiener and Gaussian filtering. In contrast, FLAIR multiplied with T2.denoised shows no improvement, while FLAIR.denoised multiplied with T2 shows an increase by a factor of two to the native, no filtered FLAIR². Detailed SNR and CNR values are shown in Table 1. Figure 1 gives an example for noise reduction in homogeneous white matter using the mentioned filtering techniques. The drawback of noise reduction is the accompanied low-pass effect on the resulting images which is more apparent for larger filter kernels. Figure 2 demonstrates that effect on a single MS lesion. Therefore, an alternative to the TGV filtered FLAIR² which shows the highest SNR and CNR value is the combination of T2 multiplied with FLAIR.denoised. This approach has the advantage that high frequency components are untouched in the T2 images which results in a better definition of brain structures - Figure 3 shows that effect.Discussion:
The multiplication of two images will always result in an image with reduced SNR compared to the SNR of the two input images.1 However, filtering with appropriate noise reduction methods, such as TGV, Gaussian or Wiener, can rise the SNR again. But, applying noise reduction has always a low-pass effect on the resulting images (Figure 2). A very promising combination next to the TGV filtered FLAIR² might therefore be the combination of T2 images with FLAIR.denoised images. An advantage of this method is more preserved edge information as T2-weighted image are not low-pass filtered.Conclusion:
Gaussian filtering reduces image noise as well as Wiener filtering, but this method has one disadvantage. Gaussian filtering tends to blur edges and therefore lesions borders more compared to TGV and Wiener filtering. The Wiener and TGV methods preserve edges and visualize image details with reduced noise. For clinical practice, the TGV-filtered FLAIR multiplied with T2 should be the first choice to create FLAIR² images as they show a more natural look combined with sharper edges while TGV-filtered FLAIR² images look more plastically.Acknowledgements
No acknowledgement found.References
1. Wiggermann V, Hernandez-Torres E, Traboulsee A, et al. FLAIR²: A Combination of FLAIR and T2 for Improved MS Lesion Detection. AJNR Am J Neuroradiol. 2016;37(2):259-265. 2. Bredies K, Kunisch K & Pock T. Total Generalized Variation. Siam J Imaging Sci. 2010;3(3):492-526. 3. Vincent RD, Janke A, Sled JG, et al. A Modality independent format for multidimensional medical images. 2004:Proceedings of the 10th Annual Meeting of the Organization for Human Brain Mapping.Figures
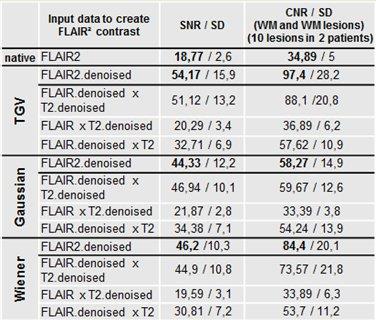
Table 1. Mean SNR and CNR values for the
different FLAIR² creation methods.
Note: The table can be split into four sections: first the native input data
and
second to fourth after filtering (TGV, Gaussian & Wiener). SNR and
CNR values are shown for all combination possibilities. Note that filtered
data are marked by the ending “.denoised”.
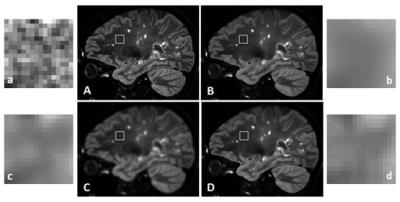
Figure 1. Comparison of different filtering
techniques on a FLAIR² image: (A) native FLAIR² image, (B) TGV filtered image,
(C) Gaussian filtered image and (D) Wiener filtered image, a-d represent sub
regions of A-D marked with the white rectangle. The windowing of all sub
regions is identical (image mean ± 30%) in order to demonstrate noise
reduction. Note that (b) TGV exhibit the best result after filtering (image
standard deviation (SD) 0.140), Gaussian (c) and Wiener (d) filtering show similar
results namely SD 0.148 and SD 0.151 respectively. The SD in the native FLAIR²
image (a) is 0.357.
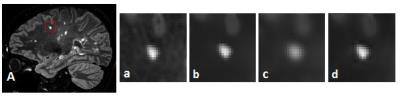
Figure 2. Noise reduction and
blurring: A sagittal FLAIR² image of an MS patient. a-d represent sub regions
of A for the different filtering techniques (a) original FLAIR², (b) TGV, (c)
Gaussian and (d) Wiener filtering. As can be seen the blurring effect is most
prominent for the Gaussian filtering. TGV and Wiener filtering show similar blurring
affects.
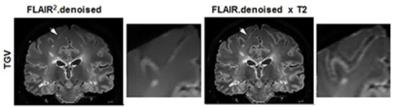
Figure 3. Comparison of edge information on
a sulci (white arrow): The FLAIR.denoised x T2 image (right) shows a sharper
appearance compared to the filtered FLAIR² (left).