2537

Gaining insights into Multiple Sclerosis Lesion Characteristics from Brain Tissue Microstructure Information: A multi-compartment T2 relaxometry Approach

Sudhanya Chatterjee¹, Olivier Commowick², Simon K. Warfield³, and Christian Barillot⁴

¹VisAGeS, IRISA U746, Universite de Rennes-1, Rennes, France, ²VisAGeS Inserm U746, IRISA, Inria, Rennes, France, ³Boston Children’s Hospital, Boston, MA, United States, ⁴VisAGeS, INRIA/IRISA, Inserm U746, CNRS, Rennes, France

Synopsis

Clinical trends and Pathogenetic ways of onset and progression of Multiple Sclerosis (MS) in patients suggest that MS is a highly heterogeneous disease. MS is predominantly a White Matter (WM) disease, which is mainly composed of myelinated axons and neuroglia type cells. Demyelination and axonal loss characterize the condition of MS in a patient. However, they follow varying trends in patients. In this work, we propose a method in which T2 relaxometry data is used to obtain a quantitative brain tissue microstructure information. This information is then studied to check its corroborations with pathogenetic understanding of MS in literature.

Purpose

To propose a T2 relaxometry based multi-compartment model to gain insight into brain tissue microstructure. Hence improve understanding of MS from point of tissue microstructure information.

Background

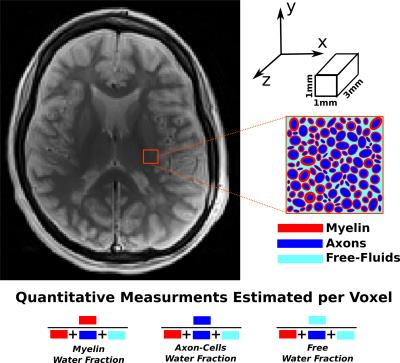
In this work, we approach the problem of characterization of MS as a white matter disease. Hence we focus on quantifying the condition of axons and myelin in the brain tissues. Myelin is a tightly wrapped structure around the axons and has very high lipid contents (70−80% by dry weight)¹ distinguishing it from other tissues. It is also a relatively dehydrated structure (~40% water content)¹. These molecular properties of Myelin are responsible for it having a very short T2 relaxation rate compared to other brain tissues as axons, gray matter cells and fluids (e.g.: CSF, water accumulation due to inflammation etc.). Tissues in brain can be broadly classified into three categories based on T2 relaxation rates: fast, medium and slow decaying components. MRI has limited resolution and hence the voxels are heterogeneous in terms of T2 relaxation rates of the tissues microstructures. In this work, we propose a multi-compartment T2 relaxometry model which helps visualize the tissue microstructure information in a quantitative framework (Figure-1). A straightforward model to represent the variety of T2 spin decays information in a voxel is to express each voxel as a weighted sum of predefined exponentially decaying curves^{2, 3}. However such an approach is feasible only for classical Hahn Spin Echo (SE) sequences, which suffer from the drawback of having long acquisition times. In this work, we use multi-contrast TurboSE technique where the acquisition time is fairly short for a desirable resolution.

Method

Unlike classical Hahn SE sequence, turboSE sequence data suffer from the effect of stimulated echoes⁴. The echo curves for such sequences can be computed using Extended Phase Graph (EPG) algorithm⁵. The T2 space is modeled as a weighted mixture of signal contributions from the three compartments. Each compartment is described as a Gaussian PDF in the T2 space. The multi-compartment T2 relaxometry signal model is formulated as:

$$s\left(t_i\right)=M_{0}\sum_{j=1}^{3}{w_j}{\displaystyle\int\limits_{T_2}}{\small{{f_j}\left(T_{2};\mu_j,\sigma_j\right)EPG\left(T_{2},\triangle{TE},i,T_1,B_1\right)dT_{2}}}$$

where $$$s(t_i)$$$ is the voxel signal at $$$i$$$-th echo time$$$\;(t_i)$$$.$$$\;{f_j}\left(T_{2};\mu_j,\sigma_j\right)\;$$$is the Gaussian PDF with mean and variance of$$$\;\mu_j\;$$$and$$$\;\sigma_j^2\;$$$respectively.$$$\,\mathrm{B_1}$$$:$$$\,$$$field inhomogeneity.

The cost function optimized for each voxel data series amounts to the following:

$$\min_{\mathbf{c},B_1}\parallel\mathbf{Y}-\mathbf{S}\parallel_2^2\;=\;\min_{\mathbf{c},B_1}\sum_{i=1}^{m}\left(y_i-\sum_{j=1}^{3}c_j{\displaystyle\int\limits_{T_2}}{\small{{f_j}(T_2)\;EPG(T_2,\triangle{TE},i,T_1,B_1)dT_2}}\right)^2$$

where$$$\;\mathbf{Y}$$$ is the observed signal.$$$\;\mathbf{Y},\;\mathbf{S}\in\mathbb{R}^m;\;\mathbf{c}\in\mathbb{R}^3;\;m=\;$$$number of echoes.$$$\;\mathbf{c}\;$$$is a vector of scaled weights:$$$\;c_j=M_0w_j,\;$$$from which the weights are obtained as:$$$\;w_j=c_j/\sum_i{c_i}.\;$$$The distribution parameters for the compartments are chosen in accordance with the information available based on the histology studies²:$$$\;\mu=\lbrace{20,10,2000}\rbrace,\;\sigma=\lbrace{5,10,80}\rbrace$$$.$$$\;\mathbf{c}\;$$$is computed by NNLS optimization. The$$$\;B_1\;$$$value is computed by a gradient free optimizer (BOBYQA⁷) post weights optimization as it doesn’t have any closed form solution⁵. We perform$$$\;\mathbf{c}\;$$$and$$$\;B_1\;$$$optimization alternatively till convergence is obtained in desired error limit. The proposed method was implemented in ITK (C++).

Result and Discussion

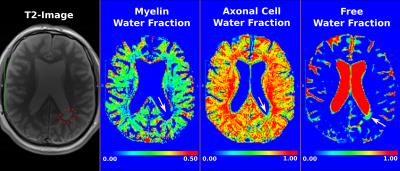
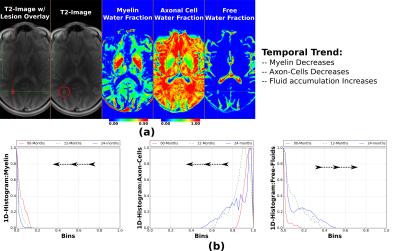
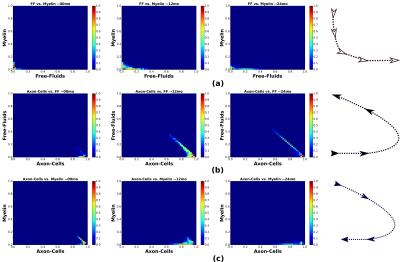
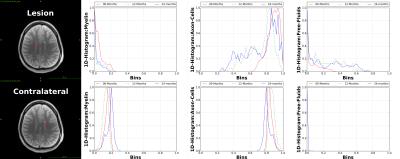
Data: SIEMENS Verio 3.0T; Multi-contrast TurboSE sequence; 11$$$\,$$$echoes, 1^st$$$\,$$$echo:$$$\,$$$8.4ms, Echo$$$\,$$$Spacing:$$$\,$$$8.4ms; Slice thickness:$$$\,$$$3mm, In$$$\,$$$plane$$$\,$$$resolution:$$$\,$$$1.3mmx1.3mm, Matrix Size:$$$\,$$$192x192; BW_acq$$$\,$$$=$$$\,$$$343Hz/px; TR:$$$\,$$$5240ms; T_acquisition$$$\,$$$=$$$\,$$$7min40sec. For every patient we acquire data at 0, 12 and 24 months time points. Experiment-1: We test the estimation algorithm on a patient data to observe its capability to distinguish between healthy and lesion regions of the brain. For the results of this experiment refer Figure-2. This is in line with the existing literature on pathogenetic studies of MS⁶. We perform a couple of additional experiments using the proposed method to study lesions in patients. Experiment-2: Here we observed the temporal trend of the microstructure representations in a lesion of a patient as quantified by the estimation framework. Results shown in Figure-3 suggest that the myelin and axonal-cell water fractions in the lesion reduce as we progress from the 0^thto the 24^th month, whereas fluid accumulation increases over the same period. A 2D-histogram (Figure-4) provides a visualization of how water fraction of a compartment changes with respect to another in line with existing literature^2,3,6. Experiment-3: We compare the quantitative estimation of water fractions of the compartments between a lesion and a contralateral healthy ROI (Figure-5). Both experimental observations are in accordance with observations in literature for Pathogenetic studies⁶ of MS. The water fraction and B1 estimation algorithm was tested on 5 patients (16 data-sets). We observe a diversity in water fraction statistics in intra- and inter-patients lesions. Hence, this method helps us visualize the heterogeneous nature of MS as stated in the literature^1,6.

Conclusion

The proposed T2 relaxometry multi-compartment model provides insights into the microstructure information of brain tissues in a quantitative framework. The observations of the experiments on patient data confirm those of existing literature^2,3,6. This provides motivation to explore such models for quantifying brain microstructure and gaining insights into neurodegenerative diseases such as MS.

Acknowledgements

MRI data acquisition was supported by the Neurinfo MRI research facility from the University of Rennes I. Neurinfo is granted by the the European Union (FEDER), the French State, the Brittany Council, Rennes.

References

1. M. van der Knaap and J. Valk, Magnetic resonance of myelination and myelin disorders. No. 3, Springer-Verlag Berlin Heidelberg, 2005.

2. C. Laule, I. M. Vavasour, S. H. Kolind, D. K. B. Li, T. L. Traboulsee, G. R. W. Moore, and A. L. MacKay, “Magnetic resonance imaging of myelin,” Neurotherapeutics, vol. 4, no. 3, pp. 460–484, 2007.

3. A. MacKay, C. Laule, I. Vavasour, T. Bjarnason, S. Kolind, and B. M¨adler, “Insights into brain microstructure from the T2 distribution,” Magnetic Resonance Imaging, vol. 24, no. 4, pp. 515–525, 2006.

4. J. Hennig, M. Weigel, and K. Scheffler, “Calculation of Flip Angles for Echo Trains with Predefined Amplitudes with the Extended Phase Graph (EPG)-Algorithm: Principles and Applications to Hyperecho and TRAPS Sequences,” Magnetic Resonance in Medicine, vol. 51, no. 1, pp. 68–80, 2004.

5. T. Prasloski, B. Madler, Q. S. Xiang, A. MacKay, and C. Jones, “Applications of stimulated echo correction to multicomponent T2 analysis,” Magnetic Resonance in Medicine, vol. 67, no. 6, pp. 1803–1814, 2012.

6. H. Lassmann, W. Bruck, and C. Lucchinetti, “Heterogeneity of multiple sclerosis pathogenesis: Implications for diagnosis and therapy,” Trends in Molecular Medicine, vol. 7, no. 3, pp. 115–121, 2001.

7. Powell, Michael JD. "The BOBYQA algorithm for bound constrained optimization without derivatives." Cambridge NA Report NA2009/06, University of Cambridge, Cambridge (2009).

Figures

Figure 1: Problem Description: Every Voxel is heterogeneous in nature. Proposed Quantitative measurements to assess the components of a voxel.

Figure 2: (L-R) Original T2-image. The region marked with red dotted line encloses a lesion. Note absence in myelin water fraction in the Lesion Region. For the water fraction corresponding to axon-cells. Reduced water fraction corresponding to axonal-cells can be observed in lesion region compared to neighboring healthy tissues. Accumulation of fluid can be observed in Lesion region which is otherwise absent in neighboring healthy tissues. These are all in agreement with the MS pathogenetic studies.

Figure 3: (a) Red circle in T2-image encapsulates the lesion region which is accurately represented by the red mask in left-most figure. The cross-hair is to aid in observation of the lesion ROI in all the images. In the lesion ROI quantitative estimations show absence of water fraction corresponding to Myelin, reduction in water fraction corresponding to axons compared to healthy tissues neighboring lesion and fluid accumulation which is otherwise absent in neighboring healthy tissues. (b) Distribution of compartmental water-fraction in the lesion region. Note the temporal trend is in agreement with pathological trends noted in the literature.

Figure 4: 2D-histograms of the Lesion shown in Fig 3. Histograms suggest: (a) Myelin reduction accompanied by Fluid accumulation. (b) Fluid accumulation accompanied by reduction in axon-cell water-fraction representation (c) Reduction of both Myelin and axon-cell-water fraction representation over time.

Figure 5:Temporal Trend of Lesion vs Healthy Contra-lateral ROI. (Top) Lesion's 1D histograms follow pattern as discussed in Fig 3. (Bottom) For healthy contra-lateral RoI distributions remain unchanged w/ complete absence of fluid accumulation.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

2537