2511
Optimization of Quantitative Magnetization Transfer Imaging for Accurate PSR Estimation in the Spinal Cord1Department of Electrical Engineering, Vanderbilt University, Nashville, TN, United States, 2Vanderbilt University Institute of Imaging Science, Vanderbilt University, Nashville, TN, United States, 3Department of Radiology and Radiological Sciences, Vanderbilt University Medical Center, Nashville, TN, United States
Synopsis
Quantitative magnetization transfer (qMT) sampling schemes typically attempt uniform sampling of the MT z-spectrum but this may not be optimal for PSR estimation of the human spinal cord in vivo. We utilize Monté Carlo simulations of fitting synthetic qMT data to produce an optimal sampling scheme of the MT z-spectrum. This sampling scheme is evaluated in a healthy control and compared to current best practices where we see superior PSR estimation with our optimized sampling scheme.
Introduction
Quantitative magnetization transfer (qMT) sampling schemes have not changed drastically since the earliest implementations and have been based off uniform sampling of the MT z-spectrum1,2,3. Previous work attempted to numerically optimize qMT of the brain through numerical propagation of error, but similar studies have not been attempted to obtain robust estimates of qMT-derived indices in the human spinal cord4. In this work, we use Monte Carlo fitting of simulated data to optimize a qMT acquisition protocol to improve the accuracy of the pool-size ratio (PSR) estimation in the human spinal cord in vivo.Methods
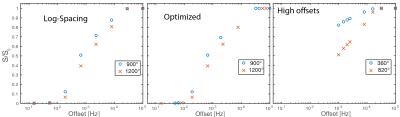
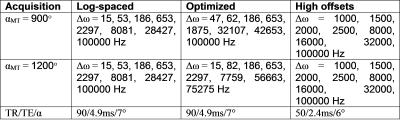
Optimization: To optimize the sampling scheme for MT z-spectra, we started with a log-linearly spaced sampling scheme and iteratively swapped points with those from a denser sampling scheme, accepting the permutation with the lowest PSR mean squared error. The initial model comprised of 8 offset frequencies evenly distributed in log-space from 15Hz – 100kHz at two RF MT saturation powers, 900° and 1200°. A denser sample set of 32 offsets at these same two powers were generated as possible sampling points. The swapping of each original point was evaluated iteratively using the mean squared error of PSR estimation of each potential model using 10,000 Monté Carlo simulations of Gaussian random noise at SNR=100. The best performing swap (or the original model) was chosen and the next point was then evaluated. Once all 16 points in the original model had been evaluated for superior performance, the final model consisted of the sampling scheme in Table 1, column 2. Figure 1 shows a graphical representation of the three sampling schemes evaluated including the original starting scheme (left) and the optimized scheme (middle).
Acquisition: One healthy volunteer was imaged using a 3.0T Achieva whole body scanner (Philips, The Netherlands). A two-channel transmit body coil was used for excitation and a 16-channel SENSE neurovascular coil for reception. A volume centered near C2-C3 was selected from a T2-weighted survey image. qMT data were acquired over this volume using a 3D MT-prepared spoiled gradient echo sequence3. MT-preparation used a 20ms single-lobe sinc-Gauss pulse, saturation flip angle (αMT) and offset frequencies (Δω) as well as other imaging parameters prescribed in Table 1, FOV=150x150x60mm3 , resolution = 1.0x1.0x5.0mm3, 2 signal averages. B1 was measured in the same volume using the actual flip angle imaging method TR1/TR2=30/130ms, α=60°)5; ΔB0 from gradient echo phase images acquired (ΔTE=2.3ms)6; and T1 using a multiple flip angle (MFA) acquisition (TR/TE=20/4.6ms, α=5, 10, 15, 20, 25, 30°). A high-resolution (0.65x0.65x5.0mm3) multi-echo gradient echo (mFFE) anatomical image was also acquired for registration (TR/TE/ΔTE=700/6.5/8.2 ms, α=28°). Total scan time for all three sampling schemes and accompanying scans was 44 minutes.
Processing: All image volumes were coregistered to the MFA to correct for motion artifacts using reg_aladin from niftyreg7. Measurements were normalized to the highest offset acquired (>70kHz) and fit to a two-pool model2 of the MT effect also using MFA, B1 and B0 maps for correction of field inhomogeneities and T1 variations. Gray matter (GM) and white matter (WM) was manually labeled on the mFFE scan and propagated to each of the qMT fits for comparison of PSR contrast.
Results
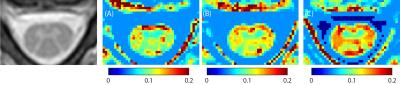
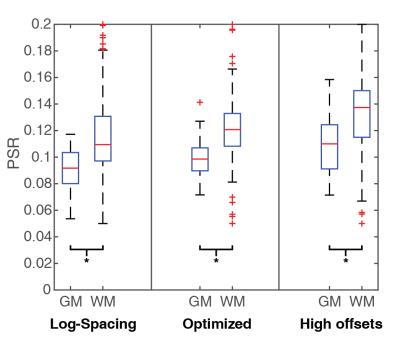
Figure 2 shows the anatomical mFFE (left) as compared to the PSR maps generated from the log-spaced sampling scheme (A), optimized sampling scheme (B) and high offsets sampling scheme which avoids lower offsets nearer to water (C). Qualitatively the PSR map in (B) using the optimized sampling scheme presents the best visualization of the spinal cord GM butterfly seen in the mFFE. Figure 3 shows a comparison of PSR for both GM and WM. For all three methods PSR was significantly different between GM and WM by Wilcoxon rank-sum (p<0.01). The optimized sequence shows lower variance within WM than the other two methods while maintaining the superior contrast of the high offsets approach.Conclusions
Initial results are promising that numerical optimization of qMT sampling for the purpose of improved PSR fitting in the spinal cord is possible while more empirical evaluation is necessary. Further evaluation in patient populations are necessary to understand the sensitivity to MT phenomenon in pathology.Acknowledgements
Research reported in this publication was supported in part by the National Institutes of Health R21EY024036, R01EY023240 and 5T32EY007135. This work was conducted in part using the resources of the Advanced Computing Center for Research and Education at Vanderbilt University, Nashville, TN. The authors would also like to thank Samantha By and Alex K Smith for their help with this work.References
1. Mossahebi, Pouria, et al. "Removal of cerebrospinal fluid partial volume effects in quantitative magnetization transfer imaging using a three-pool model with nonexchanging water component." Magnetic resonance in medicine 74.5 (2015): 1317-1326.
2. Yarnykh, Vasily L., and Chun Yuan. "Cross-relaxation imaging reveals detailed anatomy of white matter fiber tracts in the human brain." Neuroimage 23.1 (2004): 409-424.
3. Sled, John G., and G. Bruce Pike. "Quantitative imaging of magnetization transfer exchange and relaxation properties in vivo using MRI." Magnetic resonance in medicine 46.5 (2001): 923-931.
4. Levesque, Ives R., John G. Sled, and G. Bruce Pike. "Iterative optimization method for design of quantitative magnetization transfer imaging experiments." Magnetic resonance in medicine 66.3 (2011): 635-643.
5. Yarnykh, Vasily L. "Actual flip-angle imaging in the pulsed steady state: a method for rapid three-dimensional mapping of the transmitted radiofrequency field." Magnetic resonance in Medicine 57.1 (2007): 192-200.
6. Skinner, Thomas E., and Gary H. Glover. "An extended two-point dixon algorithm for calculating separate water, fat, and B0 images." Magnetic resonance in medicine 37.4 (1997): 628-630.
7. Ourselin, Sébastien, et al. "Reconstructing a 3D structure from serial histological sections." Image and vision computing 19.1 (2001): 25-31.
Figures