Synopsis

Microstructural changes of the corticospinal tract (CST) in idiopathic normal pressure hydrocephalus (iNPH) before and after CSF shunt surgery were studied using NODDI and WMTI. Pathological increase of orientational coherence and its postoperative normalization were shown, indicating axon stretching and its recovery. To the contrary, decrease of axon density was present in iNPH and remained after the surgery. Simulation using undulating cylinder model demonstrated both NODDI and WMTI can separate the effects from axon density and undulation. These results suggest possibilities of diffusion MRI to distinguish between reversible and irreversible microstructural changes in iNPH, and raise expectation for prediction of treatment outcome.

Purpose

This study aimed to investigate the post-operative changes of microstructural properties within the corticospinal tract (CST) in idiopathic normal pressure hydrocephalus (iNPH), using NODDI¹ and WMTI².

iNPH is a geriatric disease characterized by the triad of gait disturbance, dementia, and urinary incontinence. Though iNPH is treatable by CSF shunt surgery, the degree of improvement varies considerably among different series and there is a need for quantitative markers that reflect disease severity and irreversibility. By conventional DTI, FA increase in the CST was reported as unique phenomenon in iNPH and has been speculated as axon stretching^3,4. However, reports on correlation with symptom severity and/or treatment outcome are limited. Biophysical modeling of diffusion MRI, like NODDI and WMTI, is expected to provide insights into the underlying microstructure, as it infer more specific tissue properties than DTI.

For now, both NODDI and WMTI model axons as straight sticks and do not explicitly account for axon stretching/undulation, which implies the accuracy of the output parameters in the presence of undulation and/or their sensitivity to stretching/undulation are unknown. To grasp the effect of stretching/undulation on NODDI and WMTI metrics, simulation experiment using undulating cylinder model was also performed.

Methods

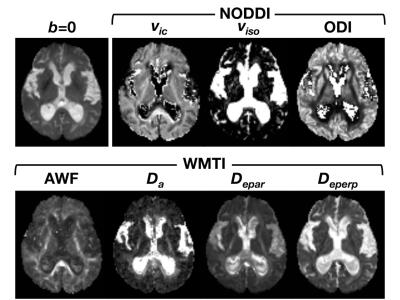
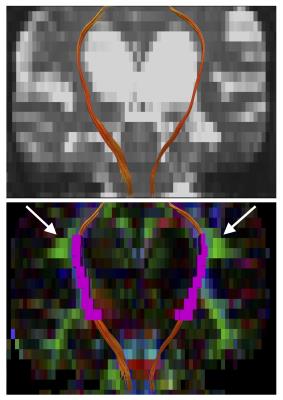
Human data: Diffusion MRI data was acquired with a 3-T unit in 10 iNPH patients and 14 age-matched controls, using a SE-EPI sequence with 5 diffusion weightings (b = 500, 1000, 1500, 2000, and 2500 s/mm²) along 32 noncolinear directions, and 1 b=0 s/mm² volume. The publicly available toolboxes were used for calculation of NODDI (https://www.nitrc.org/projects/noddi_toolbox) and WMTI (https://github.com/NYU-DiffusionMRI/Diffusion-Kurtosis-Imaging). Examples of the output maps are shown in Fig 1. To make intuitive comparison between NODDI and WMTI, some translation was made to the output metrics⁵. From the definition of NODDI’s 3-compartment, AWF in NODDI is expressed as $$$f_{ic}(1-f_{iso})$$$. For WMTI, estimation of the dispersion is represented as: $$$\tau_{1}=\langle cos^{2}\psi\rangle =\frac{D_{a,1}}{Tr(\overline{D_{a}})}$$$, where $$$\psi$$$ is the angle of dispersion around the main axis. For NODDI, the relationships between ODI and $$$\tau_{1}$$$ is expressed as: $$$ODI=\frac{2}{\pi}arctan(1/\kappa), \tau_{1}=-\frac{1}{2\kappa}+\frac{1}{\sqrt{\pi}e^{-\kappa}erfi(\sqrt{\kappa})\sqrt{\kappa}}$$$, where $$$\kappa$$$ is the concentration parameter of Watson distribution. $$$\tau_{1}$$$ varies from 1/3 for isotropically dispersed orientation to 1 for strictly parallel orientation. Tract-specific analyses of the CST was performed using the voxelized tractography as a volumes of interest (Fig 2).

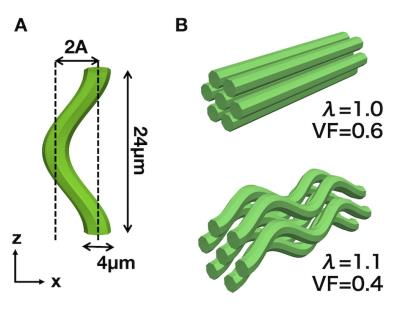
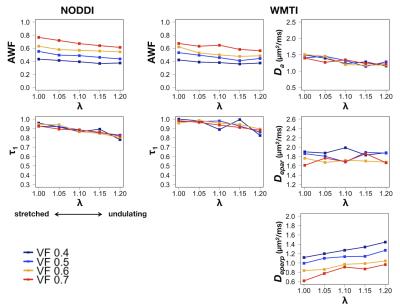
Simulation: Virtual diffusion data were generated using a Monte-Carlo random walk simulation implemented in Camino⁶. We constructed undulating axon cylinder models with radius of 2 µm and wavelength of 24 µm (Fig 3). Strength of undulation is represented by λ (the ratio of the path length in one wave to the wavelength), in accordance with the previous study of undulation⁷. λ equals to 1 in a straight axon, and increases with undulation. The cylinders were hexagonally packed without touching, with varying the occupation within the space (axon volume fraction, VF). Simulations were performed using all combinations of λ = [1, 1.05, 1.1, 1.15, 1.2] and VF = [0.4, 0.5, 0.6, 0.7], and acquisition scheme equivalent to the patient scan.

Results

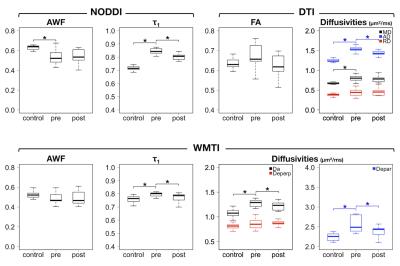
Human data: Significant increase in $$$\tau_{1}$$$ in the iNPH patients was consistently observed for NODDI and WMTI (patients vs controls, 0.84±0.02 vs 0.72±0.04 in NODDI (P<0.001), 0.80±0.02 vs 0.76±0.03 in WMTI (P<0.001)). $$$\tau_{1}$$$ significantly decreased after the surgery (Table 1 and Fig 4). AWF was significantly decreased in the patients in NODDI (0.53±0.07 vs 0.63±0.03 (P=0.002)), though the difference did not reach the significance threshold in WMTI (0.48±0.06 vs 0.53±0.04 (P=0.06)). No significant postoperative changes were observed in AWF. The behaviour of $$$\tau_{1}$$$ and AWF were consistent in NODDI and WMTI, though the estimated values varied between the two.

Simulation: Both NODDI and WMTI showed ability to disentangle the effects from axon stretching and axon density. Especially, it was shown that the effect of VF on $$$\tau_{1}$$$ was very small (Fig 5), suggesting that the changes observed in the patients should be interpreted as a matter of undulation/stretching, and not as a change of axon packing density.

Discussion

Acknowledgements

References

1. Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. NeuroImage 2012;61(4):1000–16.

2. Fieremans E, Jensen JH, Helpern JA. White matter characterization with diffusional kurtosis imaging. NeuroImage 2011;58(1):177–88.

3. Hattori T, Ito K, Aoki S, Yuasa T, Sato R, Ishikawa M, et al. White matter alteration in idiopathic normal pressure hydrocephalus: tract-based spatial statistics study. AJNR Am J Neuroradiol 2012;33(1):97–103.

4. Jurcoane A, Keil F, Szelenyi A, Pfeilschifter W, Singer OC, Hattingen E. Directional diffusion of corticospinal tract supports therapy decisions in idiopathic normal-pressure hydrocephalus. Neuroradiology 2014;56(1):5–13.

5. Jelescu IO, Veraart J, Adisetiyo V, Milla SS, Novikov DS, Fieremans E. One diffusion acquisition and different white matter models: how does microstructure change in human early development based on WMTI and NODDI? NeuroImage 2015;107:242–56.

6. Hall MG, Alexander DC. Convergence and Parameter Choice for Monte-Carlo Simulations of Diffusion MRI. IEEE Transactions on Medical Imaging 2009;28(9):1354–64.

7. Nilsson M, Lätt J, Ståhlberg F, Westen D, Hagslätt H. The importance of axonal undulation in diffusion MR measurements: a Monte Carlo simulation study. NMR Biomed 2011;25(5):795–805.