Introduction

Diffusion-weighted imaging (DWI) has been adopted in many studies of early brain development and neurologic abnormalities in infant brain^1,2, owing to its capability of mapping tissue microstructures and white matter architectures in vivo. However, despite of the advantages of DWI, only few atlases based on diffusion tensor imaging^1,3 and higher angular resolution diffusion imaging^4,5 have been introduced for adult and infant brains. In this abstract, we introduce a longitudinal DWI atlas for the infant brain from birth to one year of age. One novel feature of our method, used to construct the longitudinal atlas from diffusion-weighted images, is that it does not depend on any diffusion models. In addition, our method, based on patch-based sparse representation and motivated from Zhang, et al.⁶, enforces consistency in the spatial and temporal domains on the longitudinal atlas while preserving structural details.

Materials

The atlases were built using the DWI data of 36 infant subjects, scanned at 5 time points (at neonate, 3, 6, 9 and 12 months of age). Using the 3T Siemens Allegra scanner, we acquired 42 diffusion-weighted volumes in non-collinear gradient directions with b = 1000 s/mm² and 7 non-diffusion-weighted volumes for each subject. The image size is 128$$$\times$$$96$$$\times$$$60 with resolution 2$$$\times$$$2$$$\times$$$2 mm³. The images were processed using FSL package⁷ for the correction of eddy current distortion. The brain region was extracted using BET in the FSL, prior to the atlas construction.

Method

Our method consists of two steps: (1) group-wise image normalization and (2) atlas construction using patch-based sparse representation. Specifically, first, the individual images of each time point are aligned to the age-specific common space using linear and then diffeomorphic non-linear transformations via a group-wise registration on their fractional anisotropy (FA) images. The age-specific mean images are further aligned together using the same strategy to a longitudinally common space for all time points. Through this process, we can determine the corresponding patches of all individual images at respective locations at different time points using the estimated transformations. Second, we construct the DWI atlases of each time point using a patch-wise operation determining sparse weights for patches from the individual images. For a patch of the age-specific atlas at a spatial location, we extract its corresponding patches as well as spatio-temporal neighbor patches from the age-specific mean image and the individual images. Here, the patch is defined as a vector of the corresponding voxels of all diffusion-weighted volumes. Also, the spatio-temporal neighbors are determined as patches of corresponding location and their 26-connected neighbors at all time points. The patches from the individual images are atoms of a dictionary ($$$D$$$) for the sparse representation. The patch from the age-specific mean image is used as reference patch ($$$y$$$). Then, multi-task LASSO⁸ can be used to find the optimal sparse weights ($$$x$$$) jointly for the patch and its spatio-temporal neighbors by minimizing the difference between $$$Dx$$$ and $$$y$$$ while enforcing the similarity of the sparse weights across the patch and its spatio-temporal neighbors. Using the sparse weights and patches from the individual images, we determine the voxel intensity of 3$$$\times$$$3$$$\times$$$3 region, surrounding the patch location, for all volumes. It is worth noting that the group sparsity between the patch and its spatio-temporal neighbors, achieved by the multi-task LASSO, helps to transfer both the regional and temporal characteristics of the individual subjects into the atlases.

Results

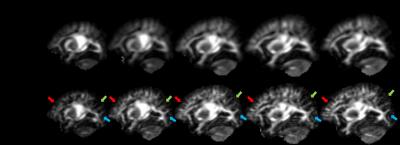
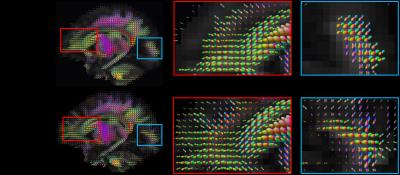
Figure 1 shows the FA images of the group mean atlas and the proposed atlas of each time point. Compared to the group mean atlases, the proposed atlases present more structural details. In addition, the detailed representation of brain structures is consistent across the atlases of all time points. Their changes by time are also found in the proposed atlases (see arrows in Figure 1). These results indicate that our method preserves well the structural details of the individual images across time points. The effectiveness of our method is further supported by Figure 2, which shows the orientation distribution functions (ODFs) of the group mean atlas and the proposed atlas. Unlike the proposed neonatal atlas, many ODFs at cerebral cortex are missing in the group mean atlas.

Conclusion

In this paper, we introduce a method to construct a longitudinal DWI atlas of the infant brain. Our patch-based method results in the atlases with more structural details and greater consistency across time points.

Acknowledgements

This work was supported in part by National Institutes of Health grants (EB008374, MH100217 and NS093842).