Introduction

Arterial spin labelling (ASL) for quantification of tissue perfusion employs magnetically labelled arterial water as an endogenous tracer. Because a diffusible tracer is used, other relevant perfusion-related parameters, such as blood mean transit time and blood volume, are unavailable from an ASL study. Estimation of a tissue impulse response function is further hampered by the rapid decay of the tracer due to the longitudinal relaxation of arterial blood water. However, Kelly et al. (1) investigated ASL-based transit-time parameters, which may serve as useful supplements to CBF information, in an animal study using a 7T small-bore animal MR system and a continuous ASL sequence. In the present study, an improved quantification approach for measuring ASL transit-time parameters is proposed.

Method

The presented methodology is based on a multi-TI ASL measurement, where the dynamics of the inverted spins are described by a Fokker-Planck equation in one dimension. The influence of the random forces in the equation is assumed to occur due to pseudo-diffusion in the capillaries and filtration through the blood brain barrier, while influence of the drag force occurs only due to the bulk flow in the arteries with no arterial dispersions. The proposed solution to the Fokker-Planck equation is based on the bolus tracking solution by Kelly et al. (1), but in the present implementation a measured arterial input function (AIF) is used as input function C₀ (cf. Eq. 1). The underlying fitting processes were accomplished by the curve-fitting routine in Mathematica (Wolfram Research Inc.), using a Nelder-Mead algorithm for unconstrained minimization. The AIF was interpolated prior to the fitting process, and the integral was solved by numerical integration. ASL data were acquired in female Wistar rats (220-250 g body weight) using a 9.4T MRI animal scanner (Agilent Inc., Palo Alto, CA, USA). A single-slice flow-sensitive alternating inversion recovery (FAIR) ASL sequence with a three-shot segmented spin-echo EPI readout was implemented. For each dataset, the ASL signal at ten different time points was acquired, starting at inversion time (TI) 300 ms followed by a 300 ms increment between time points. The relative arterial transit time (rATT) and the capillary transit time (CTT) can be extracted by fitting of experimental data to Eq. 1:

Results

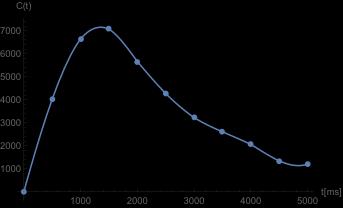
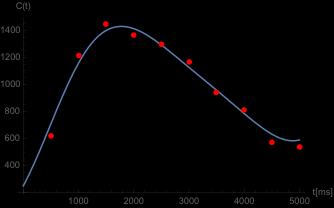
In Figure 1, the measured AIF data points are shown, with the corresponding interpolation superimposed. Figure 2 shows experimental c(t) data for the motor cortex ROI in one animal, together with the resulting model fit.

Conclusions

By using the proposed approach, effects of discrepancies in shape between the assumed and the true AIF are minimized, because the initial distribution becomes better known when a measured arterial input function is used rather than an assumed box function. ASL-based transit-time parameters may provide additional diagnostic information, not revealed by CBF measurements alone. For example, the time for the intravascular water to distribute from arteries through the capillary bed and into the parenchyma can be related to capillary function as well as to the integrity of the blood brain barrier.

Acknowledgements

Lund University Bioimaging Center (LBIC), Lund University, is gratefully acknowledged for providing experimental resources.

References

(1) Kelly ME et al., Phys. Med. Biol. 54 (2009) 1235-1251;