2061

Development of a lesion-wise metric for evaluation of predictive models of prostate cancer on multiparametric MRI

Ethan Leng¹, Jin Jin², Lin Zhang², Joseph S. Koopmeiners², and Gregory J. Metzger¹

¹Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, ²Division of Biostatistics, School of Public Health, University of Minnesota, Minneapolis, MN

Synopsis

A novel lesion-wise metric was developed to evaluate the quality of predictive models of prostate cancer that use quantitative multiparametric MR data to perform prediction on a voxel-wise basis. The metric is based on the Jaccard similarity coefficient and emphasizes overlap and co-localization of ground truth and predicted lesions. Experiments to characterize the metric demonstrated that it qualitatively reflected the goodness of predictions and was more accurate and informative than voxel-wise measures of sensitivity and specificity. We propose that the metric may be customized to select the best predictive models for specific clinical applications such as performing targeted prostate biopsies.

Rationale

Multiparametric MRI (mpMRI) is integral to the clinical management of prostate cancer (PCa),¹ and notably has been used for guiding targeted prostate biopsies.² Recently, there has been interest in developing computational models that use quantitative mpMR data to predict the occurrence of PCa.³ While earlier models were trained using distinct foci of disease (lesions),^3-4 they required the manual identification of ROIs, a process that is inherently subject to interpretation biases. As a result, newer models have favored prediction on a voxel-wise basis.^5-6 However, their performances have thus far only been reported in terms of voxel-wise metrics that may not accurately reflect the ability of the models to correctly identify lesions, which is more relevant clinically. The purpose of this work was to develop a lesion-wise metric that more accurately describes the performance of predictive models.

Methods

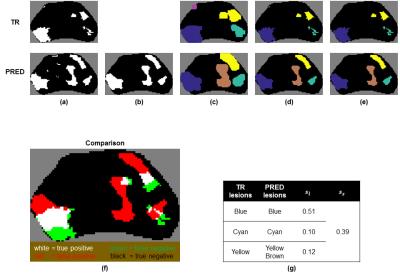
First, cancer voxels in ground truth (TR) and prediction (PRED) maps were grouped into discrete lesions. This was accomplished by performing binary dilation, labeling connected voxels, and then applying the masks of the original maps. For PRED, median filtering was also performed beforehand (Fig. 1a-d). A size threshold to eliminate small lesions was also applied with the rationale that they are likely to represent benign, clinically-insignificant disease (Fig. 1e).⁷

Next, associations between lesions in TR ($$$\ell_{tr}$$$) and lesions in PRED ($$$\ell_p$$$) were determined. For a given $$$\ell_{tr}$$$, an $$$\ell_p$$$ is associated with $$$\ell_{tr}$$$ if they are sufficiently close to each other (e.g., separated by <5 voxels), and is overlapping with $$$\ell_{tr}$$$ if any voxel is labeled cancer in both (Fig. 1f). For each $$$\ell_{tr}$$$, all associated $$$\ell_p$$$s were found with the condition that each $$$\ell_p$$$ is associated with at most one $$$\ell_{tr}$$$. In the case where $$$\ell_p$$$ overlaps with $$$n>1$$$ lesions in TR, $$$\ell_p$$$ is divided into $$$n$$$ lesions such that voxels of partition $$$i$$$ are closest to lesion $$$i$$$ in TR.

After these pre-processing steps, a lesion-wise score $$$s_\ell$$$ was calculated for each $$$\ell_{tr}$$$ (Fig. 1g). $$$s_\ell$$$ was designed to satisfy the following:

1) $$$0 \leq s_\ell \leq 1$$$, with $$$s_\ell=0$$$ when no $$$\ell_p$$$s overlap and $$$s_\ell=1$$$ when $$$\ell_p=\ell_{tr}$$$.

2) $$$s_\ell$$$ increases as overlap and co-localization between $$$\ell_{tr}$$$ and associated $$$\ell_p$$$s improve, where co-localization is quantified by $$$d$$$, the distance between their centroids.

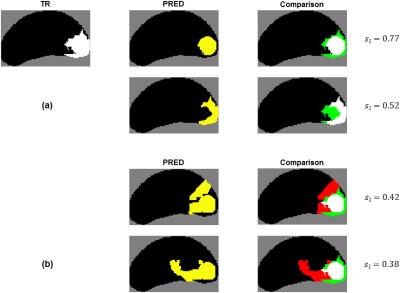
$$$s_\ell$$$ is based on the Jaccard similarity coefficient $$$J_c$$$⁸ (Fig. 2, Eq. 1-2) with two modifications that account for co-localization. The first is a weighting function $$$\omega$$$ (Fig. 2, Eq. 3) that weights the voxels of $$$\ell_{tr}$$$ such that voxels closer to the centroid contribute more heavily to $$$s_\ell$$$ than those at the periphery, which rewards co-localization of TPs (Fig. 3a). The second is a distance penalty function $$$g(d)$$$ that penalizes poor co-localization of both TPs and FPs (Fig. 3b).

$$$s_\ell$$$ may be used in multiple ways. For example, by thresholding $$$s_\ell$$$, the number of lesions detected can be calculated. Additionally, a slice-wise score $$$s_s$$$ can be obtained by averaging all the $$$s_\ell$$$s (Fig. 2, Eq. 4) for a given slice (Fig. 1g).

Results

To characterize the proposed metrics and compare them to voxel-wise metrics, PREDs were synthesized that achieve either target sensitivity and specificity, or target $$$s_l$$$ and/or $$$s_s$$$ on 46 TRs (obtained from our previous work⁶). In the pre-processing step, a size threshold of 50 voxels was applied. For $$$s_\ell$$$, constants $$$a_\omega=1.2$$$, $$$a_1=7$$$, and $$$a_2=1.05$$$ were chosen.

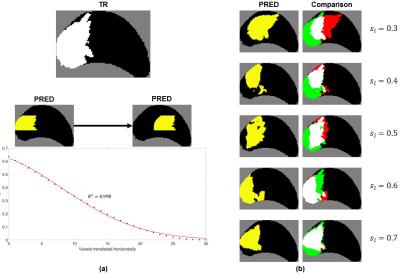
Figure 4a demonstrates how changing the overlap between $$$\ell_{tr}$$$ and $$$\ell_p$$$ affects $$$s_\ell$$$. Figure 4b shows representative PREDs and $$$s_\ell$$$s for a given TR.

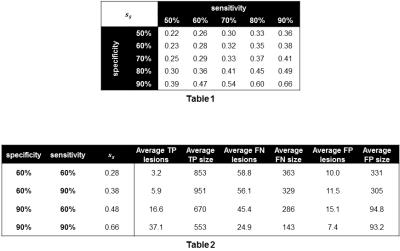
$$$s_s$$$ was calculated over the 46 TRs and averaged across 100 synthetically-generated PREDs for varying voxel-wise sensitivity/specificity pairs (Table 1). Lesion detection statistics were calculated using a threshold of $$$s_\ell=0.5$$$ (Table 2). In general, improvements in specificity increased $$$s_s$$$ more than improvements in sensitivity. This is because there are typically many more non-cancer voxels while $$$s_\ell$$$ and $$$s_s$$$ penalize FNs and FPs equally.

Discussion

As shown in Figures 3 and 4, the proposed metric $$$s_\ell$$$ better reflects the quality of predictions than voxel-wise metrics do. A major task in defining $$$s_\ell$$$ is parameter selection; the parameters were chosen as described above so that qualitatively speaking, $$$s_\ell$$$ would span a wide range of values with $$$s_\ell=0.5$$$ being reasonable threshold for lesion detection. The parameters may also be customized to the specific clinical application of the model. For example, for performing targeted prostate biopsy, co-localization of $$$\ell_{tr}$$$ and associated $$$\ell_p$$$s would be important. $$$\omega$$$ and $$$g(d)$$$ in the calculation for $$$s_\ell$$$ could be tuned accordingly, and the metric could then be used to select the best model for the application.

Acknowledgements

Supported by: NCI R01 CA155268, NIBIB P41 EB015894, DOD/PCRP W81XWH-15-1-0477, MN-REACH.

References

1. Hricak H. MR imaging and MR spectroscopic imaging in the pre-treatment evaluation of prostate cancer. The British journal of radiology. 2005;78 Spec No 2:S103-11. doi: 10.1259/bjr/11253478.

2. Xu S, Kruecker J, Turkbey B, Glossop N, Singh AK, Choyke P, Pinto P, Wood BJ. Real-time MRI-TRUS fusion for guidance of targeted prostate biopsies. Computer aided surgery: official journal of the International Society for Computer Aided Surgery. 2008;13(5):255-64. doi: 10.3109/10929080802364645.

3. Chan I, Wells W, 3rd, Mulkern RV, Haker S, Zhang J, Zou KH, Maier SE, Tempany CM. Detection of prostate cancer by integration of line-scan diffusion, T2-mapping and T2-weighted magnetic resonance imaging; a multichannel statistical classifier. Med Phys. 2003;30(9):2390-8.

4. Vos PC, Hambrock T, Hulsbergen-van de Kaa CA, Futterer JJ, Barentsz JO, Huisman HJ. Computerized analysis of prostate lesions in the peripheral zone using dynamic contrast enhanced MRI. Med Phys. 2008;35(3):888-99.

5. Tiwari P, Kurhanewicz J, Madabhushi A. Multi-kernel graph embedding for detection, Gleason grading of prostate cancer via MRI/MRS. Medical image analysis. 2013;17(2):219-35. doi: 10.1016/j.media.2012.10.004.

6. Metzger GJ, Kalavagunta C, Spilseth B, Bolan PJ, Li X, Hutter D, Nam JW, Johnson AD, Henriksen JC, Moench L, Konety B, Warlick CA, Schmechel SC, Koopmeiners JS. Detection of Prostate Cancer: Quantitative Multiparametric MR Imaging Models Developed Using Registered Correlative Histopathology. Radiology. 2016;279(3):805-16. doi: 10.1148/radiol.2015151089.

7. Rais-Bahrami S, Turkbey B, Rastinehad AR, Walton-Diaz A, Hoang AN, Siddiqui MM, Stamatakis L, Truong H, Nix JW, Vourganti S, Grant KB, Merino MJ, Choyke PL, Pinto PA. Natural history of small index lesions suspicious for prostate cancer on multiparametric MRI: recommendations for interval imaging follow-up. Diagn Interv Radiol. 2014;20(4):293-8. doi: 10.5152/dir.2014.13319.

8. Levandowsky M, Winter D. Distance between Sets. Nature. 1971;234(5323):34-35. doi: 10.1038/234034a0.

Figures

Figure 1. Demonstration of the workflow for generating lesion-wise ($$$s_\ell$$$) and slice-wise ($$$s_s$$$) scores from TRs and PREDs. (a) Original maps: black = non-cancer, white = cancer. (b) Median filtering (3x3) of PRED. (c) Dilation (5x5 square) and color-labeling of connected cancer voxels. (d) Application of masks of original maps. (e) Size-thresholding of small lesions ($$$\leq 50$$$ voxels). (f) Comparison of TR vs. PRED. (g) $$$s_\ell$$$ calculated for each lesion in TR and $$$s_s$$$ calculated for the entire slice.

Figure 2. List and description of the relevant equations.

Figure 3. (a) Two predictions with the same voxel-wise performance (sensitivity = 60%, specificity = 100%). The top prediction is perceived to be better due to superior co-localization of TPs, which is primarily accounted for by the weighting function $$$\omega$$$ and results in a higher score $$$s_\ell$$$. (b) Two predictions with the same voxel-wise performance (sensitivity = 60%, specificity = 90%) and spatial distribution of TPs. The top prediction is perceived to be better due to superior co-localization of FPs, which is accounted for by the distance penalty function $$$g(d)$$$ and results in a higher score $$$s_\ell$$$.

Figure 4. Characterization of $$$s_\ell$$$. (a) Plot of $$$s_\ell$$$ as a given $$$\ell_p$$$ is translated horizontally voxel-by-voxel with respect to a fixed $$$\ell_{tr}$$$. Gaussian curve-fitting demonstrates that $$$s_\ell$$$ decreases exponentially as overlap between $$$\ell_{tr}$$$ and $$$\ell_p$$$ decreases. (b) Representative PREDs for the same TR that achieve scores of $$$s_\ell = 0.3$$$ to $$$s_\ell = 0.7$$$.

Table 1. Characterization of $$$s_s$$$ vs. voxel-wise sensitivity and specificity. $$$s_s$$$ appears to increase linearly with sensitivity and quadratically with specificity. Table 2. Lesion detection statistics for representative voxel-wise sensitivity/specificity pairs shown in Table 1. Associated $$$\ell_p$$$s for a given $$$\ell_{tr}$$$ was defined to be a TP lesion if $$$s_\ell \geq 0.5$$$ and a FN lesion otherwise. Unassociated $$$\ell_p$$$s were defined to be FP lesions. Results were aggregated for the 46 TRs and averaged over the 100 synthetically-generated PREDs.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

2061