2020
Vascular Input Function Correction with Inflow Relative Enhancement Quantification in Liver DCE-MRI1Center for Biomedical Imaging Research, Department of Biomedical Engineering, School of Medicine, Tsinghua University, Beijing, People's Republic of China, 2Clinic for Radiology and Nuclear Medicine, Basel University Hospital, Basel, Switzerland, 3Department of Radiology, University of Wisconsin-Madison, Madison, WI, United States, 4Department of Radiology, University of Washington, Seattle, WA, United States, 5Department of Medical Physics, University of Wisconsin-Madison, Madison, WI, United States, 6Department of Biomedical Engineering, University of Wisconsin-Madison, Madison, WI, United States, 7Department of Medicine, University of Wisconsin-Madison, Madison, WI, United States, 8Department of Emergency Medicine, University of Wisconsin-Madison, Madison, WI, United States
Synopsis
Dynamic contrast enhanced magnetic resonance imaging (DCE-MRI) with pharmacokinetic modeling can help to quantify the perfusion and function of liver. The accurate pharmacokinetic modeling relies on the accurately and reliably captured vascular input function (VIF)s. However, due to the fast blood velocity, the blood in the large vessels including abdominal aorta and the main branch of the portal vein experiences only a limited number of excitations and hasn’t reached a steady state. This introduces bias in the VIFs, and consecutively bias in pharmacokinetic parameters. In this study, we sought to correct the inflow effect on VIF acquisition in liver DCE-MRI.
INTRODUCTION
Dynamic contrast enhanced magnetic resonance imaging (DCE-MRI) with pharmacokinetic modeling can help to quantify the perfusion and function of liver which had been applied in malignancy detection, fibrosis stage classification, cirrhosis estimation (1). The accurate pharmacokinetic modeling relies on the accurately and reliably captured vascular input function (VIF)s. However, due to the fast blood velocity, the blood in the large vessels including abdominal aorta and the main branch of the portal vein (PV) experiences only a limited number of excitations and hasn’t reached a steady state. This introduces bias in the VIFs, and consecutively bias in pharmacokinetic parameters. In this study, we sought to correct the inflow effect on VIF acquisition in liver DCE-MRI.THEORY
Considering that the blood in a small branch of the hepatic vein had reached the steady state $$$M_z^{ss}$$$, the equilibrium magnetization $$$M_z^0$$$ can be calculate use the steady state equation $$$M_z^{ss} = \frac{{M_z^0\left( {1 - {e^{ - TR/{T_1}}}} \right)}}{{1 - cos\alpha {e^{ - TR/{T_1}}}}}$$$ with assumed T1. With regard to the blood in a specified location which had not reached the steady state, equation $$$M_z^{\left( n \right)} = M_z^0\left( {1 - {e^{ - TR/{T_1}}}} \right) + M_z^{\left( {n - 1} \right)}cos\alpha {e^{ - TR/{T_1}}}$$$ (2) can be used to calculate the number of excitations ( $$${N_p}$$$ ) the blood had experienced iteratively until $$$M_z^{\left( {{N_p}} \right)}$$$ is equal to the signal intensity measured on the pre-contrast image. Assuming blood velocity is constant, $$${N_p}$$$ of different dynamic phases can be considered as the same to the pre-contrast phase. Thus, with known $$${N_p}$$$ , the changed T1 of blood after contrast can be calculated more accurately using the same equation. Moreover, the flow in the PV can be estimated, since its direction is nearly perpendicular to the axial plane. Therefore, the SPGR-based flow velocity can be estimated as $$${v_{SPGR}} = \frac{D}{{{N_p}TR}}$$$, where $$$D$$$ is the inflow distance, which can be measured from the images.METHODS
In Vivo Experiment and Image Acquisition
After approval of the institutional animal care and use committee, five pigs were scanned at 3.0T (Discovery MR 750, GE Healthcare, Waukesha, WI). The scan protocol include a respiratory navigator triggered dual-echo DISCO (3) for liver DCE acquisition. The imaging parameters for DISCO sequence were TR/TE1/TE2 = 4/1.5/3ms, FA = 12°, slice thickness = 4 mm, axial plane imaging, in-plane resolution = 1.4 mm. The 2D pencil beam navigator was put on the right liver dome, the acceptance window was set to 30% and temporal resolution was about 7s. After the pre-contrast acquisition, 0.25 mmol/kg of contrast agent (Gd-DTPA) was injected through the marginal ear vein at a rate of 2 mL/s followed by 15 mL 0.9% saline solution flush. Moreover, a respiratory triggered 4D flow (PC-VIPR) sequence (4) was acquired as a reference for blood velocity measurements.
Image Analysis
An ROI was put in the right hepatic vein to measure the $$$M_z^{ss}$$$ of blood for the $$$M_z^0$$$ calculation. The T1 value of blood without contrast was assumed as 1500ms (5). ROIs for the arterial (AIF) and portal venous (PIF) input function extraction were selected and the corresponding contrast concentrations were averaged. $$$R1$$$ of Gd-DTPA at 3 Tesla is 5.14 (/mM/s) (6). For the PV, the $$${v_{SPGR}}$$$ was also calculated. ROIs of liver tissue were selected and fitted using Van Beers model (7) with the corrected and uncorrected AIF & PIF, which were compared using a paired t test. The PC-VIPR images were analyzed, and the main PV was selected to derive the flow velocity, $$${v_{PC}}$$$ . Intra-class correlation (ICC) was used to estimate the consistency between $$${v_{PC}}$$$ and $$${v_{SPGR}}$$$ .
RESULTS
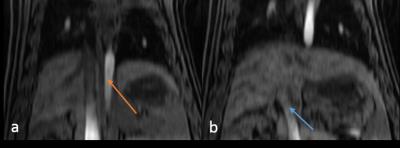
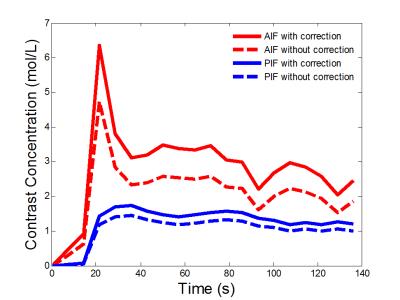
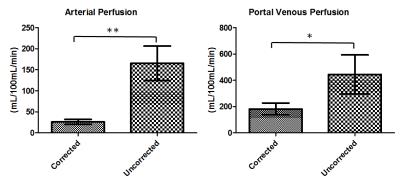
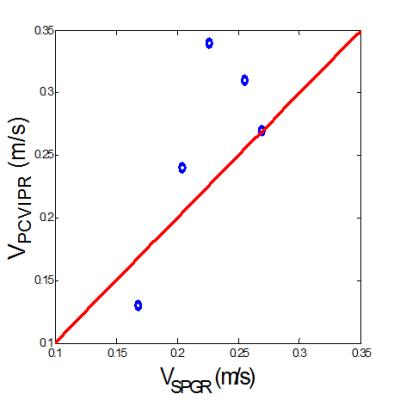
Figure 1 showed a reformatted coronal image of the liver before contrast injection. The obvious signal decrease can be seen along the aorta and PV & superior mesenteric vein from the inflow to the outflow direction, which confirms our theory. One example of AIF and PIF before and after correction is displayed in Figure 2. The amplitude of the corrected AIF and PIF were both higher than the uncorrected. The uncorrected AIF&PIF resulted in significantly overestimated perfusion parameters (P = 0.009 for arterial perfusion and P = 0.033 for portal venous perfusion) (Figure 3). Figure 4 shows the estimated pixel-wise $$${v_{SPGR}}$$$ in PV using the proposed method. Figure 5 shows the scatter plot of $$${v_{PC}}$$$ and $$${v_{SPGR}}$$$ . The ICC between $$${v_{PC}}$$$ and $$${v_{SPGR}}$$$ of PV was 0.856.DISCUSSION
This study could prove that a VIF without inflow correction might lead to significant overestimation of flow parameters. The proposed correction method has the potential to correct the inflow related enhancement effect in liver DCE-MRI analysis, and thus might be able to improve the accuracy of kinetic modeling. The agreement of velocity estimation using the proposed method with PC-MRI further validated the feasibility of the method.Acknowledgements
No acknowledgement found.References
1. Haider MA, Farhadi FA, Milot L. Hepatic Perfusion Imaging: Concepts and Application. Magnetic Resonance Imaging Clinics of North America 2010;18(3):465-475.
2. Liang Z-P, Lauterbur PC. Principles of magnetic resonance imaging: a signal processing perspective: “The” Institute of Electrical and Electronics Engineers Press; 2000.
3. Saranathan M, Rettmann DW, Hargreaves BA, Clarke SE, Vasanawala SS. DIfferential subsampling with cartesian ordering (DISCO): A high spatio-temporal resolution dixon imaging sequence for multiphasic contrast enhanced abdominal imaging. Journal of Magnetic Resonance Imaging 2012;35(6):1484-1492.
4. Frydrychowicz A, Landgraf B, Niespodzany E, Verma R, Roldán-Alzate A, Johnson K, Wieben O, Reeder S. Four-dimensional velocity mapping of the hepatic and splanchnic vasculature with radial sampling at 3 tesla: A feasibility study in portal hypertension. Journal of Magnetic Resonance Imaging 2011;34(3):577-584.
5. Stanisz GJ, Odrobina EE, Pun J, Escaravage M, Graham SJ, Bronskill MJ, Henkelman RM. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magnetic resonance in medicine 2005;54(3):507-512.
6. Sasaki M, Shibata E, Kanbara Y, Ehara S. Enhancement Effects and Relaxivities of Gadolinium-DTPA at 1.5 versus 3 Tesla: A Phantom Study. Magnetic Resonance in Medical Sciences 2005;4(3):145-149.
7. Materne R, Smith A, Peeters F, Dehoux J-P, Keyeux A, Horsmans Y, Van Beers B. Assessment of hepatic perfusion parameters with dynamic MRI. Magnetic resonance in medicine 2002;47(1):135-142.
Figures