1978
Chemical exchange rotation transfer (CERT) using adiabatic hyperbolic secant pulsesEugene C. Lin1, Zhongliang Zu1, Elizabeth A. Louie1, Xiaoyu Jiang1, and Daniel F. Gochberg1
1Vanderbilt University Institute of Imaging Science, Nashville, TN, United States
Synopsis
Chemical exchange rotation transfer (CERT) is an emerging approach for imaging solutes and solute exchange that avoids some of the contributions from the asymmetric background in biological tissues that confound chemical exchange saturation transfer (CEST). To further improve the robustness of CERT methods when there is field inhomogeneity, we examined adiabatic hyperbolic secant pulses for solute saturation. In addition to addressing field homogeneity issues, this new method reveals a new mechanism to generate contrast based on the delay time between pulse.
Purpose
Amide proton transfer (APT) is an important mechanism that may reflect changes in the physiological state. However, most CEST based methods have difficulty quantifying APT due to confounding asymmetric magnetization transfer (MT) and nuclear Overhauser effects (NOE). CERT1 is a pulsed version of CEST that relies on the difference in the water signals when the solutes are rotated by π pulses (labeling scan) and 2π pulses (reference scan). Therefore, homogeneity of B1 is crucial. In order to improve the robustness of CERT and further apply this method to the clinics, we propose a new method (Fig. 1), which replaces Gaussian pulses by adiabatic hyperbolic secant (HS) pulses during the saturation in CERT to obtain accurate rotations.Methods
In order to demonstrate HS-CERT, the three-pool model composed by seven coupled Bloch equations were numerically simulated with the parameters of T1w = 1.5 s, T2w = 60 ms, T1s = 1 s, T2s = 20 ms, T1m = 1 s, T2m = 15 μs, fs = 0.001, fm = 0.1, ksw = 50 Hz, and kmw = 25 Hz, and the lineshape of macromolecule pool is depicted by a super-Lorentzian function. A 50 mM creatine phantom at pH = 6.7 was measured on a 9.4 T Varian small animal scanner at around 23˚C. The HS-CERT metric, named MTRHS, is defined by the difference of the two scans with various pulse train time of repetition (PTR) at the same offset: $$$MTR_{HS}=( S(PTR_{short})-S(PTR_{long}))/S_0$$$. This definition is similar to the metric of conventional CERT, MTRdouble: $$$MTR_{double}=(S(π)-S(2π))/S_0$$$.Results
The three-pool model simulations of the HS-CERT Z-spectrum (Fig. 2A) show that the amount of saturation is related to PTR, likely due to T1 effects during free recovery periods. We choose 200 ms PTR as the reference due to its small effects at the solute resonance, and we examine the effect of varying the PTR of the labeling scan in Fig. 2B. Experimental measurements of creatine using HS-CERT show similar results with long PTR leading to less saturation (Fig. 3A and 3B), and the comparisons with simulations agree with experiments (Fig. 3C). In the extreme cases, such as, 400 or 800 ms PTR, T1 recovery strongly affects the equilibrium during the delays, and raises the baselines indicting that saturation is no longer purely a function of integrated power, which stays constant. These cases are excluded to avoid overestimations of APT. Fig. 3D shows that the contrasts of MTRHS and MTRdouble have comparable contrasts in this particular case. The simulations (Fig. 4) show that the contrasts of MTRHS and MTRdouble have 10% and 25~50% variations, respectively, when B1 has +/- 20% errors. Similarly, the contrasts of MTRHS and MTRdouble have 10% and 20% variations, respectively, when B0 has +/- 100 Hz errors.Discussion
Even though MTRHS and MTRdouble have the same constant integrated power constraint and similar pulse sequences, the MTRHS metric is based on the T1 recovery during the interleaved delays instead of the rotation effect. In this study, we use 200 ms PTR as the reference scan; however, the optimal PTR is still unclear. MTRHS and MTRdouble are based on the assumption that constant integrated power leads to constant baseline saturation, which might not be true when the spins lose the memory due to the long delays. In this preliminary study, the pulse width of HS is 20 ms and β and μ are 529.83 rad/s and 1.78, respectively, which results in the excitation bandwidth of 300 Hz, and these values could be further optimized. Additionally, the pulse width and PTR are independent parameters in the adiabatic condition, which provides another degree of freedom affecting the interactions between pulse and proton exchange of solutes.Conclusion
The preliminary results suggest that the robustness against B1 and B0 inhomogeneity can be improved by implementing adiabatic hyperbolic secant pulses during saturation, which is important to the clinical applications. It also shows that MTRHS has comparable sensitivity to conventional MTRdouble on the creatine phantom. However, the parameter constraints of MTRHS are fundamentally different from those of MTRdouble, and are not yet fully optimized.Acknowledgements
No acknowledgement found.References
1. Zu Z, Xu J, Li H, Chekmenev EY, Quarles CC, Does MD, Gore JC, Gochberg DF. Imaging amide proton transfer and nuclear overhauser enhancement using chemical exchange rotation transfer (CERT). Magn Reson in Med 2014;72(2):471-476.Figures
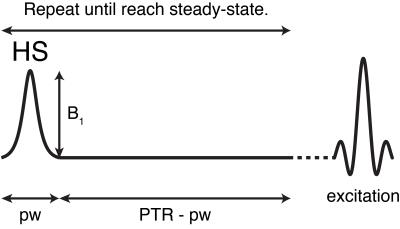
Figure
1. The pulse train in HS-CERT is defined by B1 amplitude (B1),
pulse width (pw) and pulse train time of repetition (PTR).

Figure
2. Three-pool model simulations of HS-CERT. (A) Z-spectrum, the pulse width of
HS is 20 ms, and the average power is 1 μT. (B) The MTRHS obtained from
(A), where the PTRs of labeling scans are 40, 60, 80, and 100 ms, respectively,
and the PTR of reference scan is 200 ms.
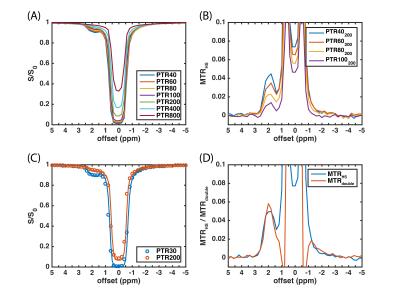
Figure
3. (A) HS-CERT Z-spectrum of the creatine phantom. (B) MTRHS obtained from (A), where
the PTRs of labeling scans are 40, 60, 80, and 100 ms, respectively, and the
PTR of reference scan is 200 ms. (C) The comparison of measurements (circle)
and simulation (line). (D) The comparison of MTRHS and MTRdouble.
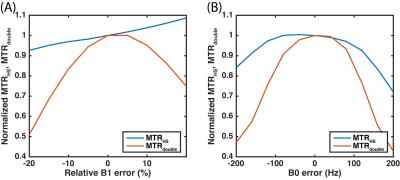
Figure
4. Simulations of relative MTRHS and MTRdouble to B1
(A) and B0 (B) errors.