1967

Enhancing Quantitative Susceptibility Mapping by Using Gradient L2 Regularization with Morphological Priors

Yihao Guo¹, Li Guo¹, Yingjie Mei^1,2, and Yanqiu Feng¹

¹Guangdong Provincial Key Laboratory of Medical Image Processing,School of Biomedical Engineering,Southern Medical University, Guangzhou, People's Republic of China, ²Philips Healthcare, Guangzhou, China.

Synopsis

TKD, LSQR and CSC methods have been proposed to reconstruct QSM from field map. However, these three methods result in inconsistent in the magic angle and can be further improved. This work introduces efficient gradient L2 regularization with morphological information from magnitude images for enhancing the QSM reconstructed by TKD, LSQR and CSC methods.

Purpose

The field to susceptibility source inversion problem is ill-conditioned in quantitative susceptibility mapping (QSM), because the dipole field has values equal or close to zero at the magic angle in the k-space domain. Truncated k-space division (TKD) [1] applies the truncated operator at the magic angle. LSQR [2] and compressed sensing compensated (CSC) inversion [3] exclude the k-space data at the magic angle from the reconstruction of susceptibility maps. A recent study shows that the above three methods can be further improved by enforcing data consistency near the magic angle [4]. In this study, we proposed to enhance QSM by using efficient gradient L2 regularization with morphological information from magnitude images.

Methods

The gradient of truncated k-space division $$$\triangledown \chi_{TKD}$$$ and the morphological priors are combined by L2 regularization and expressed as :

$$$\chi_{p} =argmin\parallel F^{-1}DF\chi-\psi\parallel_2^2+\beta_{1}\parallel M\triangledown\chi\parallel_2^2+\beta_{2}\parallel (1-M)(\triangledown\chi- \triangledown\chi_{TKD})\parallel_2^2 $$$ (1)

Where $$$\chi$$$ is the susceptibility map, $$$ \psi$$$ the tissue field, F the discrete Fourier transform, D the dipole kernel in k-space, $$$\parallel \parallel_2^2$$$ the L2 norm, M the binary mask of smooth regions in the magnitude image, and $$$\beta_{1}$$$ and $$$\beta_{2}$$$ regularization parameters.The second term minimizes the gradient L2 norm of reconstructed susceptibility map in the smooth regions of magnitude image, and thus can effectively suppress streaking artifacts in these regions. The third term imposes the gradient of reconstructed susceptibility map to be close to the gradient of TKD result that contains rapid changing susceptibility details.

The above L2-regularized (L2R) QSM $$$\chi_{p}$$$, which could reserve the energy in the magic angle, can be combined with the various algorithmic QSM $$$\chi_{0}$$$in the k-space [4]:

$$$\chi=F^{-1}[\frac{1}{\alpha+D^{2}} (\alpha F\chi_{p}+D^{2}F\chi_{0})]$$$ (2)

Where $$$\alpha$$$ is a parameter controlling the weights. The flowchart of the proposed method was shown in Fig.1.

To evaluate the performance of L2R method, the numerical simulation, gadolinium phantom and in vivo human brain sets from the online QSM repository [5] were reconstructed by using the TKD, LSQR and CSC methods and then L2R enhancement.

Results

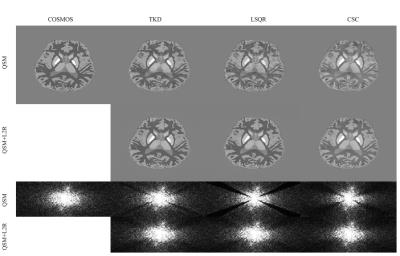
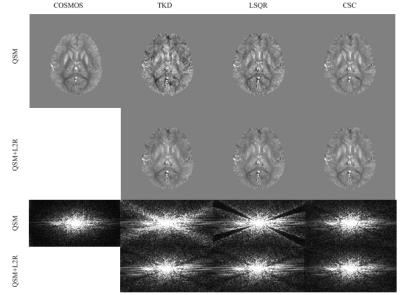
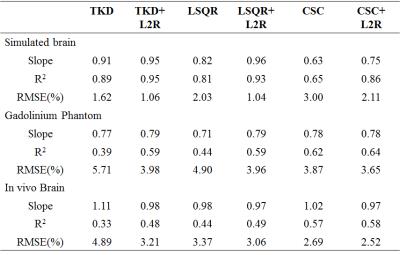
In the numerical simulation, the TKD, LSQR and CSC results (Fig.2) appeared to be noisy in the axial plane, compared with the ground truth. In contrast, the noise was suppressed by L2R enhancement. In the k-space view (Fig.2), there was substantial reduction of signal energy near the magic angle in TKD, LSQR, and CSC results, while the energy was markedly recovered by L2R enhancement. The gadolinium phantom results in Fig. 3 show that the streaking artifacts in the TKD and LSQR reconstructions were markedly suppressed by L2R enhancement. In the k-space view, the signal energy was consistent over the entire k-space. The TKD and LSQR results of the in vivo human brain (Fig.4) appeared to be noisy in the axial plane compared with the COSMOS results, and the noise was effectively suppressed by the proposed method. The signal energy consistency across the k-space was improved by L2R enhancement. Table 1 shows that the proposed method reduced root mean square error (RMSE) and improved determination coefficient (R2) for TKD, LSQR and CSC methods.

Discussion

We developed a novel L2-norm constraint with the gradient of TKD and morphological priors. Although the susceptibility map produced by the TKD method contains severe streaking artifacts, it still reserves some effective gradient information near tissue boundaries. In the proposed method, the gradient of TKD at the edges was effectively employed to enhance the consistency of the k-space and alleviate streaking artifacts. Because the L2 regularization problem has a close form solution, the proposed method is computationally efficient.

Conclusion

The proposed method is efficient and effective for enhancing the consistency of the k-space, suppressing streaking artifacts, reducing RMSE and improving R2 for TKD, LSQR and CSC methods.