1957
Iterative Background Phase Correction: Recovering Data for QSM1Institute of Neuroscience and Medicine - 4, Medical Imaging Physics, Forschungszentrum Jülich, Jülich, Germany, 2Department of Neurology, Faculty of Medicine, JARA, RWTH Aachen University, Aachen, Germany
Synopsis
We present a technique to improve the preparation process of phase data for QSM. In order to compensate for data loss caused by strong local phase gradients near the surface of the brain support, harmonic and dipole-based fitting are used to determine the responsible background fields within an extended brain mask. In an iterative approach, phase data are corrected regarding such contributions prior to further QSM processing steps. This allows for the acquisition of more reliable field maps and larger evaluation masks, which finally leads to more robust susceptibility maps.
Purpose
The
rapidly evolving field of quantitative susceptibility mapping (QSM) enables unprecedented insights into
tissue contrast. Yet, it relies on excellent quality and consistency
of the underlying phase data. Susceptibility contrast between the
brain and its surroundings generates strong local changes of the
static magnetic field, which again cause rapid spatial and temporal
phase evolution and render unwrapping of the phase as well as a
correct estimation of field maps in affected regions impossible.
Common background field removal strategies employed in QSM, such as
PDF1,
SHARP2
or MUBAFIRE3
are not capable of recovering inconsistencies originating in
incorrect field maps. Hence, these areas are commonly excluded in
order to avoid error propagation. Wharton et al. 4
proposed to fit background fields with individually positioned
dipoles. This can be used further to enhance the quality of phase
maps. We present an iterative approach employing harmonic and
dipole-based background field estimation in order to recover phase
data in corrupted regions a
priori, to improve
the mask coverage and to enhance susceptibility mapping robustness.Methods
An in vivo measurement was performed with informed consent on a healthy volunteer at a 3T clinical scanner. For data acquisition, a dual-echo GRE sequence parameterised by: TE=[9.84, 22.14] ms, TR=30ms, α=20°, BW=110 Hz/pixel was used. The first echo of the phase, Φ, is smoothed by a Gaussian of σ=1 voxel to avoid noise propagation. The brain support is segmented with bet25 based on the magnitude. By employing 6-fold (six-neighbour-) dilation an outer confinement mask mmax is created. Based on the local phase coherence6 of the second echo, a more restricted evaluation mask, m, is estimated. The field is calculated from the phase difference between both echo times via Abdul-Rahman unwrapping7. Spherical harmonics and dipole fitting is performed on m within the frame of MUBAFIRE. With the determined coefficients, the corresponding background field bharm is calculated within mmax. The external dipole field bdip is estimated with a Tikhonov approach, using the evaluation mask W=m and the confinement WT=mmax. in: minχ ( || W(blocal – (χext*d)) ||22 + λ||WT χ||22 (see 8) → bdip= χext*d as in 1,8.
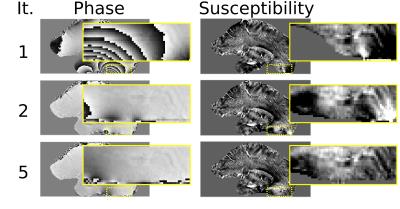
The corresponding background phase is: Φbg=2π·(bharm+bdip)·TE. In the following iteration step, Φbg is subtracted from the measured phase, Φ, and processing is restarted with the calculation of the field map and a new mask as illustrated in Fig. 1. In each iteration, the background-corrected field is estimated by MUBAFIRE and the susceptibility distribution is estimated with a Tikhonov- and gradient-regularised minimisation approach as in 8 (λ=0.03, μ=0.01, 50 it.). The entire process is iterated five times.
Results
The proposed phase correction shows significant improvements in the susceptibility contrast of the sample data within the lower brain regions and close to the brain stem (see Fig. 2) and a reduction in the standard deviation of the background-corrected field (Table 1). Furthermore, the extent of the mask generated by local phase variance estimation can be increased and includes regions that were discarded in the classical approach (corresponds to the first iteration).Discussion
The improved contrast observed in the susceptibility map originates in a better estimation of the field map near the mask edges and in higher mask coverage. Careful optimisation of the presented method regarding automatic phase masking, confinement mask and iteration parameters in the scope of a comprehensive study will further enhance the benefit.Conclusions
We show that our approach improves the evaluation mask, recovers previously unusable phase regions and enhances the quality of the derived susceptibility maps. The presented phase optimisation concept can enable QSM processing of delicate data, subject to strong field distortions or other sources of rapid phase variation e.g. from coil excitation and receive profiles.Acknowledgements
No acknowledgement found.References
1. Liu T, Khalidov I, de Rochefort L, Spincemaille P, Liu J, Tsiouris A J and Wang Y. A novel background field removal method for MRI using projection onto dipole fields (PDF). NMR in Biomedicine. 2011: 24(9), 1129–1136. http://doi.org/10.1002/nbm.1670
2. Schweser F, Deistung A, Lehr B W and Reichenbach J R. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: an approach to in vivo brain iron metabolism? NeuroImage. 2011: 54(4), 2789–807. http://doi.org/10.1016/j.neuroimage.2010.10.070
3. Lindemeyer J, Oros-Peusquens A-M and Shah N J. Multistage Background Field Removal (MUBAFIRE)-Compensating for B0 Distortions at Ultra-High Field. PloS One. 2015: 10(9), e0138325. http://doi.org/10.1371/journal.pone.0138325
4. Wharton S, Schäfer A and Bowtell R. Susceptibility mapping in the human brain using threshold-based k-space division. Magnetic Resonance in Medicine. 2010: 63(5), 1292–304. http://doi.org/10.1002/mrm.22334
5. Smith S M. Fast robust automated brain extraction. Hum. Brain. Mapp.. 2002: 17(3), 143–155. http://doi.org/10.1002/hbm.10062
6. Witoszynskyj S, Rauscher A, Reichenbach J R and Barth M. Phase unwrapping of MR images using Phi UN -- a fast and robust region growing algorithm. Medical Image Analysis. 2009: 13(2), 257–68. http://doi.org/10.1016/j.media.2008.10.004
7. Abdul-Rahman H S, Gdeisat M a, Burton D R, Lalor M J, Lilley F and Moore C J. Fast and robust three-dimensional best path phase unwrapping algorithm. Applied Optics. 2007: 46(26), 6623–35. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/17846656
8. de Rochefort L, Liu T, Kressler B, Liu J, Spincemaille P, Lebon V, … Wang Y. Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: validation and application to brain imaging. Magnetic Resonance in Medicine. 2010: 63(1), 194–206. http://doi.org/10.1002/mrm.22187