Synopsis

Convection-reaction MREPT (crMREPT) method is a more general approach to reconstruct an electrical property map based on B₁-maps from a magnetic resonance imaging (MRI) scanner compared to other existing methods in the literature, such as electrical property tomography (EPT) and local Maxwell tomography (LMT). However, crMREPT shows global spurious oscillations in the reconstructed maps and persistent artifacts in the region when $$$\small\triangledown|B_1|$$$ is small. We propose a solution to effectively mitigate the artifacts by applying a viscosity-type regularization. This abstract shows that the proposed method significantly increases the accuracy of the reconstructed electrical property maps and reduces the sensitivity to noise comparing to crMREPT.

Purpose

Method

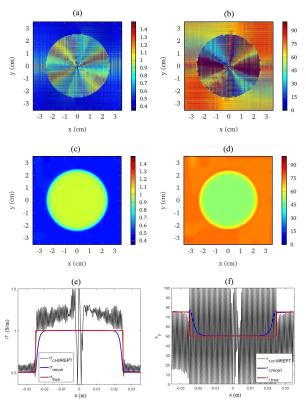
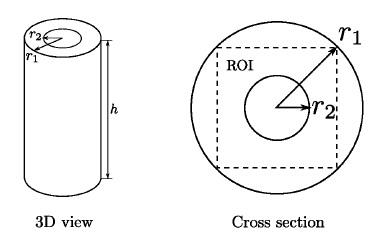
The crMREPT calculates ε and σ by solving the following equation $$$\small\it\left(L+M\right)\cdot\triangledown\gamma-\gamma\triangledown^2H_1^++i\omega\mu H_1^+=0$$$ (1), where $$$\small\gamma=\frac{1}{\sigma+i\omega\epsilon}$$$, $$$\scriptsize H_1^+=\frac{H_x+iH_y}{2}$$$, $$$\scriptsize\it L =\left[-\frac{\partial H_1^+}{\partial x}+i\frac{\partial H_1^+}{\partial y}, -i\frac{\partial H_1^+}{\partial x}-\frac{\partial H_1^+}{\partial y},-\frac{\partial H_1^+}{\partial z}\right]$$$, $$$\scriptsize\it M = \left[-\frac{1}{2}\frac{\partial H_z}{\partial z}, -\frac{i}{2}\frac{\partial H_z}{\partial z}, \frac{i}{2}\frac{\partial H_z}{\partial y}+\frac{1}{2}\frac{\partial H_z}{\partial x}\right]$$$. For a 2D case and when H_z is negligible (e.g. at the center of a birdcage coil) and the spatial variations of H_z are negligible ($$$\small\it M \approx 0$$$), (1) becomes $$$\small\it L_{xy}\cdot\triangledown_{xy}\gamma-\gamma\triangledown^2H_1^++i\omega\mu H_1^+=0$$$ (2), where $$$\scriptsize L_{xy}=\left[-\frac{\partial H_1^+}{\partial x}+i\frac{\partial H_1^+}{\partial y},-i\frac{\partial H_1^+}{\partial x}-\frac{\partial H_1^+}{\partial y}\right]$$$. By applying (2), Fig. 1 (a) and (b) show the reconstructed σ - and ε_r - maps of the region of interest (ROI) of a double-layered cylinder as shown in Fig. 2, respectively. Birdcage coil is used and the working frequency is 128MHz. As shown in Fig. 1 (a) and (b), severe artifacts and oscillations are populated in the maps. Equation (2) is a convection-reaction PDE (crPDE) with complex coefficients. Unlike the crPDE’s with real coefficients, the artifacts of crMREPT cannot be mitigated by increasing the discretization density nor by applying minimization method (avoiding $$$\small\triangledown^2H_1^+\approx0 $$$ or $$$\small H_1^+\approx0$$$). The reason lies in the fact that $$$\small\triangledown^2H_1^+$$$ is not smooth at the boundary where electrical properties are discontinuous in the ROI. Following are the further explanations. If (2) is expressed as $$$\small\overline{F}(\overline{r})\cdot\triangledown_{xy}\gamma=f(\overline{r},\gamma(\overline{r}))$$$ where $$$\small\overline{F}(\overline{r})=\it L_{xy}$$$ and $$$\small f(\overline{r},\gamma(\overline{r}))=\gamma\triangledown^2H_1^+-i\omega\mu H_1^+$$$, the unsmooth $$$\small\triangledown^2H_1^+$$$ in the ROI leads to unanalytic $$$\small f(\overline{r},\gamma(\overline{r}))$$$. According to Cauchy-Kowalevski theorem⁸, unanalytic $$$\small f(\overline{r},\gamma(\overline{r}))$$$ causes unsmooth solutions of (2). To tackle this problem, we propose to apply a viscosity-type regularization⁷ by adding a stabilization term $$$\small\rho\triangledown^2\gamma$$$ to (1) or $$$\small\rho\triangledown_{xy}^2\gamma$$$ to (2) for 2D cases. Equation (2) becomes $$$\small\rho\triangledown^2_{xy}\gamma+\it L_{xy}\cdot\triangledown_{xy}\gamma-\gamma\triangledown^2H_1^++i\omega\mu H_1^+=0$$$ (3)， where $$$\small\rho$$$ is the stabilization constant, $$$\small 0<\rho<1$$$. Finite difference is used for discretization.

Results

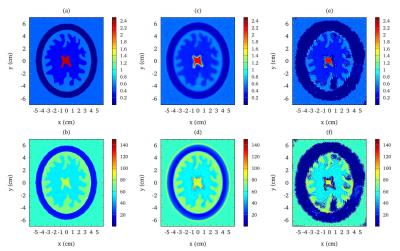
Fig. 1 (c) and (d) show the reconstructed σ - and ε_r - maps of the double-layered cylinder (Fig. 2) by applying the proposed method, respectively. The same coil and frequency are used, $$$\rho$$$ is set to be 0.37. Fig. 1 (e) and (f) show the reconstructed σ and ε_r along y = 0, respectively. Moreover, the data for a simplified human head phantom are used to test the accuracy and noise sensitivity of the method. Fig.3 shows the true maps ((a) (b)), those reconstructed by applying the proposed stabilized crMREPT ((c) (d)), and those by applying crMREPT⁴ ((e) (f)). The noise level (complex white Gaussian noise) is 60 dB.

Discussions

Conclusion

Acknowledgements

References

1. Katscher U, Voigt T, Findeklee C, Vernickel P, et al. Determination of Electric Conductivity and Local SAR Via B1 Mapping. Med. Imaging IEEE Trans. 2009 Sep.28(9):1365–1374.

2. Voigt T, Katscher U, Doessel O. Quantitative conductivity and permittivity imaging of the human brain using electric properties tomography. Magn. Reson. Med. 2011;66(2):456–466.

3. D. K. Sodickson Alon L, Deniz C, et al. Local Maxwell tomography using transmit-receive coil arrays for contact-free mapping of tissue electrical properties and determination of absolute RF phase. ISMRM 2012, 387.

4. Song Y, and Seo J. Conductivity and permittivity image reconstruction at the Larmor frequency using MRI. SIAM J. Appl. Math. 2013; 73(6): 2262-2280.

5. Ammari H, Kwon H, Lee Y, et al. Magnetic resonance-based reconstruction method of conductivity and permittivity distributions at the Larmor frequency. Inverse Problems 2015; 31(10): 105001-105024.

6. Hafalir F, Oran O, Gurler N, et al. Convection-reaction equation based magnetic resonance electrical properties tomography (cr-MREPT). IEEE Trans. Med. Imag. 2014; 33(3): 777-793.

7. Ammari H, Grasland-Mongrain P, Millien P, et al. A mathematical and numerical framework for ultrasonically-induced lorentz force electrical impedance tomography. Journal de Mathmatiques Pures et Appliques 2015; 103(6): 1390 - 1409.

8. Kowalevsky S. Zur theorie der partiellen differentialgleichung. J. Reine Angew. Math. 1875; 80: 1-32.