1915
Absolute Quantification of Brain Perfusion using Golden Angle Compressed Sensing DCE-MRI1Institute of Scientific Instruments of the CAS, Brno, Czech Republic, 2Department of Telecommunications, Brno University of Technology, Brno, Czech Republic
Synopsis
A DCE-MRI method for absolute quantification of cerebral blood flow (CBF) and volume (CBV) and vessel permeability surface area product is presented. It is based on L+S compressed sensing, the two-compartment exchange model (2CXM) and blind deconvolution estimation of the arterial input function. The method is evaluated on data from a healthy rat.
PURPOSE
In brain perfusion imaging, cerebral blood flow (CBF) and volume (CBV) are usually estimated using DSC-MRI. However, DCE-MRI does not provide absolute quantification because of tissue dependent r2 and r2* relaxivities and T1 effects in cases of broken blood brain barrier (BBB).
A possible solution might be use of DCE-MRI. It provides absolute perfusion quantification and is typically used for estimation of permeability of leaky capillaries. DCE-MRI measurement of CBV and especially CBF is difficult due to generally lower r1 relaxivity and low blood volume in a normal tissue. However, it has been shown that it is possible to quantify simultaneously CBV, CBF and permeability in normal brain and brain lesions1,2. The main problem of this approach is to acquire DCE-MRI data with a sufficiently high signal to noise ratio (SNR).
In this initial study, a solution based on compressed sensing (CS) is suggested. It is a way to increase the spatial/temporal resolution and the SNR.
METHODS
Golden angle radial sampling acquisition3 is used (so far as a 2D acquisition method) because it provides a fairly uniform coverage of the k-space with high temporal incoherence for any arbitrary number of consecutive projections. Hence, the temporal sampling rate can be chosen after data acquisition by selecting the number of consecutive projections per image sequence frame.
Furthermore, surface array coil is used for acquisition to include the parallel imaging prior information in the compressed sensing reconstruction. The coil element sensitivities are estimated using the ESPIRiT algorithm4 from separate calibration scans.
The spatio-temporal matrix of the measured image sequence is assumed to be a sum of two components: L with low-rank and S with a sparse gradient along the temporal dimension5. Image sequence reconstruction is then performed by solving an optimization problem consisting of a data fidelity term and two regularization terms promoting the L+S model. The solution is found using the proximal gradient algorithm6.
The reconstructed image sequence is then converted to a sequence proportional to the contrast agent (CA) concentration7. The arterial input function (AIF) is estimated using blind multichannel deconvolution8 from tissue concentration curves extracted from manually drawn brain regions and assuming an intact BBB and the 2CXM pharmacokinetic model9. Finally, voxel-by-voxel perfusion analysis using the 2CXM model results in perfusion parameter maps.
The gradient echo golden angle acquisition method was implemented on a 9.4T BioSpin (Bruker Biospin MRI, Germany) scanner. An experimental dataset was acquired with a normal Sprague-Dawley rat (experiment approved by national authority) using a 4-element surface rat brain array coil and the following parameters: TR/TE 17/1.7ms, flip angle 25deg., axial slice, thickness 2.4mm, acquisition time 14min, contrast agent (Magnevist, Bayer HealthCare Pharmaceuticals, Germany).
First, a “reference” image sequence was reconstructed using 54 projections per frame and the regridding algorithm10. To test the possibility of imaging of several slices (and later extension to a 3D acquisition and image reconstruction), only 21 projections per frame were used further on. This corresponds to the temporal sampling rate Ts=0.357s. Then, every third frame of the reconstructed sequence was used (Ts=1.071s) which leaves time for a theoretical acquisition of two more slices per frame. Furthermore, a TR cycle of 17ms can include excitation and acquisition of approximately 4 slices, hence this experiment simulated acquisition of 12 slices. Two reconstruction algorithms were applied in this scheme: regridding and compressed sensing.
RESULTS
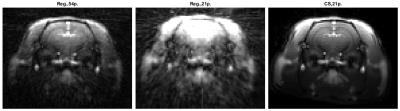
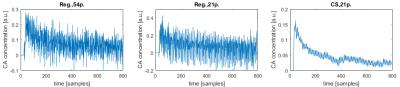
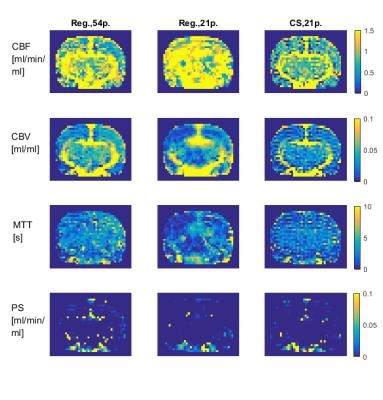
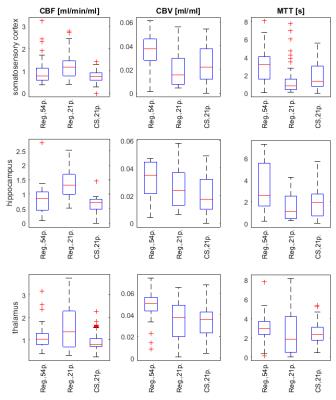
The regridding reconstruction for 54 projections per frame gave a reasonable image quality (Fig.2), fairly noisy tissue concentration curves (Fig.3) and spatially consistent perfusion parameter maps (Fig.4), i.e. increased CBF and CBV in the vascular areas surrounding thalamus, PS close to zero meaning intact BBB. The CBF estimates were in the range of literature values11,12,13 (Fig.5). The CBV was overestimated with respect to literature values 0.01–0.02ml/ml (Fig.5). The regridding reconstruction for 21 projections per frame resulted in severe degradation of images and tissue concentration curves and inconsistent perfusion parameter maps (Figs.2-4) with bias and high variance in the perfusion parameter estimates (Fig.5). The CS reconstruction lead to the best spatial consistency of images and perfusion parameter maps, and a substantial reduction of noise (Figs.2-4). The CBF estimates were in the same correct range as for regridding with 54 projections and CBV was closer to the literature values (Fig.5).DISCUSSION AND CONCLUSION
Golden angle compressed sensing DCE-MRI can be used for absolute quantification of CBF, CBV and PS. It might be especially useful for a better definition of penumbra and for providing additional information on the BBB status. Further extensions to 3D acquisition and reconstruction14 is meaningful and will most probably further improve the results.
Acknowledgements
This work was supported by GACR (1613830S), AZV (16-30299A) and MEYS (LO1212) projects.References
1. Sourbron S, Ingrisch M, Siefert A et al. Quantification of cerebral blood flow, cerebral blood volume, and blood-brain-barrier leakage with DCE-MRI. Magn Reson Med. 2009;62(1):205–217.
2. Ingrisch M, Sourbron S, Morhard D et al. Quantification of Perfusion and Permeability in Multiple Sclerosis. Invest Radiol. 2012;47(4):252–258.
3. Winkelmann S, Schaeffter T, Koehler T et al. An optimal radial profile order based on the golden ratio for time-resolved MRI. IEEE T Med Imag. 2007;26(1):68-76.
4. Uecker M, Lai P, Murphy MJ et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med. 2014;71(3);990–1001.
5. Otazo R, Candès E, Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn Reson Med. 2015;73(3):1125–1136;
6. Combettes PL, Pesquet JC. Proximal splitting methods in signal processing. Fixed- point Algorithms for Inverse Problems in Science and Engineering. 2011;185–212.
7. Schabel MC, Parker DL. Uncertainty and bias in contrast concentration measurements using spoiled gradient echo pulse sequences. Phys Med Biol. 2008;53(9):2345–2373.
8. Jirík R, Soucek K, Mézl M et al. Blind Deconvolution in Dynamic Contrast-Enhanced MRI and Ultrasound. Conf. Proc. IEEE Eng Med Biol Soc. 2014:4276–9.
9. Brix G, Kiessling F, Lucht R et al. Microcirculation and microvasculature in breast tumors: pharmacokinetic analysis of dynamic MR image series. Magn Reson Med. 2004;52(2):420–9.
10. Fessler JA, Sutton BP. Nonuniform Fast Fourier Transforms Using Min-Max Interpolation. IEEE T Signal Proces. 2003;51(2):560–574.
11. Adam J-F, Elleaume H, Le Duc G et al. Absolute cerebral blood volume and blood flow measurements based on synchrotron radiation quantitative computed tomography. J Cereb Blood Flow Metab. 2003;23(4):499–512.
12. Ouchi Y, Tsukada H, Kakiuchi T et al. Changes in cerebral blood flow and postsynaptic muscarinic cholinergic activity in rats with bilateral carotid artery ligation. J Nucl Med. 1998;39(1):198–202.
13. Cremer JE, Seville MP. Regional brain blood flow, blood volume, and haematocrit values in the adult rat. J Cereb Blood Flow Metab. 1983;3(2):254–256.
14. Feng L, Grimm R, Block KT et al. Golden-angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn Reson Med. 2014;72(3):707–717.
Figures