1910

Influence of parameter initial values on DCE parameter estimates in pharmacokinetic modeling: a simulation study
Charlotte Debus1,2,3,4, Ralf Floca5, Amir Abdollahi1,2,3,4, and Michael Ingrisch6

1German Cancer Consortium (DKTK), Heidelberg, Germany, 2Translational Radiation Oncology, Heidelberg Institute of Radiation Oncology (HIRO), German Cancer Research Center (DKFZ), Heidelberg, Germany, 3Department of Radiation Oncology, Heidelberg Ion-Beam Therapy Center (HIT), Heidelberg University Hospital, Heidelberg, Germany, 4National Center for Tumor Diseases (NCT), Heidelberg, Germany, 5Software development for Integrated Diagnostics and Therapy, German Cancer Research Center DKFZ, 6Institute for Clinical Radiology, Ludwig-Maximilians-University Hospital Munich

Synopsis

In pharmacokinetic analysis of DCE-MRI data, the choice of initial parameter values for fitting has been reported to have a significant impact on the outcome of the optimization and hence, on parameter estimates. In this study, we investigated the influence of initial values by fitting simulated concentration time curves with varying combinations of initial parameters, using the two compartment exchange model. The resulting parameter estimates were visualized and compared to the true values, used for simulation, by means of relative errors. Results showed that the choice of initial values has little influence on the precision of the pharmacokinetic analysis.

Purpose

Parameter estimation in dynamic contrast-enhanced MRI is usually performed by fitting a pharmacokinetic model to the measured data, using non-linear least square methods. The two-compartment exchange model (2CXM) describes the compartments „plasma“ and „interstitial volume“ with fractional volumes vp and ve, and their exchange in terms of plasma flow Fp and permeability-surface area product PS1,2. The choice of initial parameter values for fitting can influence the analysis outcome. In the presence of several local minima of the costfunction, the optimizer starting position will determine the direction of search. This effect has been mentioned3 and authors have put forth considerable efforts to compensate it by using time-consuming variations of initial values4. We studied the influence of different starting values on precision and accuracy of parameter estimates in the 2CXM.

Methods

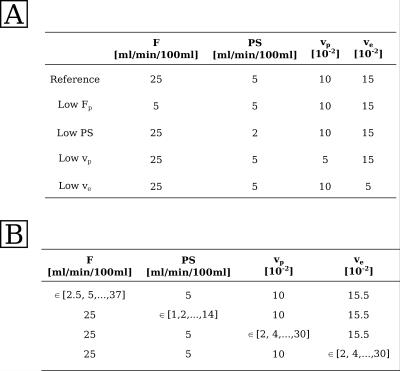
Five types of tissue curves, defined by specific combinations of perfusion parameters (figure 1, table A), were used to simulate time-resolved concentration images of 15x60 px by convolution of a measured arterial input function (temporal resolution 2.11s, 169 timepoints5) with 2CXM tissue response functions. To account for acquisition noise, Gaussian random numbers were added to each data point. Standard deviation of the noise was chosen to achieve a contrast-to-noise ratio (CNR) of 300. CNR is defined as the ratio between AIF peak and standard deviation of the noise.

All curves were fitted with the 2CXM, using an in-house written software module6, implemented in the Medical Imaging Interaction Toolkit7. This tool allows definition of initial optimization values for each parameter on a pixelwise basis, which opens the possibility to use various combinations of initial parameters and graphically visualize the resulting parameter estimates. Parameter constraints were applied to assure model consistency : $$$ 0<v_{p},v_{e}< 1,\: v_{p}+v_{e}<1,\: 0<F_{p}<100\: [ml/min/100ml], \:-1<PS< 100\: [ml/min/100ml] $$$. Initial parameter values were defined in 15x60 px images, with one parameter varying along the x-axis and the other three kept fixed (figure 1, table B). Parameter estimates were averaged over all 60 px with the same set of initial values. Accuracy of the average parameter estimate of all four model parameters $$$\bar{P}_{fit}$$$ was evalutated by means of the relative error with respect to the simulation input values $$$P_{input}$$$: $$E_{rel}= \frac{\bar{P}_{fit} - P_{input}}{P_{input}}$$

Results

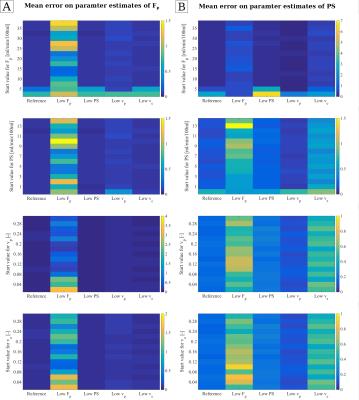
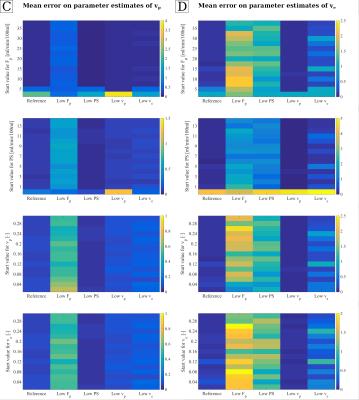
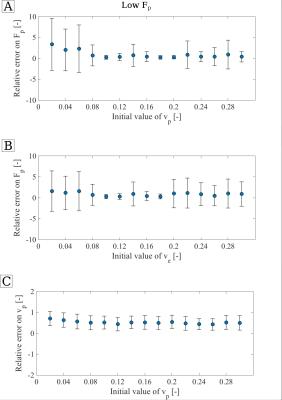
Figure 3 illustrates relative errors on parameter estimates of Fp(A) and PS(B) for the five different curve types (x-axis), fitted with each one parameters' initial value varying as indicated on the y-axis. The errors on parameter estimates on vp(C) and ve(D) are mapped in the same manner in figure 4. Parameter estimates for Fp show low errors, except for low Fp curves. The error is increased in all curve types fitted with low initial values of Fp. For low Fp curves, the estimates on Fp seem to correlate with starting value of vp and ve. For further investigation, the mean errors on Fp is plotted over the initial value of vp and ve in figure 5 A and B. Within the standard deviation, the parameter estimates show no correlation with the initial values. Errors on PS were higher, compared to Fp, and increased for low initial values of Fp and PS. Curves with low Fp or low ve showed higher errors on the estimate for PS. Estimates of vp had low errors, except for curve with low Fp. Errors were increased for inital values Fp=2.5 ml/min/100ml and PS=2.5 ml/min/100ml. For curve types with low Fp, the estimate on vp seems to correlate with the initial value of vp, especially at low starting values. Figure 5C shows the mean error on vp for curves with low plasma flow over the varying initial value of vp. No correlation is visible within the standard deviation. Errors on ve showed the highest errors of all estimates, especially for low Fp and low PS curves. The errors were distinctively larger if the start value for PS was set to 0. Apart from this, no correlation with the initial parameter values can be seen.

Conclusion

The influence of starting values of the optimization routine on the accuracy of the initial parameters is less than expected. Estimates on Fp and PS are sensitive to their own start values if chosen too low. Apart from that, no further correlation between initial value and error on the estimate could be found. Results indicate that time-consuming searches over the initial parameter grid are not necessary, as the effects succumb those generally occuring in pharmacokinetic modeling. However, we investigated the effects of varying one initial parameter. For further clarification, the next step would be to vary initial values for two parameters simultaneously.

Acknowledgements

No acknowledgement found.

References

1 Sourbron, S. P., and Buckley, D. L. "Tracer kinetic modelling in MRI: estimating perfusion and capillary permeability." Physics in medicine and biology 57.2 (2012): R1.

2 Brix, Gunnar, et al. "Tracer kinetic modelling of tumour angiogenesis based on dynamic contrast-enhanced CT and MRI measurements." European journal of nuclear medicine and molecular imaging 37.1 (2010): 30-51

3 Brix, Gunnar, et al. "Pharmacokinetic analysis of tissue microcirculation using nested models: multimodel inference and parameter identifiability.", Medical Physics 36.7 (2009), 2923–2933

4 Buckley, David L. "Uncertainty in the analysis of tracer kinetics using dynamic contrast-enhanced T1-weighted MRI." Magnetic Resonance in Medicine 47.3 (2002): 601-606.

5 Ingrisch, Michael, et al. "Quantification of perfusion and permeability in multiple sclerosis: dynamic contrast-enhanced MRI in 3D at 3T." Investigative radiology 47.4 (2012): 252-258.

6 Debus, Charlotte et al „Impact of fitting strategy on DCE parameter estimates and performance : a simulation study in image space“, 24rd Annual meeting of the International Society of Magnetic Resonance in Medicine (2016), Vol. 24, International Society of Magnetic Resonance in Medicine (ISMRM)

7 Wolf, Ivo, et al. "The medical imaging interaction toolkit (MITK): a toolkit facilitating the creation of interactive software by extending VTK and ITK." Medical Imaging (2004). International Society for Optics and Photonics.

Figures

A: Parameter combinations used to simulate concentration-time curves. Together with a measured arterial input function, each of the parameter combinations was used to generate a homogeneous 15 × 60 px dynamic image (169 time points, temporal resolution 2.11s). These images were fitted with different combinations of initial values for the four model parameters. Each parameters' initial value was either constant over the whole image or varied between 15 different values, as listed in table B.

The arterial input curve used for simulations and representative simulated concentration- time curves of the homogeneous parameter images for different curve types „Reference“, „Low Fp“, „Low PS“, „Low vp“ and „Low ve“. For illustration, the reference curve shows the simulated curve without noise (black line) in comparison to the used curve with Gaussian random noise (red dots). The AIF was taken from measurements of a double bolus injection in the middle cerebral artery (temporal resolution of 2.11s)

Visualization of mean relative errors on parameter estimates of Fp (A: left column) and PS (B: right column) for different curve types „Reference“, „Low Fp“ , „Low PS“ , „Low vp“ and „Low ve“ (indicated on the x-axis of each plot). Each row of plots shows results from fits with varying initial values of either Fp (top row), PS (2nd row), vp (3rd row) or ve (bottom row), while the other three parameter initial values were kept at a fixed value. The respective initial parameter values are labeled on the y-axis of the plots.

Visualization of mean relative errors on parameter estimates of vp (C: left column) and ve (D: right column) for different curve types „Reference“, „Low Fp“ , „Low PS“ , „Low vp“ and „Low ve“ (indicated on the x-axis of each plot). Each row of plots shows results from fits with varying initial values of either Fp (top row), PS (2nd row), vp (3rd row) or ve (bottom row), while the other three parameter initial values were kept at a fixed value. The respective initial parameter values are labeled on the y-axis of the plots.

Relative errors on parameter estimates of Fp over varying initial values of vp (A) and ve (B) and on parameter estimates of vp (C) over varying initial values of vp (A) for concentration curves with low Fp. The starting value of a single parameter took 15 different values along the x-axis, while the other starting values were kept at a fixed value. Parameter estimates were averaged over 60 curves and the relative error was calculated with respect to the original parameter value, used for data simulation. The error bars represent the standard deviation of the mean.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
1910