1909
Comparison of (k,t) sampling schemes for DCE MRI pharmacokinetic parameter estimation1Department of Electrical Engineering, University of Southern California, Los Angeles, CA, United States
Synopsis
We demonstrate an approach to evaluate and compare (k,t) sampling patterns for DCE-MRI. We compute Cramér-Rao lower bounds on the variance of pharmacokinetic (PK) parameter estimates, using pathologically- and anatomically-realistic digital reference objects. The framework allows for the optimization of sampling patterns independent of any specific estimator. We apply this framework to a 2D reference object for four sampling patterns: keyhole, TRICKS, lattice, and golden angle sampling. It is shown that TRICKS, lattice, and golden angle sampling enable low variance estimation for low undersampling factors. Out of these, lattice sampling keeps variances lowest with increasing undersampling factors.
Purpose
Dynamic contrast enhanced MRI (DCE-MRI) of the brain provides a powerful tool to non-invasively assess neurovascular parameters, such as permeability of the brain-blood barrier ($$$K^\text{trans}$$$), plasma ($$$v_\text{p}$$$), and interstitial volume ($$$v_\text{e}$$$). In order to become clinically relevant, measurements of such pharmacokinetic (PK) parameters have to be precise and reproducible.1 Precision of PK parameter maps depends highly on the underlying (k,t) sampling pattern. In this work, we objectively compare (k,t) sampling patterns in a framework that works independent of any specific estimator. This makes the approach more computational efficient than Monte-Carlo approaches for non-linear PK models. Specifically, we develop pathologically- and anatomically-realistic digital reference objects, and use Cramér-Rao analysis to determine a lower bound on PK parameter variances. We demonstrate its utility by comparing four commonly used sampling patterns.Methods
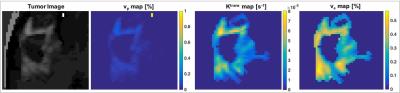
Framework. The Cramér-Rao bound (CRB) gives a lower bound on variances of any unbiased estimator, and has been widely used to optimize MRI experiment design.2,3 Evaluation of the CRB requires the derivatives of the DCE-MRI forward model with respect to the parameters being estimated. The forward model was simulated by PK modeling based on the extended Tofts model, an SPGR sequence, sensitivity encoding, and Fourier undersampling. A population based arterial input function was chosen for this simulation.4 Coil sensitivities for an eight channel head array and noise covariance matrix were taken from measurements. The derivative of the forward model needs to be evaluated at the parameter being estimated. Hence, a pathologically- and anatomically-realistic digital reference object (DRO) 5 was taken to be the ground-truth (Figure 1). CRBs were computed for SNR=20, flip angle of 24°, and 50 time frames at 5s temporal resolution.
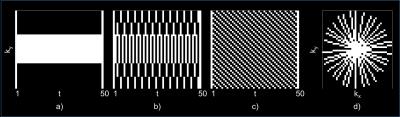
Sampling scheme comparison. Four sampling schemes were compared (Figure 2): keyhole,6 TRICKS,7 lattice,8 and golden angle (GA) sampling.9 CRBs for each sampling pattern with different undersampling factors, i.e., R=2-5,10,15, were examined to determine whether they allow for precise and reproducible parameter estimation (Figure 3,4).
Results
To verify the approach and correctness of the computed CRBs, the results of the framework were confirmed by Monte-Carlo simulations (not shown).$$$$$$
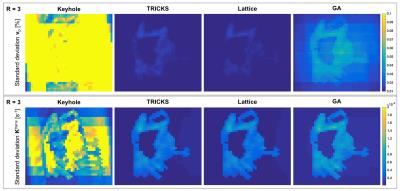
Figure 3 illustrates the spatial pattern of achievable variances for PK parameters $$$K^\text{trans}$$$ and $$$v_\text{p}$$$ across the DRO for R=3. Results for $$$v_\text{e}$$$ are not shown, but are similar. While keyhole sampling leads to high variances across the patch, TRICKS, lattice, and GA sampling show highest variances in the tumor region.
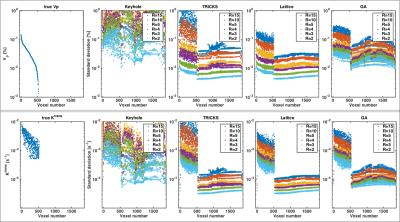
A comparison of best precision achievable with unbiased estimators for varying undersampling factors is shown in Figure 4. Keyhole sampling leads to high variances irrespective the undersampling factor. TRICKS, lattice, and golden angle sampling have reasonably low standard deviation (SD) at low undersampling rates with SDs of less than two percent for $$$v_\text{p}$$$, and one magnitude lower than the $$$K^\text{trans}$$$ to be estimated for R=2,3. As undersampling factors increase, TRICKS sampling shows the strongest rise of bounds, whereas variances for lattice sampling increase most slowly. Nonetheless, SDs are in the same order of magnitude as the parameter to be estimated for R=10,15.
Discussion
The CRB-based approach is computationally efficient, as it does not require expensive Monte-Carlo simulations. Thus, it provides an easier approach to evaluate sampling patterns for DCE-MRI with non-linear PK models. It directly compares the acquired information and allows one to optimize sampling schemes separately from the estimator. Hence, evaluation and optimization of this bound can be seen as a step of providing the most possible information to the estimator. As reconstruction is commonly closely tied to the sampling scheme, the challenge remains to find such unbiased estimator for an optimized pattern.
Despite being faster than Monte-Carlo simulations involving non-linear model fitting, the major challenge of this framework is the rapid increase in computational complexity with matrix size. Let $$$N$$$ be the number of voxels, the Fisher information matrix to be inverted in order to obtain the CRB grows according to $$$(3N)^2$$$. This limits the size of the DRO that can be used for optimization and analysis, but nonetheless allows one to gain insight into properties of sampling patterns.
Conclusion
We demonstrate a framework that allows to compare sampling schemes for DCE-MRI, based on the variance of derived PK parameters. We found that TRICKS, lattice, and golden angle sampling with R=2,3 allow for precise PK parameter estimation in this specific setting. While lowest possible variances rise quickly with increasing undersampling rate, they increase most slowly for lattice sampling for this DRO. Future work needs to investigate the robustness of these results across different DROs and framework settings.Acknowledgements
We thank Ryan Bosca for providing the tumor data and helping to generate the DRO.References
1. B. F. Kurland, E. R. Gerstner, J. M. Mountz, L. H. Schwartz, C. W. Ryan, M. M. Graham, J. M. Buatti, F. M. Fennessy, E. A. Eikman, V. Kumar, K. M. Forster, R. L. Wahl, and F. S. Lieberman, “Promise and pitfalls of quantitative imaging in oncology clinical trials,” Magn. Reson. Imaging, vol. 30, no. 9, pp. 1301–1312, 2012.
2. S. Cavassila, S. Deval, C. Huegen, D. Van Ormondt, and D. Graveron-Demilly, “Cramér-Rao bounds: An evaluation tool for quantitation,” NMR Biomed., vol. 14, no. 4, pp. 278–283, 2001.
3. J. P. Haldar, D. Hernando, and Z. P. Liang, “Super-resolution reconstruction of MR image sequences with contrast modeling,” Proc. IEEE Int. Symp. Biomed. Imaging 2009, no. 1, pp. 266–269.
4. G. J. M. Parker, C. Roberts, A. Macdonald, G. A. Buonaccorsi, S. Cheung, D. L. Buckley, A. Jackson, Y. Watson, K. Davies, and G. C. Jayson, “Experimentally-derived functional form for a population-averaged high-temporal-resolution arterial input function for dynamic contrast-enhanced MRI,” Magn. Reson. Med., vol. 56, no. 5, pp. 993–1000, 2006.
5. R. J. Bosca and E. F. Jackson, “Creating an anthropomorphic digital MR phantom - an extensible tool for comparing and evaluating quantitative imaging algorithms,” Phys. Med. Biol., vol. 61, no. 2, pp. 974–982, 2016.
6. R. A. Jones, O. Haraldseth, T. B. Müller, P. A. Rinck, and A. N. Øksendal, “K-space substitution: A novel dynamic imaging technique,” Mag. Res. Med., vol. 29, no. 6, pp. 830–834, 1993.
7. F. R. Korosec, R. Frayne, T. M. Grist, and C. A. Mistretta, “Time-resolved contrast-enhanced 3D MR angiography,” Magn. Reson. Med., vol. 36, no. 3, pp. 345–351, 1996.
8. P. Kellman, F. H. Epstein, and E. R. McVeigh, “Adaptive sensitivity encoding incorporating temporal filtering (TSENSE),” Magn. Reson. Med., vol. 45, no. 5, pp. 846–852, 2001.
9. S. Winkelmann, T. Schaeffter, T. Koehler, H. Eggers, and O. Doessel, “An optimal radial profile order based on the golden ratio for time-resolved MRI,” IEEE Trans. Med. Imaging, vol. 26, no. 1, pp. 68–76, 2007.
Figures