Synopsis

The reference region model can quantify tumour perfusion without needing an arterial input function (AIF) and provides relative estimates, i.e. K^Trans/K^Trans,RR and v_e/v_e,RR which are usually converted to absolute K^Trans and v_e by using literature-based values for K^Trans,RR and v_e,RR. However, this approach fails to account for inter-patient variability. This study proposes a method that uses the Reference Region and AIF Tail (RRIFT) to estimate patient-specific K^Trans,RR and v_e,RR. The AIF tail is the post-peak part of the AIF and is easier to measure than the complete AIF. Evaluation in simulation and in-vivo showed that RRIFT provides comparable results to Tofts model, and even outperforms the Tofts model at slower temporal resolutions.

Purpose

Tumour perfusion can be quantified by fitting a tracer-kinetic model to Dynamic Contrast Enhanced (DCE) MRI data. Most models require the arterial input function (AIF), i.e. the tracer concentration in an arterial blood vessel. The AIF requires fast temporal resolution to accurately characterize due to its fast peak (1). An alternative is to use reference region methods in which the tracer concentration in a reference tissue serves as a surrogate for the AIF (2). Reference region models provide estimates for the relative transfer constant ($$$K^{Trans}/K^{Trans}_{RR}$$$), relative extravascular extracellular space ($$$v_e/v_{e,RR}$$$), and the rate constant ($$$k_{ep}$$$). For conversion to absolute $$$K^{Trans}$$$ and $$$v_e$$$, literature-based values are typically used for $$$K^{Trans}_{RR}$$$ and $$$v_{e,RR}$$$, but this fails to account for inter-patient variability.

We introduce a method to estimate $$$K^{Trans}_{RR}$$$ and $$$v_{e,RR}$$$ by combining the Reference Region model with the Input Function's Tail (denoted RRIFT). The tail is the post-peak part of the AIF with slow kinetics that can be accurately characterized without high temporal resolution data. An existing similar approach uses the reference region with the AIF tail (3), but requires long acquisition (>20 minutes post-injection), fitting an intermediary model to the reference region data, and is only well-suited for tissues with low $$$K^{Trans}_{RR}$$$

Theory

First, RRIFT takes advantage of the fact that the reference region model directly provides an estimate for $$$k_{ep,RR}$$$ (4). Knowing this, the Tofts model can be re-arranged to estimate $$$K^{Trans}_{RR}$$$ by considering only the tail of the AIF:

$$K^{Trans}_{RR}=\frac{C_{RR}(t)-C_{RR}(t_{tail})+k_{ep,RR}\int_{t_{tail}}^{t}C_{RR}(\tau)d\tau}{\int_{t_{tail}}^{t}C_p(\tau)d\tau}$$

where $$$C_{RR}(t)$$$ is the concentration in the reference region, $$$C_p(t)$$$ is the concentration in blood plasma, $$$t_{tail}$$$ is the start of the AIF tail, and $$$t>t_{tail}$$$. Finally, $$$v_{e,RR}$$$ is obtained using $$$v_{e,RR} = K^{Trans}_{RR} / k_{ep,RR}$$$.

Methods

The feasibility of RRIFT is evaluated in simulation and in-vivo.

Simulated data was generated at a temporal resolution of 1 s with the injection occuring at $$$t=1$$$ min and a total duration of 10 minutes, using a literature-based AIF (2). The reference tissue was defined by $$$K^{Trans}_{RR}=0.1$$$ min$$$^{-1}$$$ and $$$v_{e,RR} = 0.1$$$ while the tissue of interest (TOI) was defined by $$$K^{Trans}_{TOI}=0.25$$$ min$$$^{-1}$$$ and $$$v_{e,TOI} = 0.4$$$. These values represent muscle and tumour, respectively (3). Gaussian noise was added to the TOI curves to produce Concentration-to-Noise Ratios (CNR) (6) ranging from 5 to 50 in 10 equal steps. The data were then downsampled to 5, 10, 15, and 30 s.

The simulation data were processed using the constrained linear reference region model (4) to obtain relative parameters and an estimate for $$$k_{ep,RR}$$$ which was then used with the aforementioned equation to estimate $$$K^{Trans}_{RR}$$$. The AIF tail was defined by $$$t_{tail}=3$$$ minutes, or two minutes post-injection. Next, the estimated $$$K^{Trans}_{RR}$$$ and $$$v_{e,RR}$$$ values were used to convert the relative parameters to absolute parameters, and then their percent errors were calculated.

In-vivo evaluation was performed using DCE-MRI data from five glioblastoma patients in The Cancer Genome Atlas (7), downloaded from the Cancer Imaging Archive (8). The data was acquired using a 3T 3D-SPGR sequence with a temporal resolution of roughly 5 seconds and duration of 6 minutes. The temporalis muscle was used as a reference region. The AIF was approximated by the concentration in the superior sagittal sinus. The complete AIF was used with the Tofts model, while RRIFT only used AIF data acquired after 2 minutes post-injection. Impact of temporal resolution was evaluated by downsampling the data before fitting and then comparing with the high temporal resolution results.

Results and Discussion

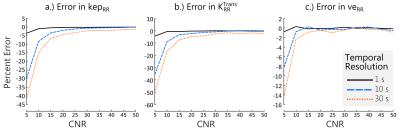
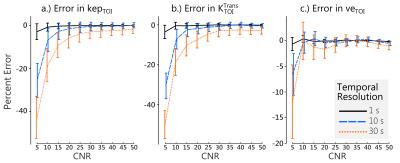
In simulation, RRIFT was able to estimate the reference tissue parameters across a range of noise and temporal resolutions. Errors in $$$K^{Trans}_{RR}$$$ and $$$k_{ep,RR}$$$ were similar (Fig 1a & 1b) while $$$v_{e,RR}$$$ had comparatively smaller errors.The same trend was also seen in the estimates for the tissue of interest (Fig 2).

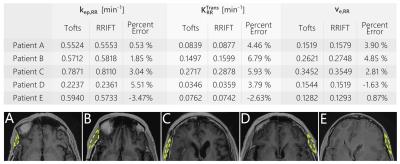
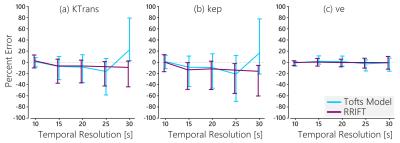
In-vivo, RRIFT provided estimates for the reference tissue that agreed with the Tofts model (Fig 3). RRIFT produced fully quantitative maps similar to the Tofts model at temporal resolutions of 20 s and faster. At slower temporal resolutions, the Tofts model maps for $$$K^{Trans}$$$ and $$$k_{ep}$$$ deviated from the fastest temporal resolution results, while the RRIFT estimates were comparatively stable (Figures 4 & 5). The $$$v_e$$$ estimates were similar for both the Tofts model and RRIFT, and did not experience substantial deviation at slower temporal resolutions.

Conclusion

Acknowledgements

References

1. Henderson E, Rutt BK, Lee T-Y. Temporal sampling requirements for the tracer kinetics modeling of breast disease. Magnetic Resonance Imaging 1998;16:1057–1073. doi: 10.1016/S0730-725X(98)00130-1.

2. Yankeelov TE, Luci JJ, Lepage M, Li R, Debusk L, Lin PC, Price RR, Gore JC. Quantitative pharmacokinetic analysis of DCE-MRI data without an arterial input function: a reference region model. Magnetic resonance imaging 2005;23:519–29. doi: 10.1016/j.mri.2005.02.013.

3. Fan X, Haney CR, Mustafi D, Yang C, Zamora M, Markiewicz EJ, Karczmar GS. Use of a reference tissue and blood vessel to measure the arterial input function in DCEMRI. Magnetic Resonance in Medicine 2010;64:1821–1826. doi: 10.1002/mrm.22551.

4. Ahmed Z, Levesque IR. Increased robustness in reference region model analysis of DCE MRI using two-step constrained approaches. Magnetic Resonance in Medicine 2016. [In Early View] doi: 10.1002/mrm.26530.

5. Parker GJ, Roberts C, Macdonald A, Buonaccorsi G a, Cheung S, Buckley DL, Jackson A, Watson Y, Davies K, Jayson GC. Experimentally-derived functional form for a population-averaged high-temporal-resolution arterial input function for dynamic contrast-enhanced MRI. Magnetic Resonance in Medicine 2006;56:993–1000. doi: 10.1002/mrm.21066.

6. Luypaert R, Sourbron S, Makkat S, Mey J de. Error estimation for perfusion parameters obtained using the two-compartment exchange model in dynamic contrast-enhanced MRI: a simulation study. Physics in Medicine and Biology 2010;55:6431–6443. doi: 10.1088/0031-9155/55/21/006.

7. Scarpace, L., Mikkelsen, T., Cha, soonmee, Rao, S., Tekchandani, S., Gutman, D., … Pierce, L. J. (2016). Radiology Data from The Cancer Genome Atlas Glioblastoma Multiforme [TCGA-GBM] collection. The Cancer Imaging Archive. http://doi.org/10.7937/K9/TCIA.2016.RNYFUYE9

8. Clark K, Vendt B, Smith K, Freymann J, Kirby J, Koppel P, Moore S, Phillips S, Maffitt D, Pringle M, Tarbox L, Prior F. The Cancer Imaging Archive (TCIA): Maintaining and Operating a Public Information Repository, Journal of Digital Imaging, Volume 26, Number 6, December, 2013, pp 1045-1057.