1881
Estimation of Cerebral Blood Flow and Arterial Transit Time Using Partial Volume Corrected Multi-TI Arterial Spin Labeling Imaging1Radiology, Wake Forest School of Medicine, Winston-Salem, NC, United States, 2Biomedical Engineering, Wake Forest School of Medicine, Winston-Salem, NC, United States, 3Clinical and Translational Sciences Institute, Wake Forest School of Medicine, Winston-Salem, NC, United States
Synopsis
A novel PVC algorithm using Multi-TI ASL, acquiring ASL images at multiple PLDs, has been proposed to estimate CBF and ATT in GM and WM separately. A 3D kernel was used to reduce noise sensitivity and improve the estimation power. The proposed method successfully estimated four perfusion parameters (GM CBF, GM ATT, WM CBF, and WM ATT) simultaneously, and may allow region- or voxel-based perfusion analyses in WM, as well as GM.
Introduction
Acquiring ASL images at multiple post-labeling delays (PLD), Multi-TI ASL, has been used to estimate cerebral blood flow (CBF) and arterial transit time (ATT). In simultaneous CBF and ATT estimations, the conventional single tissue model is prone to partial volume effects that reduce detection power and spatial information when smoothed. A kernel-based partial volume correction (PVC) method1 was expanded under the assumption that four perfusion parameters, CBF and ATT in gray matter (GM) and white matter (WM) each, are identical within a kernel.Theory
A kinetic model of continuous or pseudo-continuous labeling2 as a function of the imaging time of slice or volume acquisition, t:
$$ΔM(t)=\begin{cases}2\alpha CBF \cdot M_{0bl}T_{1tiss} e^{-ATT/T_{1bl}} (1-e^{-(t-ATT)/T_{1tiss}}), & ATT+T_{label}>t>ATT\\2\alpha CBF\cdot M_{0bl}T_{1tiss} e^{-ATT/T_{1bl}} (e^{-(t-ATT-T_{label})/T_{1tiss}}-e^{-(t-ATT)/T_{1tiss}}), & t>ATT+T_{label}\end{cases}$$
where ΔM is the perfusion weighted signal, α is the inversion efficiency, M0bl is the equilibrium magnetization of blood, T1tiss is the T1 of tissue, T1bl is the T1 of blood, and Tlabel is the labeling duration.
The conventional CBF and ATT estimation is performed using a single tissue model and its cost function can be expressed as:
$$J(CBF,ATT)= \frac{1}{n}\sum_{i}^n(\Delta M(t_{i})-\Delta M_{meas}(t_i))^2$$
where n is the number of TI, ti is the effective inversion time including the slice delay, ΔMmeas(t) is the measured perfusion-weighted signal.
The cost function of the proposed algorithm includes two tissue types within a kernel:
$$J(CBF_{gm},ATT_{gm},CBF_{wm},ATT_{wm})= \frac{1}{nm}\sum_{j}^m \sum_{i}^n\left\{(f_{gm}\Delta M_{gm}(t_{i,j})+(f_{wm}\Delta M_{wm}(t_{i,j}))-\Delta M_{meas}(t_{i,j}))\right\}^2$$
where m is the number of voxels in the 3D kernel and fgm and fwm are partial volume fractions in GM and WM, respectively.
Methods
Imaging of a single research participant (82 yr old female) was performed on a 3T Siemens Skyra MRI scanner, with a 32-channel head coil (Siemens, Erlangen, Germany). PCASL labeling was used with a labeling duration of 1675ms. Six TIs were used from 1800ms, with increments of 600ms and 8 averages per TI. TR was minimized for each TI. Flow crusher gradients with a cut-off velocity of 5 cm/s were applied in all three orthogonal directions. 2D EPI acquisition with whole brain coverage, matrix size: 64x64x24, 3.4x3.4x5mm voxel size, with 1mm slice gap, 30ms slice delay, GRAPPA with acceleration factor of 2, and scan time of 6:38 (minutes:seconds).
To estimate perfusion parameters on a voxel-wise basis, ASL data were pair-wise subtracted, and then all perfusion-weighted volumes with the same TI were averaged to generate a 6 volume perfusion-weighted time series. T1weighted structural images were skull-striped and segmented into three brain tissues (CSF, GM, WM) using SPM8 to obtain volume fraction maps of GM and WM.
A non-linear constrained optimization method was performed to find per-voxel based perfusion parameters using the cost functions shown above. For the kernel-based PVC, the initial values of four perfusion parameters were first estimated using voxels containing only GM or WM each (fgm or fwm > 0.95) within a larger kernel (i.e. 9x9x3 voxels). The lower bound of CBF was set to zero and that of ATT was set to the shortest post-labeling delay (125ms). The upper bound of CBF was set to 250 and that of ATT set to the second longest TI minus the labeling duration (2525~3215ms). The kernel size of the partial volume correction was 5x5x3 voxels.
To compare with the conventional single tissue model estimation, the perfusion-weighted time series was smoothed with a Gaussian kernel of similar size to the PVC kernel (FWHM of 3x3x1 voxels). The initial values of the estimation were found from the corresponding values at the peak of the time series, and the lower and upper bounds of the optimization was same as the PVC model.
Results
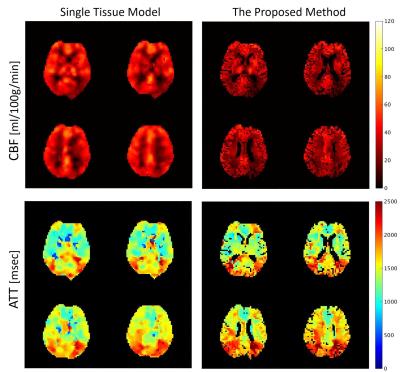
Figure 1 shows four consecutive slices selected from whole-brain coverage maps of CBF and ATT maps in GM and WM. The CBF in WM is substantially lower than in GM, and the occipital lobe shows prolonged ATT both in WM and GM. In addition, the areas close to the main ACA and MCA branches demonstrate short ATT. Figure 2 shows the comparison between the conventional single tissue model and the proposed PVC method. The CBF and ATT maps generally look similar to each other. However, the application of Gaussian smoothing on the single tissue model heavily blurs the CBF and ATT maps, while the proposed method shows excellent distinction of CBF and ATT between GM and WM.Conclusion
This work demonstrates a novel CBF and ATT estimation algorithm using the kernel-based PVC. The method successfully estimated four perfusion parameters simultaneously and allows region- or voxel-based perfusion analyses in WM as well as GM.Acknowledgements
No acknowledgement found.References
1. Asllani I, Borogovac A, Brown TR. Regression algorithm correcting for partial volume effects in arterial spin labeling MRI. Magn Reson Med. 2008;60(6):1362-71.
2. Buxton RB, Frank LR, Wong EC, et al. A general kinetic model for quantitative perfusion imaging with arterial spin labeling. Magn Reson Med 1998;40(3):383-396.
Figures