1872
Diffusion-weighted images super resolution via external and internal patch-based regularization1School of Computer Science, Chengdu University of Information Technology, chengdu, People's Republic of China, 2College of Electronic Engineering, Chengdu University of Information Technology, chengdu, People's Republic of China
Synopsis
Super-resolution (SR) of diffusion weighted imaging (DWI) data is an ill-posed problem, which can be regularized by exploiting diverse priors learned from image patches. In this work, based on patch-based strategy of SR, we propose a new regularization method to reconstruct DW images, which integrates the sparse representation prior with dictionary learned from external image patches and non-local self-similarity prior learned from internal image patches. Meanwhile, in dictionary learning part, nonparametric Bayesian method is adopted to infer dictionary learning variables such as the size of the dictionary from data automatically. Experimental results demonstrate that the proposed method outperforms current methods in DWI reconstruction.
Introduction
High-resolution diffusion weighted imaging (DWI) can benefit the inference for features of the local tissue anatomy and composition1, unfortunately, acquisitions of such data sets are challenging, due to the low signal-noise-ratio (SNR) of DWI. Because of this low-resolution limitation, some methods including super-resolution (SR) techniques initially proposed for natural images have been proposed to tackle with. Recently, many research put more emphasis on patch-based regularization methods, an effective method to solve ill-posed SR problem, which uses prior knowledge to constrain solution space and converts SR problem to the optimization problem 2-6. Patch-based regularization methods for SR problem tend to fall into two categories. Dictionary learning methods learns a sparse basis by exploiting structural similarities on external image patches that are adapted to the image class of interest3,4. However parameters with these non-Bayesian methods such as the dictionary size and the sparsity level have to be set in advance. The empirical settings will result in degraded performance. So the nonparametric Bayesian dictionary learning model is introduced in this abstract that uses the beta process to learn the sparse representation necessary for DW images super resolution. On the contrary, another attempt achieves SR images by exploring self-similarity property among patches in the images5,6. Such an approach considers non-local similarities structural characteristics in image itself and then applies the structural characteristics into image super resolution. In the abstract, we consider a patch-based regularization method that integrates the sparse representation prior with dictionary learned from external image patches and non-local self-similarity prior learned from internal image patches.Methodology
To solve SR problem of DW images with regularization term, the HR image x can be estimated from LR observation y as follows:
\[\hat{\mathbf{x}}={\rm arg} \min\limits_{\mathbf{x}}\; \{||\mathbf{y}-DH\mathbf{x}||+\lambda R(\mathbf{x})\}\]
where \(||\mathbf{y}-DH\mathbf{x}||\) is is fidelity term, \(R(\mathbf{x})\) is the regularization term and \(\lambda\) is the tune parameters to balance them.
A. External patch-based Regularization
One regularizer of our method enforces that patches have a sparse representation according to a dictionary, and corresponding regularization function is
\[R_(x):=\sum_i{\frac{1}{2}||R_i{x}-D\alpha_i||_2^2+\mu||\alpha_i||_1}\]
We consider a Bayesian nonparametric method called beta process factor analysis (BPFA) 3 driven by an underlying Poisson process, than can infer parameters such as the dictionary size and the sparsity level . And we use variational Bayesian inference to update BPFA variables. And then approximately optimize the objective function is:
\[{\rm arg} \min\limits_{\alpha_i}\;{\sum_i{\frac{1}{2}||R_i{x}-D\alpha_i||_2^2}}\]
subject to \(||\alpha_i||_1<=T\quad \forall i\)
B. Internal patch-based regularization
The other regularizer of our method enforces non-local self-similarity approach:
\[R_2(x):=\sum_i{||\sum_j{x_i-w(x_i,x_j)x_j}||^2}\]
Where \(w(x_i,x_j)\) is the weight assigned to \(x_j \) . This weight depends on the similarity between the neighborhood of \(x_i \)and \(\sum_j{w(x_i,x_j)=1}\).
Lastly, we use the alternating direction method of multipliers (ADMM) for optimization.
Result
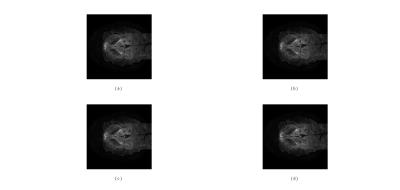
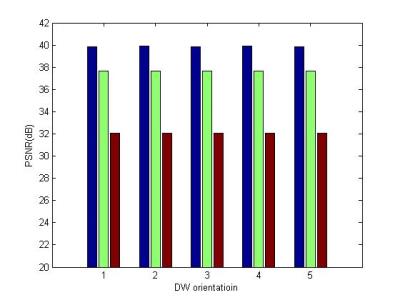
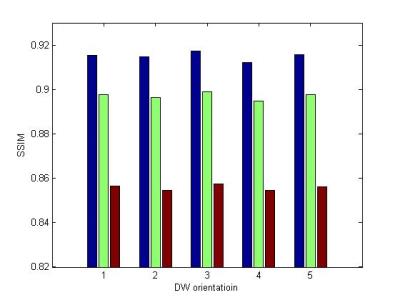
channels. A DW dual spin-echo, SENSE accelerated msh-EPI was used to acquire the DWI data (b-value: 700 s/mm2; 15 diffusion directions); FOV = 210 × 30 × 21 mm3; matrix size = 300 × 300 with 15 slices and a spatial resolution of 0.7 × 0.7 × 2 mm3. To train, the high-resolution DW images in ten diffusion orientation were used for the dictionary construction step. The patch-size and the truncation level in beta process are set to 8 × 8 and 256, respectively. The coupled learned dictionary is shown as Fig.1. To test, the high-resolution DW images in remaining five diffusion orientations were downsampled by a factor of two using the nearest neighbor interpolation along each axis (i.e., [2 2 2]), which resulted in simulated LR images of 1.4 × 1.4 × 4 mm3 as test datasets. Fig.2 presents one slice of a high-resolution DW reconstruction obtained in a specific diffusion orientation, compared with Bicubic interpolated method (Fig.2b), BPFA method (Fig.2c), and the proposed method (Fig.2d). Finally, each reconstruction result is compared with the original high- resolution image using the PSNR and the SSIM showed by Fig.3 and Fig.4, respectively.
Conclusion
The abstract proposed image super-resolution method for DW images with external and internal patch-based regularization instead of with them separately. The sparse prior according to a dictionary learned from external training image patches is considered as external patch-based regularization and the nonlocal self-similarity prior is considered as internal patch-based regularization on image smoothness constraints. We presented an optimization algorithm using the alternating direction method of multipliers (ADMM) and variational Bayesian for updating all BPFA variables. Experimental results on in vivo DW images showed both visual and quantitative results outperform the bicubic interpolation method and BPFA method. In future, for, b0 information will be considered to enhance the DW images super resolution reconstruction resultsAcknowledgements
This work is supported by National Basic Research Program of China (973 Program, No. 2014CB360506), Sichuan Province Science and Technology Support Program (No.2015RZ0008) and Educational Commission of Sichuan Province of China (NO. 15ZA0186)References
[1] Heidi Johansen-Berg and Timothy Behrens. Diffusion MRI, second edition, 2013, Academic Press.
[2] Rousseau F, Kim K, Studholme C. A groupwise super-resolution approach: application to brain MRI [C]. 2010 IEEE International Symposium on Biomedical Imaging: From Nano to Macro. 2010: 860-863.
[3] Huang Y, Paisley J, Lin Q, et al. Bayesian nonparametric dictionary learning for compressed sensing MRI b[J]. IEEE Transactions on Image Processing, 2014, 23(12): 5007-5019.
[4] Polatkan G, Zhou M, Carin L, et al. A bayesian nonparametric approach to image super-resolution[J]. IEEE transactions on pattern analysis and machine intelligence, 2015, 37(2): 346-358.
[5] Manjon J V, Coupe P A, Fonov V, et al. Non-local MRI upsampling.[J]. Medical Image Analysis, 2010, 14(6):784-792.
[6] Coupé P, Manjón J V, Chamberland M, et al. Collaborative patch-based super-resolution for diffusion-weighted images[J]. NeuroImage, 2013, 83: 245-261.
Figures