Synopsis

In this work, we study total-variation (TV) regularization for model-based reconstruction from undersampled DTI data. Various TV regularization methods are examined. Using ex-vivo brain DTI data, we show that imposing TV constraints on DWI provide more reliable quantitative estimates of diffusion than those imposing TV constraints directly on the tensor. A gradient descent algorithm with line backtracking is used for better convergence to optimal solution. For highly undersampled data of 12 diffusion encoding directions and a reduction factor of R=4, we show that good estimates of primary eigen-vector, fractional anisotropy, and mean diffusivity can still be obtained using TV-based regularization.

Introduction

Diffusion tensor imaging (DTI) has provided unprecedent noninvasive visualization of tissue structure such as brain white matter tracts, but its practical applications have been hampered by long scan times and low spatial resolutions. Model-based reconstruction^1,2 combined with sparse sampling and constrained regularization have been used to accelerate DTI. While various methods exist for undersampling in diffusion and/or k-space, the effects of the sparsifying transformation on model-based reconstruction is still not well-understood. In this work, we study the effect of various total variation (TV) regularization on model-based reconstruction from highly under-sampled ex vivo brain DTI data.

Methods

The optimization problem for model-based reconstruction with TV constraints on diffusion weighted image (DWI) can be written¹ as $$$ \text{min}_{\vec{D}} \sum_{n=1}^{N} \parallel \vec F (\vec m_n) - \vec d_n\parallel^2+ \alpha \sum_{n=1}^N \text{TV}(\tilde{m}_n), $$$ where $$$N$$$ is total number of diffusion encoding direction, $$$ \tilde{m}_n=I_0 e^{-b g_n^T \vec D g_n}$$$ is estimated DWI for n-th diffusion encoding direction, $$$ \vec D$$$ is diffusion tensor, $$$ \vec{d}_n$$$ is k-space data, $$$\vec{F} (\vec m_n) $$$ is downsampled Fourier transform of $$$ \tilde{m}_n.$$$ In this work, we consider alternative methods of TV regularization. These include

(1) 3D-TV of DWI:$$$ \small \text{TV}_1 =\sum_{n\in I} \parallel(\tilde{m}_n)_x\!\parallel_1 + \parallel(\tilde{m}_n )_y\parallel_1 + \parallel(\tilde{m}_n)_z\parallel_1,$$$ where $$$ \small (\tilde{m}_n)_x, (\tilde{m}_n)_y, (\tilde{m}_n)_z $$$ denote directional gradients of $$$ \small \tilde{m}_n $$$ with respect to $$$ x, y, z$$$, respectively. The set $$$ I $$$ denotes a set of directions, which can include the set of diffusion encoding directions used in the fidelity term and also additional directions.

(2) TV based on joint sparsity of DWI:$$$ \small \text{TV}_2 = \parallel \sqrt{ \sum_{n\in I} (\tilde{m}_n )^2_x} \parallel_1 +\parallel \sqrt{ \sum_{n\in I} (\tilde{m}_n )^2_y} \parallel_1 + \parallel \sqrt{ \sum_{n\in I} (\tilde{m}_n )^2_z} \parallel_1$$$.

(3) TV of mean diffusivity: $$$ \small \text{TV}_3 = \parallel(\text{Tr}(\vec D))_x\!\parallel_1 + \parallel(\text{Tr}(\vec D))_y\!\parallel_1 + \parallel(\text{Tr}(\vec D))_z\!\parallel_1$$$.

(4) Combinations of TVs: $$$ \small \text{min}_{\vec D}\; {\text{Fid}}/{ \text{Fid}_0} + \alpha_2 {\text{TV}_2}/{\text{TV}_{2,0}} + \alpha_3 {\text{TV}_3}/{\text{TV}_{3,0}}, $$$ where $$$\small \text{Fid}_0,\text{TV}_{i,0}, i=2,3$$$ denote the value of fidelity term and $$$ \small \text{TV}_{i}$$$ for the low-resolution initialization.

Optimization method: We adopt gradient descent with backtracking line search⁴ according to $$$\small \vec p_k=-{\bigtriangledown f(\vec{D_k})}/{ \parallel \bigtriangledown f(\vec{D_k}) \parallel_2}$$$, where $$$f(.)$$$ is the objective function. At each backtracking iteration, the step size scales by half until the Wolfe's Condition$$$ \small f(\vec{D}_k+ \alpha \vec{p}_k) > f(\vec{D}_k) + {\alpha}/{2} \cdot{\bigtriangledown f(\vec{D}_k)}^T \cdot \vec{p}_k$$$ is met.

Results

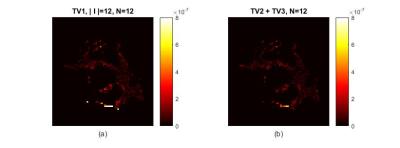
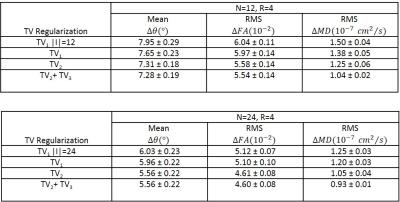
We apply retrospective undersampling to a fully-sampled 3D, Cartesian k-space, DTI spin echo brain dataset consisting of 96 diffusion encoding directions. Diffusion tensor estimates from the fully sampled dataset were used as gold-standard. Four test datasets for $$$N=12 $$$ and four for $$$ N=24$$$ were selected from original dataset and downsampled with reduction factor $$$R=4$$$. we consider four regularization methods: (1) $$$TV_1$$$ with $$$ | I | $$$ equals $$$ N$$$, (2) $$$TV_1$$$ with larger $$$I $$$, (3) $$$TV_2$$$, and (4) combined $$$TV_2+TV_3$$$. For the latter three methods, $$$I$$$ contain all 96 directions. Empirically, we find setting regularization parameters $$$ \alpha_i, i=1,2 $$$ to be 0.4 and $$$ \alpha_3 $$$ to be 0.075 gives best results. Table 1 shows fiber orientation deviation angle error (AE), which is the angle error between estimated primary eigenvector with that of gold-standard, root-mean-square-error of fractional anisotropy (FA) and mean diffusivity (MD). We note that $$$\text{TV}_2 +\text{TV}_3 $$$ provides best estimates among the four methods. Much of the gain comes from imposing the group sparsity constraint instead of the L₁ constraint. The improvement by incorporating $$$\text{TV}_3$$$ is limited. Figure 1 shows the baseline image. Figure 2 and 3 show FA error images and MD error images for methods (1) and (4) above. An FA mask is applied to take into account only voxels with FA values above 0.3^1. Both figures show darker error images of method (4) compared to method (1), which agrees with observations in Table 1.

Discussion

Conclusion

We studied TV regularization for model-based DTI reconstruction and concluded that TV of DWI provides reliable quantitative estimates of diffusion tensor. Future work includes study of constrained reconstruction using higher-order tensor models such as diffusion kurtosis imaging and other regularization methods beyond total-variation.

Acknowledgements

References

1. Welsh CL, DiBella EV, Adluru G, Hsu EW. Model-Based Reconstruction of Undersampled Diffusion Tensor K-Space Data. Magnetic resonance in medicine. 2013;70(2):429-440. doi:10.1002/mrm.24486. 2. Nocedal, Jorge, and Stephen Wright. Numerical optimization. Springer Science & Business Media, 2006. 3. Knoll F, Raya JG, Halloran RO, et al. A model-based reconstruction for undersampled radial spin echo DTI with variational penalties on the diffusion tensor. NMR in biomedicine. 2015;28(3):353-366. doi:10.1002/nbm.3258. 4. Wu, Y., Zhu, Y.-J., Tang, Q.-Y., Zou, C., Liu, W., Dai, R.-B., Liu, X., Wu, E. X., Ying, L. and Liang, D. (2014), Accelerated MR diffusion tensor imaging using distributed compressed sensing. Magn. Reson. Med., 71: 763–772. doi:10.1002/mrm.24721.