Synopsis

Diffusion imaging has proved to be very important in clinical diagnosis and its exclusive application to numerous medical problems is currently plagued with some limitations which is most pronounced in heterogeneous voxels. In order to address this problem, we have presented an analytical method with which diffusion MR signals can be evaluated from point to point within a voxel of interest. The proposed method is shown to be useful in brain tumor diagnosis and general computational tissue imaging. The interesting part of this method is that only few data are required for image reconstruction.

Clinical Question

Impact

Approach

In this innovation, a mathematical formulation of magnetic resonance flow sequence in restricted geometry is developed based on a general second order partial differential equation (Awojoyogbe-Bloch NMR flow equation) [1-3] based on Bessel functions and properties that can make it possible to distinguish cancerous cells from normal cells at the molecular level.

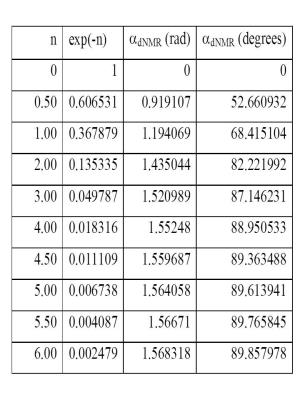
Proposal: The new NMR signal is given by equation (2) and the parameters are defined accordingly in equations (3) and (4). D₀ is apparent diffusion coefficient of the tissue, δ is RF pulse duration, g is gradient magnitude, γ is gyromagnetic ratio while T₁ and T₂ are the tissue relaxation times. If the expressions of equation (5) are true, the general form of the new (proposed) diffusion MRI signal becomes equation (6) for n = 0 and p = -1. Parameter n, is in term of NMR relaxation in the presence of flow and diffusion. We define a very important parameter in diffusion MRI called relaxation angle [1], as defined in equation (7) and presented in Table 1. The choice of angle α_NMR is critical to determine both signal intensity as well as image contrast. The angle α_NMR also depends on the particular pulse sequence utilized. Based on table 1, we can determine which angle α_NMR gives the maximum signal for a given tissue.

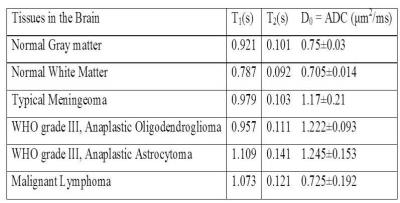
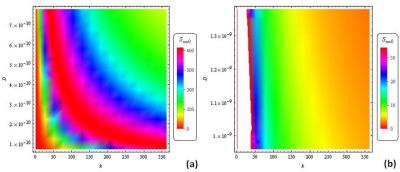
To demonstrate the importance of this proposal, we have applied the algorithm developed to the detection of brain tumors. With the use of a Wolfram Mathematica computer program and the relaxation/diffusion coefficient data in Table 2, we have the profiles in Figure 1 (other profiles are shown in Image 1 of the attached image file). Fast Fourier transform of these profiles are presented in Image 2. Image 3 gives the reconstructed images of the selected tissues via the projection-slice theorem.

Gains and Losses

A new diffusion MRI sequence has been developed based on the fundamental Bloch NMR-Awojoyogbe flow equation with Bessel functions.

Gains

i. For fiber orientation heterogeneity, equations (2-6) are required for the specification of diffusion coefficients as function of space coordinate(s).

ii. Equation (2) satisfies equation (1) in a more comprehensive way where the signal without diffusion S_o, is no longer constant but a Bessel function with MRI parameters.

iii. Parameter S₀ is no longer the signal intensity without diffusion weighting but identifies the measurement's sensitivity to diffusion and can be used to determine the strength and duration of the diffusion gradients.

iv. The MR signal is based on the analytical solution of Bloch NMR flow equation using Bessel functions which is quite easy to build into computer programs.

v. Using a computer program to extract T₁ and T₂ relaxation parameters from MRI clinical examinations by any MRI sequence method, the sensitivity of the MRI system can be explicitly controlled by the order n and u_o. This will greatly change the current practice of diffusion MRI and reduce the number of trial medical examinations thereby minimizing cost.

vi. The Bessel functions can be used for computational diffusion MRI which may be adapted for a particular medical need when sophisticated imaging facilities are unavailable.

vii. Diagnosis/treatment monitoring could be done without the risk associated with health deterioration due to constant administration of therapeutic drugs.

viii. The computer program is able to show impressive contrasts between normal brain tissues and brain tumors.

Losses

i. The program could not show great contrast between different types of brain tumors. Meanwhile, the current images provided may undergo some level of filtering before improved contrasts could be obtained.

Preliminary Data

Acknowledgements

References

[1] Awojoyogbe O. B., Dada O. M., Onwu O. S., Ige A. T., Akinwande I. N. Computational Diffusion MRI Based On Time-Dependent Bloch NMR Flow Equation and Bessel Functions. J. Med. Syst (2016) 40:106 .

[2] Awojoyogbe O.B., Dada O.M., Faromika O.P., Dada O.E (2012): Mathematical Concept of the Bloch Flow Equations for General MRI: A Review; Concepts in Magnetic Resonance Part A, Vol. 38A (3) pp.85–101.

[3] Awojoyogbe, O. B. (2004): Analytical Solution of the Time Dependent Bloch NMR Equations: A Translational Mechanical Approach. Physica A, 339, pp 437-460.

[4] Maier, S.E., Sun, Y. and Mulkern, R.V., 2010. Diffusion imaging of brain tumors. NMR in biomedicine, 23(7), pp.849-864.

[5] Nitz, W.R., Balzer, T., Grosu, D.S. and Allkemper, T., 2010. Principles of MR. In Clinical MR Imaging (pp. 1-105). Springer Berlin Heidelberg.