1846
Diffusion Diffraction Inside Out1Dpt of Radiology, Medical Physics, University Medical Center Freiburg, Freiburg, Germany
Synopsis
Diffusion diffraction, a famous result on NMR in porous media founds little application to in-vivo MRI. Beyond the high technical requirements, the reason can be seen in the principal limitations of this technique. It probes the shape of identical closed pores, which are not typical in-vivo. In this work, we generalize diffusion diffraction for an infinite connected compartment outside impermeable inclusions such as space external to biological cells with low membrane permeability. The signal at high diffusion weighting is expressed in terms of the inclusions' correlation function. The developed theory is supported by experiments in aqueous suspension of polystyrene microbeads.
Purpose
Measurements at ultra-high diffusion weighting is still a `terra incognita' of in-vivo diffusion MRI. The closest result on NMR in porous media is the famous diffusion diffraction$$$^1$$$, which finds little application to biomedical research. The principal limitations of this technique is that it probes the shape of identical closed pores, not really present in biological tissues. In this work, we develop the ideas of diffusion diffraction for an infinite connected compartment outside impermeable inclusions such as space external to biological cells with low membrane permeability. The signal at high diffusion weighting is expressed in terms of the inclusions' correlation function. The developed theory is supported by experiments in aqueous suspension of polystyrene microbeads.Methods
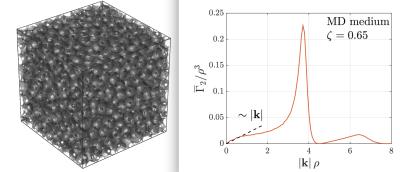
The key point of the method is the realization that the diffusion propagator for long time, $$$t$$$, can be approximated by a Gaussian shape with the excluded volume of inclusions. The latter is taken into account by using the indicator function of inclusions, $$$v(x)$$$, which unity inside and zero outside inclusions. While this function describes the intractably detailed sample structure, a tractable statistical description of the medium is given by the correlation function$$$^2$$$ (Fig.1): $$\Gamma_2(x) = \int\! \frac{d^3x_0}{V} \,v(x_0 + x) \, v(x_0) -\zeta^2 \,, \qquad(1)$$where $$$V$$$ is the sample volume and $$$\zeta$$$ the volume fraction of inclusions (the mean value of $$$v(x)$$$). The measurement is approximated with narrow gradient pulses that evokes encoding with the wave vector $$$q$$$. Simulated medium with a dense packing of identical spheres $$$\zeta \approx 0.65$$$ was generated using event-driven molecular dynamics algorithm$$$^3$$$ with the code downloaded from the authors' website. Experimental samples were prepared by mixing polystyrene microbeads (Microbeads AS, Norway, diameter $$$42.4\,\rm\mu m\pm 2\%$$$ ) with water, centrifuging and squeezing excess water with a microfilter.
Measurements were performed in a 9.4 T BioSpec small animal MR-scanner (Bruker BioSpin MRI, Germany; maximum gradient strength 676 mT/m; 2-channel mouse quadrature volume coil). A 35-direction DWI acquisition (low $$$q$$$, $$$\delta =2.5\,\rm ms$$$, $$$\Delta = 6.25\,\rm ms$$$, $$$T_E= 32\,\rm ms$$$) confirmed that the sample was isotropic. For long diffusion time measurements, PFG were played in the two in-plane directions (x, y). To get close to the narrow pulse approximation, the long time diffusion measurements were run with $$$\delta = 2\,\rm ms$$$ while the $$$\Delta$$$ ranged from 200 to 1000 ms. Measurements parameters were: FOV $$$=$$$ 6 cm, matrix $$$=64 \times 64$$$, slice $$$=6\,\rm mm$$$, $$$T_E = 13\,\rm ms$$$, and maximum q-value $$$= 0.315\,\rm \mu m^{-1}$$$. In a dedicated measurement series, gradient duration $$$\delta$$$ was increased while keeping q the same.
Results
The signal takes the following form in $$$d$$$ spatial dimensions:$$S(t,q) = G_0(t,q) + \frac{1}{(1-\zeta)^2}\int\frac{d^d k}{(2\pi)^d}G_0(t,q-k)\,\Gamma_2(k) \,, \qquad(2)$$where $$$G_0(t,q)=e^{-Dq^2t}$$$ is the Gaussian propagator with the long-time diffusion coefficient $$$D$$$, $$$\Gamma_2(k)$$$ the Fourier-transformed $$$\Gamma_2(x)$$$. For very long diffusion times the Gaussian propagator approaches a scaled delta-function, which results in the signal directly proportional to the medium correlation function. Experimental results are shown in Fig.2 along with the deterministic theoretical prediction (no fitting). Results for increasing $$$\delta$$$ are shown in Fig.3.Discussion
Our results (Fig.2) demonstrate an excellent agreement between the non-fitted theory and the experiment for the diffusion weighting in the y-direction. Agreement for the x-direction is slightly worse with an increased data dispersion. The difference between these measurements could possibly be explained due to some interaction between the diffusion weighting gradient and the stronger readout x-gradient during the EPl. Experimental data confirm the transition from the dominance of the first term in Eq.(2) for small $$$q$$$ to the second term at large $$$q$$$. An underestimation close to the crossover between these regimes can be explained by deviations of the genuine propagator shape from the accepted Gaussian one due to minor violation of the zero-flux boundary condition at the surface of inclusions. Similar experiments were performed by Coy and Gallaghan$$$^4$$$. The difference with the present study was their theory based on the picture of interconnected pores with randomly distributed connection length and orientations. The corresponding parameters were found using a multiparametric fit. In contrast, the present theory relates the signal to the correlation function of the medium, which is the standard statistical description of media with a random component. This description is general, in particular applicable compartments without pronounced `pores' and `connections'. Similarly, inclusions do not need to consist of disconnected particles and can be merged in a diffusion-restricting matrix of any shape with the only limitation that remaining space is connected (for the considered diffusion time). Present results are intended to form a constituent component of future comprehensive theory of diffusion signal at ultra-high diffusion weighting.Acknowledgements
We are grateful to D.S. Novikov for stimulating discussions. This work has been supported by German Research Foundation (DFG), grant KI-1089/3-2.References
[1] P.T. Callaghan, A. Coy, D. Macgowan et al. Diffraction-like effects in NMR diffusion studies of fluids in porous solids. Nature. 1991; 351(6326):467–469.
[2] D.S. Novikov and V.G. Kiselev. Transverse NMR relaxation in magnetically heterogeneous media. J Magn Reson. 2008; 195(1):33–39.
[3] M. Skoge, A. Donev, F.H. Stillinger, S. Torquato. Packing hyperspheres in high- dimensional Euclidean spaces. Phys Rev E. 2006; 74:041127.
[4] A. Coy and, P.T. Callaghan. Pulsed gradient spin-echo NMR ”diffusive diffraction” experiments on water surrounding close-packed polymer spheres. Journal of Colloid and Interface Science. 1994; 168:373–379.
Figures