1834
Comparison of MUSSELS vs MUSE for Multi-Shot Diffusion Imaging1Department of Radiology, University of Iowa, Iowa City, IA, United States, 2Department of Electrical and Computer Engineering, University of Iowa, Iowa City, IA, United States, 3GE Healthcare
Synopsis
Multi-shot diffusion weighted (MS-DW) imaging can offer reduced echo-time (TE) and improved SNR to enable high spatial resolution applications. However, the reconstruction of the high resolution diffusion weighted images (DWI) from the multiple shots is challenging because of the presence of motion-induced phase variations between shots. Recently, two methods were proposed to reconstruct the phase-compensated DWIs. In this work, we compare the performance of the methods, MUSE and MUSSELS, to reconstruct the DWIs from a MS-DW acquisition.
Introduction
Multi-shot diffusion weighted (MS-DW) imaging can offer reduced echo-time (TE) and improved SNR to enable high spatial resolution diffusion imaging applications. However, the reconstruction of the high resolution diffusion weighted images (DWI) from the multiple shots is challenging because of the presence of motion-induced phase variations between the different shots. Recently, two methods were proposed to reconstruct the phase-compensated DWIs. In this work, we compare the performance of the two methods, MUSE1 and MUSSELS2, to reconstruct the DWIs from a MS-DW acquisition.Methods
The MUSE is a phase calibrated method which estimates the motion-induced phase maps for all the shots of a given DWI. The phase calibration relies on a highly regularized reconstruction of the individual shot images. These phase maps are then used to compute the unaliased images from the MS-DW acquisition in a coil sensitivity aided-reconstruction. The MUSSELS method is a phase calibration-less method, which relies on a low-rank property of a structured matrix that is generated from the k-space data of the different shots. The phase-compensated DWI can be recovered by solving a reconstruction problem that uses a SENSE model in addition to the low-rank property.
To compare the methods, diffusion data were collected on a 3T scanner. A 4-shot dual-spin echo diffusion sequence was used with the following parameters: FOV=21cmx21cm, imaging matrix=256x148 with partial Fourier oversampling of 20 lines, slice thickness=4mm. Several experiments were conducted using b-values=700, 1000,1500s/mm2, TE=84-97ms, 15, 30 and 60 diffusion directions, and NEX=2 on two subjects. The coil sensitivity data was computed from the non-diffusion weighted images collected for each acquisition. The data were reconstructed using both methods for the two acquisitions and averaged.
Results
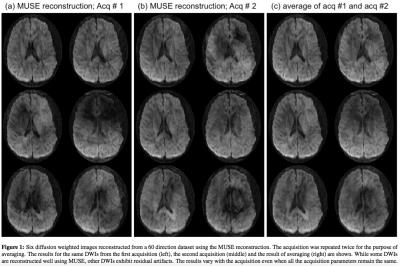
For both the methods, the parameters for the reconstruction were optimized for a few diffusion directions and then kept unchanged for all the other diffusion directions and acquisitions. Figure 1 show the results of MUSE reconstruction. Six DWIs out of the 60 directions are shown that demonstrates the variability in the reconstructions. Since the MUSE reconstruction depends on the phase calibration, the quality of the DWI reconstructed depends upon the accuracy of the phase estimation. It is evident from the results of figure 1 that the phase calibration works well for some diffusion weighted images, but not equally good for all the DWIs. A comparison of the DWIs reconstructed from the two acquisitions show that the results vary with the acquisition as well and that the same parameters may not provide consistent reconstructions for the same acquisition repeated twice. Since the motion itself can be different for the two acquisitions, the above result is not surprising and points to the need that the parameters needs to be tuned for the different acquisitions to reduce the motion-related artifacts.
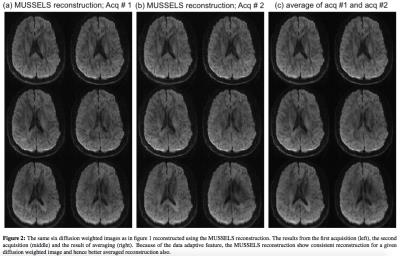
Figure 2 shows the results of the reconstruction using MUSSELS for the same set of DWIs. It is clear from the figure that the MUSSELS reconstruction give much more consistent results for a given DWI across the two acquisitions. Since the MUSSELS reconstruction implicitly corrects for the motion during the structured matrix completion, it can adapt to the data and find data-specific filters that compensates for the phase variations present in the data. As a result, even though the two acquisitions can have different motion, the MUSSELS reconstruction can recover the DWIs reasonably well without the need for tuning. The averaged data computed from both the acquisitions also provide accurate results and provide the SNR boost expected from averaging.
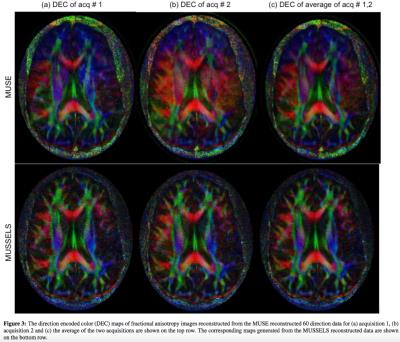
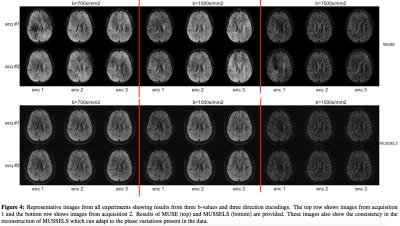
Figure 3 shows the direction encoded fractional anisotropy maps computed for the MUSE and the MUSSELS reconstructions. The inconsistency of the MUSE reconstructions are clearly evident from the direction encoded maps. Representative images from all the experiments for the two reconstructions are shown in figure 4. The same DWI from all the experiments are shown for both the reconstruction methods. These results also make clear that the MUSSELS based reconstruction provide better overall reconstruction for all the direction encodings and b-values tested here.
Conclusion
Our experiments show clear advantage of the calibration-free and data-adaptive nature of the MUSSELS reconstruction. The reconstruction time for MUSE and MUSSELS were 90 & 85 secs respectively per DWI. The MUSSELS method can be further improved to accommodate spatial smoothness into the reconstruction, however, this was not used in the current study. Future studies will compare the reconstruction methods for different spatial resolutions to further characterize the robustness of the two methods.Acknowledgements
No acknowledgement found.References
1. M.-L. Chu, H.-C. Chang, H.-W. Chung, T.-K. Truong, M. R. Bashir, and N.-K. Chen. POCS-based reconstruction of multiplexed sensitivity encoded MRI (POCSMUSE): A general algorithm for reducing motion-related artifacts. Magn Reson Med. , 74(5):1336–48, 2015. ISSN 1522-2594.
2. Mani, M., Jacob, M., Kelley, D. and Magnotta, V. Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magn Reson Med. doi: 10.1002/mrm.26382, 2016
Figures