1827

Estimation of a novel set of intra and extracellular diffusivity parameters from modern DW-MRI
Mario Ocampo-Pineda1, Alessandro Daducci2,3,4, and Alonso Ramirez-Manzanares1

1Computer Science, Centro de Investigacion en Matematicas, Guanajuato, Mexico, 2Computer Science Department, University of Verona, Italy, 3University Hospital Center (CHUV) and University of Lausanne (UNIL), Switzerland, 4Signal Processing Lab (LTS5), École Polytechnique Fédérale de Lausanne, Switzerland

Synopsis

We present a novel framework to estimate on in-vivo data a) independent intra and extracellular axial-diffusivities, b) extracellular radial-diffusivity, c) non-parametric bundle dispersion, d) axonal diameter indexes, and e) intracellular volume fractions. Our methodology does not fix a priori the value of any of these parameters or uses tortuosity models on the extracellular radial diffusivity. The proposal is an extension of the ED^3 method, which provided the best solution on the signal prediction on the White Matter Modelling Challenge 2015. We perform a comprehensive set of synthetic experiments under realistic conditions to validate the capabilities of the proposal.

Introduction and Purpose

Recently, novel acquisition diffusion-weighted (DW) magnetic resonance imaging (MRI) protocols allow to estimate specific white matter microstructure parameters such as axon diameters and intracellular volume fractions (ICVF).1-3 To counter attack the sensibility of the estimators to the signal noise3, some state-of-the-art methods fixed, for instance, the axial diffusivity and use approximated tortuosity models4,5, those strategies stabilize the model fitting but could biased the estimations6,7. Dictionary-based methods have shown an outstanding performance in microstructure estimation at challenging configurations8,9. For instance, the dictionary-based method ED^3 provided the best solution on the signal prediction on the White Matter Modelling Challenge 201510 (cmic.cs.ucl.ac.uk/wmmchallenge), indicating that it can reproduce complex diffusivity profiles and isolate the noisy signals. However such accomplishment does not indicate that the model-parameters are well estimated. In this work: a) we perform an exhaustive study to validate the dictionary-based solver estimation capabilities on modern DW-MRI, and b) we extend ED^3 to estimate a full set of parameters: independent intra and extracellular axial diffusivities, extracellular radial diffusivity, non-parametric dispersion, axonal diameter indexes, and ICVFs. We consider these results are of great importance for the community, because they provide detailed information about the axonal structure on in-vivo data.

Methods

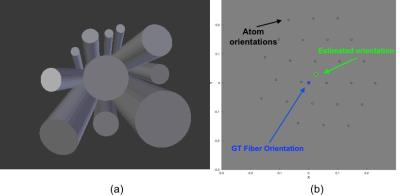
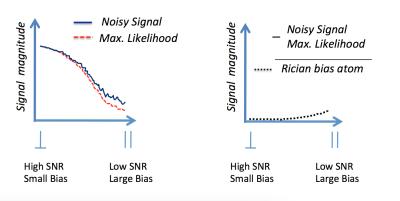
Synthetic Signal Generation: We build a large testing database with realistic synthetic DW-MRI associated with a diverse range of multi-compartment substrates11. We test different intra and extracellular in-vivo Apparent Diffusion Coefficients (ADC) to simulate differences on intra/extracellular viscosity as: $$$ADC_{intra}=1.6\mu m^2/ms$$$ and $$$ADC_{extra}=2.0\mu m^2/ms$$$. Microstructure parameters are varied as follows. ICVF is set in [0.5, 0.7], and axonal radius around [0, 7] $$$\mu m$$$ using approximately 100 radii with gamma distribution. Intracellular signals are generated as in12. By assuming negligible time-dependence (almost all shells have Δ > 20 ms) extracellular signals are generated from the zeppelin model11, where its parameters are estimated from the CAMINO's Monte-Carlo simulator. We introduce dispersion by rotating the intra and extracellular signals with random angles inside a $$$18^\circ$$$ diameter dispersion cone, Figure 1(a). Dictionary settings: Intracellular atoms are generated from the analytical model in12, we use only 3 representative radii {1.41, 3.16, 5.09} $$$\mu m$$$ to capture the size compartments for small [0, 2]$$$\mu m$$$, medium [2, 4] $$$\mu m$$$ and large [4, 6] $$$\mu m$$$ axon radii (these values were optimized experimentally). Axial diffusivity was introduced in the atoms in the range [1.4,2.2]$$$\mu m^2/s$$$. Extracellular atoms for the zeppelin model11 are set with axial and radial diffusivities in ranges [1.4,2.2]$$$\mu m^2/ ms$$$ and [0.4,1.6]$$$\mu m^2/ ms$$$, respectively. Dispersion is modelled in the dictionary by generating oriented intra and extracellular signals along evenly distributed orientations inside a cone of $$$25^\circ$$$ diameter approximately, see Figure 1(b). To reduce the Rician-bias effect13, a novel atom is introduced in the dictionary, it captures the bias magnitude by subtracting the Maximum-Likelihood estimator14 from the noisy signal, this mimics the shape of the bias from perpendicular (high SNR) to parallel acquisitions (low SNR), see Figure 2. We hypothesize this atom could improve the estimation of axial-diffusivities because they depend on MR signals acquired on almost parallel orientations to the axon bundle (on low SNR signals). The combination of the parameters above generates comprehensive dictionaries with approximately 5000 atoms. Optimization: The active atoms are computed by a Non-Negative Linear Least-Squared routine, along with the computation of the average of 100 Bootstrap-Segregation model-fittings to reduce the effect of noise.10

Experiments and results

Acquisition Protocols: The proposal is tested on two MR protocols, the 36-Shell Connectom protocol in15 and the 3-Shell optimized for axonal diameter estimation.3 The SNR for protocol 3-Shell is 35 and for 36-Shell is in range [16,74] for different shells (computed from the S0s available in cmic.cs.ucl.ac.uk/wmmchallenge ). Results: A subset of representative experiments about the quality on the microstructure estimation from data on the 36-Shell and 3-Shell are given in Figure 3 and 4, respectively. The experiments above indicate that the methodology can actually estimate accurately and consistently a full set of useful microstructure parameters from the 36-Shell data. For the 3-Shell protocol the quality degrades, however, the method computes competitive results.

Conclusions and discussion

We proposed a microstructure estimation framework, it does not prefix none of the parameters or uses a priori theoretical tortuosity approximations. A deep synthetic study validates the performance, including tests on two different protocols3,15 under realistic conditions. The experiments indicate a dictionary-based method can predict unseen signals10 and accurately compute useful parameters. The microstructure parameters we estimated on in-vivo experiments15 can be used to validate other methods' performance on clinical settings. Our future work will focus on the optimization of the 36-Shell protocol.

Acknowledgements

M. Ocampo-Pineda was supported by a scholarship from CONACYT, Mexico. A. Ramirez-Manzanares was partially supported by SNI-CONACYT, Mexico, Grants 169338.

References

1. Assaf Y., Blumenfeld-Katzir T., et al. Axcaliber: A method for measuring axon diameter distribution from diffusion MRI. Magnetic Resonance in Medicine. 2008; 59(6): 1347-1354.

2. Zhang H, Hubbard P. L. Axon diameter mapping in the presence of orientation dispersion with diffusion MRI. NeuroImage. 2011; 56:1301–1315.

3. Dyrby T B. and Sogaard L.V., et al. Contrast and stability of the axon diameter index from microstructure imaging with diffusion MRI. Magnetic Resonance in Medicine. 2013; 70(3): 711-721.

4. Alexander D.C., Hubbard P.L., et al. Orientationally invariant indices of axon diameter and density from diffusion MRI. NeuroImage. 2010; 52(4): 1374-1389.

5. Zhang H., Schneider T., et al. NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage. 2012; 61(4): 1000-1016.

6. Jelescu I.O., Veraart J., et al. One diffusion acquisition and different white matter models: How does microstructure change in human early development based on WMTI and NODDI? NeuroImage. 2015;107:242-256.

7. De Santis S., Jones D.K., et al. Including diffusion time dependence in the extra-axonal space improves in vivo estimates of axonal diameter and density in human white matter. NeuroImage. 2016;130:91-103.

8. Daducci A., Canales-Rodríguez E.J., et al. Quantitative Comparison of Reconstruction Methods for Intra-Voxel Fiber Recovery From Diffusion MRI. IEEE Trans. on Med. Imag. 2014;33(2): 384-399.

9. Daducci A., Canales-Rodríguez E.J., et al. Accelerated Microstructure Imaging via Convex Optimization (AMICO) from diffusion MRI data. NeuroImage. 2015; 105: 32-44.

10. Ferizi U., Scherrer B., et al. Diffusion MRI microstructure models with in vivo human brain Connectom data: results from a multi-group comparison. Submitted to NMR in Biomedicine; https://arxiv.org/abs/1604.07287

11. Panagiotaki E., Schneider T., et al. Compartment models of the diffusion MR signal in brain white matter: A taxonomy and comparison. NeuroImage. 2012; 59(3): 224-2254.

12. van Gelderen P., DesPers D., et al. Evaluation of Restricted DIffusion in Cylinders. Phosphocreatine in rabbit leg muscle. Magnetic Resonance. 1994; 103: 255-260.

13. Gudbjartsson H., Patz, S. The rician distribution of noisy MRI data. Magn. Reson. in Med. 1995;34(6): 910-914.

14. Alexander D.C. Modelling, Fitting and Sampling in Diffusion MRI. Springer. Visualization and Processing of Tensor Fields. 2009: 3-20.

15. Ferizi U., Schneider T. A Ranking of Diffusion MRI Compartment Models with In Vivo Human Brain Data. Mag. Reson. in Med. 2014;72:1785-1792.

Figures

Figure 1. (a) Scheme of the arrange used to generate synthetic analytical signals with dispersion. (b) Scheme of the superior view of a set of even base orientations in the half sphere: 25 additional orientations (black circles) with intra/extracellular atoms are introduced in the dictionary to capture dispersion in the substrate around the main fiber orientation (green circle, estimated voxel-wise by DT-MRI). This configuration covers a cone of 25$$$^\circ$$$ diameter approximately. The active atoms in the solution, i.e. with a compartment size value larger than zero, depict the non-parametric shape of the bundle dispersion.

Figure 2. Scheme of the computation of the Rician bias atom introduced in the dictionary: it is computed by smoothing the signal difference between the noisy signal and its Maximun-Likelihood estimator.

Figure 3. Boxplots of the estimated microstructure parameters from 50 model fittings on the Connectom 36-Shell protocol reported in15. Statistical values are shown for different ICVF Ground Truth (GT) configurations in [0.5,0.7]. Results for: (a) estimated ICVFs, (b) volume-weighted axonal-radius indexes, (c) compartment sizes grouped by small ([0,3]$$$\mu m$$$) and large ([3,6]$$$\mu m$$$) axonal radii, and (d) extracellular axial (Ex$$$_\parallel$$$) and radial (Ex$$$_\perp$$$) diffusivities, and intracellular axial diffusivities (In$$$_\parallel$$$). The horizontal green lines indicate the GT values. We note that estimators for small and large compartment sizes in (c) present more accurate results than the volume-weighted axonal-radius indexes in (b).

Figure 3. Boxplots of the estimated microstructure parameters from 50 model fittings on the optimized 3-Shell protocol with SNR=35 as reported in3. Experimental plots are presented in the same grid-configuration as in Figure 3.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
1827