1811
Compact representation of the diffusion signal for multi-shell HARDI1Centre for the Developing Brain, King's College London, London, United Kingdom, 2Division of Imaging Sciences & Biomedical Engineering, King's College London, London, United Kingdom
Synopsis
With the advent of multi-shell acquisition, there is an increasing need for compact linear orthonormal representations of the DWI signal that extend over the radial as well as angular domain. In this work, we evaluate and compare 3 candidate basis function sets: spherical Bessel functions with and without reparametrization and the SHORE basis. Results show that the reparametrized Bessel functions and SHORE basis can faithfully represent the DWI signal with low numbers of parameters, and can be tuned to the properties of the signal independently of acquisition parameters.
Introduction
To date, most diffusion-weighted imaging (DWI) data have been acquired with dense sampling at a single fixed b-value to maximise angular contrast1, and can be efficiently represented using the spherical harmonic basis2. Recent developments in microstructural modelling and multi-tissue decomposition have sparked renewed attention in the radial b-value dependence of the signal. There is therefore a need for a compact linear orthonormal representation of the DWI signal that extends over the radial as well as angular domain. This would be particularly useful for motion and distortion correction, super-resolution image reconstruction, and microstructure modelling.Methods
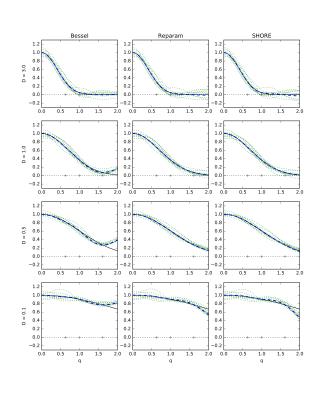
Ideally, basis functions should be orthonormal and separable in spherical coordinates, i.e., $$$\Phi_{nlm}(q,\theta,\phi) = R_n(q) Y_l^m(\theta,\phi)$$$ with $$$Y_l^m$$$ the modified spherical harmonics2 of order $$$l$$$. They should also be invariant to allow comparisons across voxels and individuals. In this study, we evaluate and compare 3 candidate function basis sets for the radial domain (Fig.1):
1) SBF: Spherical Bessel functions $$$j_l(k\,q)$$$, with zero-derivative boundary condition. These form a natural complement to the spherical harmonics: combined, they facilitate the Fourier transform in spherical coordinates, hence maintaining a direct relation with the ensemble average propagator3. However, a discrete function basis can only represent the signal in a bounded domain $$$q<q_{max}$$$, with either a zero-value or zero-derivative boundary condition at this edge4.
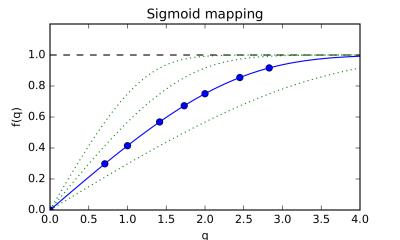
2) RSBF: Reparametrized Bessel functions. By introducing a reparameterisation of $$$q\in[0,+\infty]$$$ to $$$u\in[0,1]$$$ by means of a sigmoid mapping, the discrete Bessel functions can be used with zero-value boundary condition at $$$u=1$$$. This mapping is defined such that free diffusion with diffusivity $$$d$$$ maps exactly onto the 0th order basis function $$$j_0(k_1\,u)$$$ (Fig.2). The optimal value of this scaling parameter $$$d$$$ is determined by minimizing the fitting residuals over the entire brain.
3) SHORE: In contrast to the original SHORE literature5,6, we fix and optimize the diffusion scale for the entire image rather than in each voxel separately, to satisfy our requirements for an invariant basis.
All bases were compared in terms of their residual mean square error (RMSE) in simulations (mono-exponential decay with ADC between 0.1-3.0 µm2/ms, sampled at b-values 0, 400, 1000, and 2600 s/mm2 7, 100 instances with SNR=20 Gaussian noise) and in adult brain data (healthy volunteer, 7$$$\times$$$50 diffusion-sensitizing gradients at b=500, 1000, 2000, 3000, 4000, 6000, and 8000 s/mm2, 7 b=0 images).
Results
In simulations, the optimal scale parameter is $$$d=$$$ 0.4 for RSBF and $$$d=$$$ 1.1 for SHORE, resulting in RMSE across a dense range of $$$q$$$-values of 46.8 (SBF), 46.0 (RSBF), and 48.3 (SHORE), with a good fit for ADCs between 0.5-3.0 µm2/ms (Figure 3). SBF undershoots at high $$$q$$$ due to the zero-derivative boundary condition.
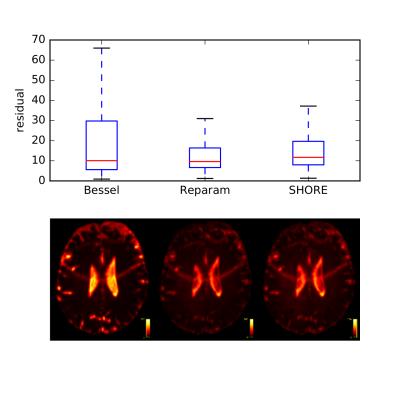
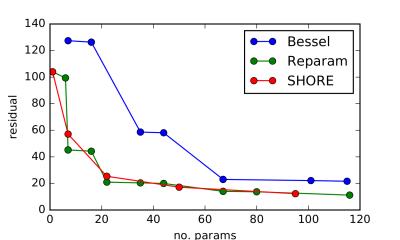
In the in vivo data, the optimal scale parameters were $$$d=$$$ 0.3 (RSBF) and 0.8 (SHORE) respectively, with RSBF and SHORE exhibiting the lowest RMSE. A good fit was obtained across white and grey matter, with increased residuals in regions of very high or low ADC (Fig.4). RSBF and SHORE performed similarly for varying numbers of parameters (Fig.5).
Discussion
These results underscore the fundamental need to tune the scale of the basis functions to the data at hand. In SHORE, tuning is typically done per voxel, based on the ADC. However, this is undesirable as it results in different basis functions for every voxel, making comparisons difficult. However, our results suggest that a single fixed scale can be used for the entire image with good accuracy in white and grey matter.
The SBF basis is limited by the appropriateness of the boundary conditions necessary to discretise the basis. Neither the zero-value or zero-derivative conditions are physically realistic at reasonable values of $$$q_{max}$$$, and furthermore introduce a dependency of the basis on parameters of the acquisition. In contrast, RSBF and SHORE can be tuned to the properties of the intrinsic signal (via the scale parameter $$$d$$$), allowing for comparisons across different acquisition parameters.
In terms of RMSE, RSBF performed best in simulation, but similarly to SHORE in vivo.
Conclusion
RSBF and SHORE can faithfully represent the DWI signal with low numbers of parameters, and can be tuned to the properties of the signal independently of acquisition parameters. Further work will investigate the relative merits of these two candidate bases.Acknowledgements
ERC funded dHCP project (Grant Agreement no. 319456) and MRC strategic funds (MR/K006355/1) and the GSTT BRC.References
1. Tuch D. Q-ball imaging. Magn. Reson. Med. 52(6): 1358–1372 (2004).
2. Descoteaux M, et al. Apparent diffusion coefficients from high angular resolution diffusion imaging: Estimation and applications. Magn. Reson. Med. 56(2): 395–410 (2006).
3. Hosseinbor AP, et al. Bessel Fourier Orientation Reconstruction: An Analytical EAP Reconstruction Using Multiple Shell Acquisitions in Diffusion MRI. Proc. of MICCAI 2011. LNCS 6892:217-225 (2011).
4. Wang Q, et al. Fourier Analysis in Polar and Spherical Coordinates. Technical Report (2008).
5. Ozarslan E, et al. Simple Harmonic Oscillator Based Reconstruction and Estimation for Three-Dimensional Q-space MRI. Proc. ISMRM (2009).
6. Ozarslan E, et al. Mean Apparent Propagator (MAP) MRI: A novel Diffusion Imaging Method for Mapping Tissue Microstructure. NeuroImage 78 (2013): 16-32.
7. Tournier J-D, et al. Data-driven optimisation of multi-shell HARDI. Proc. of ISMRM 23:2897 (2015).
Figures
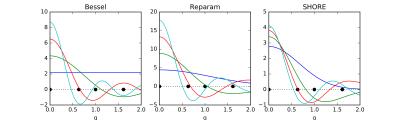
Fig. 1: Candidate radial function bases w.r.t. $$$q$$$ for the simulated b-value scheme (black dots). Left: spherical Bessel functions (SBF) with zero-derivative boundary condition at $$$q_{max}$$$. Middle: reparameterised spherical Bessel functions (RSBF) after sigmoid mapping of $$$q$$$ to the unit interval, with scale $$$d =$$$ 0.3. Right: the SHORE basis functions with scale $$$d =$$$ 1.1.