1809
Quantifying Reconstruction Uncertainty with Image Quality Transfer1Computer Science, University College London, London, United Kingdom, 2Microsoft Research Cambridge, 3Institute of Neurology, University College London
Synopsis
Image quality transfer employs machine learning techniques to enhance quality of images by transferring information from rare high-quality datasets. Despite its successful applications in super-resolution and parameter map estimation of diffusion MR images, it still remains unclear how to assess the veracity of the predicted image in practice, especially in the presence of pathology or features not observed in the training data. Here we show that one can derive a measure of uncertainty from the IQT framework and demonstrate its values as a surrogate measure of reconstruction accuracy (e.g. root mean square error).
Background
Image quality transfer (IQT) aims to enhance low-quality images by transferring information from rare high-quality datasets. Previous work demonstrate the potential of IQT in two applications. The first is super-resolution of DTI and MAP-MRI; [1] shows superior predictive accuracy over standard interpolation techniques and [2] demonstrates its benefits in the downstream application of tractography. The second is parameter mapping where IQT is applied to estimate NODDI and SMT parameters, which require multi HARDI shells, from DTIs fitted to single-shell data.Purposes
One key problem overlooked in the previous work [1,2] is the quantification of reconstruction uncertainty. In particular, when the input image contains unseen effects such as pathology, the performance is questionable and a surrogate measure of accuracy is in demand. Here we propose a method of quantifying uncertainty associated with IQT prediction, and show it highly correlates with accuracy. We demonstrate through super-resolution of DTIs of both healthy and pathological brains.
Method
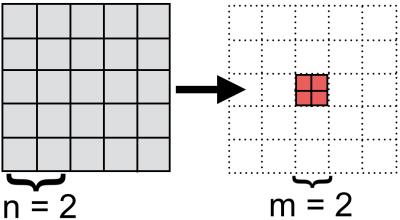
IQT formulates super-resolution as patch-regression where the input low-res image is split into small cubic patches of $$$5^3$$$ voxels and the corresponding high-res patches of $$$2^3$$$ voxels are estimated at the central voxels of these low-res patches (see figure 1). The current implementation of IQT employs a variant of regression trees [3], trained on matched pairs of DTI patches from down-sampled high-resolution images of 8 HCP subjects [4].
A regression tree is a piecewise probabilistic model; during super-resolution, it allocates each input patch to a subspace with the most similar set of observations (e.g. ‘white matter’ and ‘CSF’ subspaces) and infer the most likely high-res patch from the corresponding probability distribution. We propose to quantify the uncertainty over the tree output as the variance of this distribution.
The behaviour of uncertainty depends on the component model, and here we consider two types; maximum likelihood (ML) linear model used in the original IQT [1] and the Bayesian linear model in [5]. Given a new input $$$x$$$, the uncertainty of the former is given by the average error of fit computed on the training examples in the assigned subspace, while that of the latter is also modulated by a form of Mahalanobis distance of $$$x$$$ from the training set. In other words, the ML uncertainty quantifies the average accuracy in similar training instances, whereas Bayesian uncertainty also accounts for the degree of familiarity of the new input.
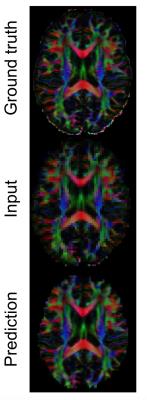
We first super-resolve a down-sampled $$$2.5$$$mm DTI of another HCP subject to recover the original resolution $$$1.25$$$mm (figure 2). We also test on clinical images of Multiple Sclerosis patients of resolution $$$2.0$$$mm, using trees trained on healthy HCP subjects. Lastly, we investigate how well uncertainty can determine sufficiently accurate voxels in the predicted high-res image. We define the `usable’ voxels as the ones with reconstruction error smaller than a fixed value, and want to select them from the rest by thresholding on the uncertainty. We vary the decision threshold on uncertainty to compute probability of hit and false alarm
Results
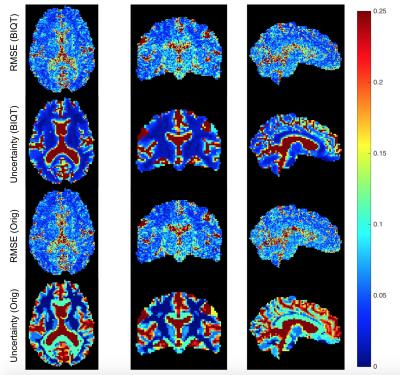
Figure 3 visualises uncertainty and reconstruction errors on a test HCP subject for the original IQT and BIQT. The uncertainty maps are in agreement with the reconstruction accuracy; more so for BIQT which can capture subtle variations in accuracy within white matter.
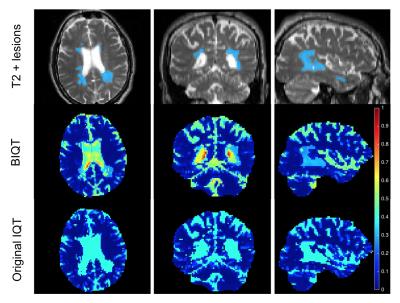
Figure 4 shows that the uncertainty map of BIQT identifies previously unseen pathology by assigning higher uncertainty with respect to the healthy tissues; pathological patches are sent into ‘white matter’ subspace, and its abnormality is quantified by high Mahalanobis distance. The uncertainty is higher on the CSF than the lesions in accordance with the high noise in the region. By contrast, IQT trees assign pathology to the CSF subspace and indicate the corresponding fixed uncertainty which is less informative.
The strong curvilinear features of the ROC curves (figure 5) show that our uncertainty measures are significantly better than random guess in discriminating accurate voxels in the estimated image. Although the ROC curves are very similar between Bayesian and original IQT, the continuous nature of the BIQT uncertainty (figure 5 (b)) allows for a fine quality control in contrast with the highly discretised uncertainty of the original method.
Discussion
We show that the variance of predictive distributions provides a useful measure of uncertainty in the IQT predictions, which qualitatively displays high correspondence with accuracy, and is robust enough to highlight unobserved pathology. Careful quantitative analysis (figure. 5) potentially enables the use of uncertainty in carving out usable regions in the predicted image for downstream applications such as tractography, registration and neurosurgical planning.Acknowledgements
This work was supported by Microsoft scholarship. Data were provided in part by the HCP, WU-Minn Consortium (PIs: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by NIH and Wash. U. The MS data were acquired as part of a study at UCL Institute of Neurology, funded by the MS Society UK and the UCL Hospitals Biomedical Research Centre (PIs: David Miller and Declan Chard).References
[1] D. C. Alexander, D. Zikic, J. Zhang, H. Zhang, A. Criminisi. Image quality transfer via random forest regression: applications in diffusion MRI. Proceedings MICCAI 225-232 2014
[2] D.C. Alexander, A. Ghosh, S.A. Hurley, S.N. Sotiropoulos. Image quality transfer benefits tractography of low-resolution data. Intl Society for Magnetic Resonance in Medicine (ISMRM) 2016
[3] A. Criminisi and J. Shotton. Decision forests for computer vision and medical image analysis. Springer, 2013.
[4] S.N. Sotiropoulos et al. Advances in diffusion MRI acquisition and processing in the human connectome project. Neuroimage 80 125–143 2013
[5] R. Tanno, A. Ghosh, F. Grussu, E. Kaden, A. Criminisi, D.C. Alexander. Bayesian image quality transfer. Proceedings MICCAI 265–273 2016
Figures