1807

Minimizing the error in finding peak orientations of fiber ODF in diffusion MRI using Nelder-Mead simplex method
Kuan-Hung Cho1, Chun-Hung Yeh2, Yi-Ping Chao3,4, Ching-Po Lin5, and Li-Wei Kuo1,6

1Institute of Biomedical Engineering and Nanomedicine, National Health Research Institutes, Miaoli, Taiwan, 2The Florey Institute of Neuroscience and Mental Health, Melbourne, Australia, 3Department of Computer Science and Information Engineering, Chang Gung University, Taoyuan, Taiwan, 4Department of Neurology, Chang Gung Memorial Hospital at Linkou, Taoyuan, Taiwan, 5Institute of neuroscience, National Yang-Ming University, Taipei, Taiwan, 6Institute of Medical Device and Imaging, National Taiwan University College of Medicine, Taipei, Taiwan

Synopsis

Discrete mesh search method is commonly used to determine fiber orientations by searching orientations corresponding local maxima of orientation distribution function (ODF). However, this method may produce extra errors relating to the number of sampling points of ODF in fiber orientation estimate. We address this problem and minimize the error of fiber orientation estimate by using Nelder-Mead simplex method. The results from computer simulation and phantom experiment show that Nelder-Mead simplex method gives accurate fiber orientation estimation better than discrete mesh search method with ODF sampling points less than 163,842.

PURPOSE

Fiber orientation is commonly determined by finding peaks of orientation distribution function (ODF) using a discrete mesh search method. This method only searches peaks on a finite number of ODF vertices and may introduce bias from real fiber orientation. This study aims to 1) address this problem by computer simulation and phantom experiments and 2) improve the accuracy of fiber orientation estimate using Nelder-Mead simplex method1.

METHODS

Computer simulations and phantom experiments are used to compare the angular error of fiber orientation determination by discrete mesh search and Nelder-Mead simplex methods. Three-dimensional Monte Carlo simulations were performed to simulate water molecular diffusion inside a single impermeable cylinder with diameter of 5 μm with total reflection rule on boundary2. The cases of single fiber and two-fiber crossing at 90o were simulated respectively. The ground truth of fiber orientation was randomly rotated in a 3D space for 100 repetitions. The diffusion signal attenuation was then calculated based on the pulsed-gradient spin-echo sequence3 with δ=45 ms, Δ=55 ms and b=4000 s/mm2. High-angular resolution diffusion MRI (HARDI) data was generated with 80 non-collinear gradient directions equally distributed on hemisphere in q-space. Gaussian noise is added to complex signal to generate data with different SNR.

A unidirectional phantom model was built by densely packing water-filled capillaries with inner/outer diameters of 20/90 μm into a sheet for phantom experiment4 and two bundles of capillaries were stacked onto each other to form two-fiber crossing at 90 degrees5 (Figure 1). HARDI data was acquired on a 9.4 T scanner (BioSpec, Bruker, Ettlingen, Germany) using a pulse-gradient stimulated-echo sequence with Δ=100 ms, δ=3 ms, b=4,000 s/mm2 and 160 non-collinear gradient directions equally distributed on a shell.

Q-ball imaging with spherical harmonic basis is used to reconstruct fiber ODF6. The maximum order of spherical harmonics was set to 8. ODF was reconstructed with 162, 642, 2,562, 10,242, 40,962, and 163,842 points respectively. We first estimated the local maximum of diffusion ODF by discrete mesh search method, and then one of the meshes containing the local maximum point was selected as a starting simplex for Nelder-Mead method to refine the estimation of local maximum.

RESULTS

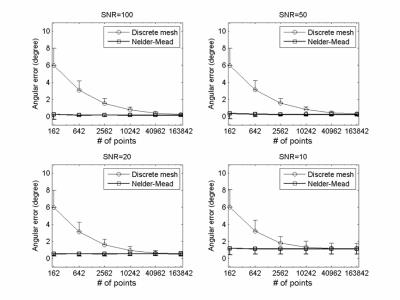
Figure 2 shows the simulation result of single fiber case. When using the discrete mesh search method, the mean and standard deviation of angular error both decreased while increasing the number of vertices for ODF reconstruction. By contrast, the Nelder-Mead simplex method improves fiber orientation for all levels of SNR, independently of the number of ODF vertices.

Figure 3 shows the result from unidirectional phantom. The estimated fiber orientation using the discrete mesh search method again resulted in larger error from ground truth with fewer ODF vertex number, and the error reduced as ODF vertex number increased. The Nelder-Mead simplex method showed significant improvement in finding the peaking orientation of ODF. It should be noticed that both methods show a minimum angular error about 5o, which may come from the estimate error of fiber orientation from T2WI.

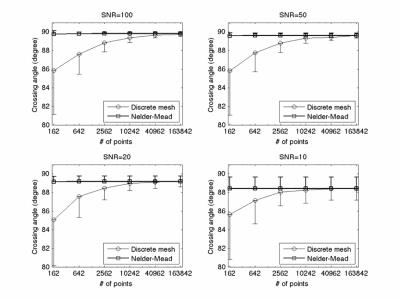
Figure 4 shows the simulation result of the case of two-fiber crossing at 90o. The underestimate and variation of crossing angle by discrete mesh search method become greater with fewer ODF vertex number while Nelder-Mead simplex method provides good estimate of fiber crossing with all levels of SNR and all ODF vertex numbers.

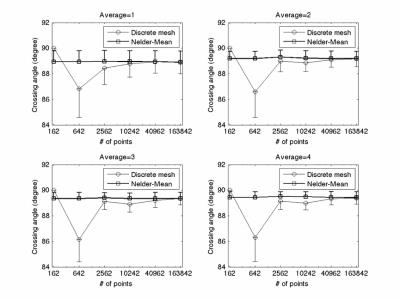
Figure 5 shows the results from crossing phantom. Nelder-Mead simplex method still provides good and consistent estimate of fiber crossing angle for all averages and ODF vertex numbers. Except the case of 162 ODF vertices, an increase of underestimate and variation of crossing angle with fewer ODF vertex number can also observed with discrete mesh search method. The Discrete mesh search method with 162 ODF vertices solves exact the same crossing angle in all voxels owing to relatively low angular resolution (about 16o) with 162 points.

DISCUSSION & CONCLUSION

Our results shows that Nelder-Mead simplex method can reduce estimate errors by using discrete mesh search method. Although discrete mesh search method with 163,842 ODF vertices can estimate fiber orientation as accurate as Nelder-Mead simplex method, the calculation time is much longer than Nexlder-Mead simplex method with fewer ODF vertices. In most of previous studies discrete mesh search method was used with hundreds of ODF sampling points that can make significant error in estimating fiber orientation. This estimate error would possibly result in biased fiber pathway using fiber tactography or inaccurate interpretation for brain structural network analysis. In conclusion, Nelder-Mead simplex method could significantly improve the accuracy of fiber orientation estimate from diffusion ODF comparing to discrete mesh search method.

Acknowledgements

The authors would are grateful to the National Health Research Institutes for support (NHRI-PP-06).

References

1. Nelder, J. A. and R. Mead (1965). A Simplex Method for Function Minimization. 7: 308-313.

2. Yeh, C. H., J. D. Tournier, et al. (2010). "The effect of finite diffusion gradient pulse duration on fibre orientation estimation in diffusion MRI." Neuroimage 51(2): 743-51.

3. Stejskal, E. O. (1965). "Use of Spin Echoes in a Pulsed Magnetic-Field Gradient to Study Anisotropic, Restricted Diffusion and Flow." The Journal of Chemical Physics 43(10): 3597-3603.

4. Cho, K. H., C. H. Yeh, et al. (2008). "Evaluation of the accuracy and angular resolution of q-ball imaging." Neuroimage 42(1): 262-71.

5. Yeh, C. H., K. H. Cho, et al. (2008). "Reduced encoding diffusion spectrum imaging implemented with a bi-Gaussian model." IEEE Trans Med Imaging 27(10): 1415-24.

6. Hess, C. P., P. Mukherjee, et al. (2006). "Q-ball reconstruction of multimodal fiber orientations using the spherical harmonic basis." Magn Reson Med 56(1): 104-17.

Figures

Figure 1.T2WI of unidirectional phantom (left, reprinted from reference 4) and 90o crossing phantom (right, reprinted from reference 5).

Figure 2. The plot of Angular errors (y-axis) of fiber orientation estimate by discrete mesh search method and Nelder-Mead simplex method versus different ODF sampling points (x-axis) with different SNR using computer simulation. Angular error is calculated as the angle between reconstructed fiber orientation and ground truth. The open circle and square are the mean value of angular error from 100 repetitions for discrete mesh search and Nelder-Mead simplex search respectively. The error bar represents the standard deviation of angular errors from 100 repetitions.

Figure 3. The plot of angular errors (y-axis) of fiber orientation estimate from 140 voxels of unidirectional phantom versus the number of ODF sampling points (x-axis) with different number of average. Angular error is calculated as the angle between the reconstructed fiber orientation and the orientation measured from high resolution T2-weighted image. The open circle and square are the mean value of angular error from 140 voxels for discrete mesh search and Nelder-Mead simplex search respectively. The error bar represents the standard deviation of angular errors from 140 voxels.

Figure 4. The plot of crossing angles (y-axis) of two crossing fibers at 90o by discrete mesh search method and Nelder-Mead simplex method versus different ODF sampling points (x-axis) with different SNR using Monte-Carlo simulation. The open circle and square are the mean value of crossing angles from 100 repetitions for discrete mesh search and Nelder-Mead simplex search respectively. The error bar represents the standard deviation of crossing angles from 100 repetitions.

Figure 5. The plot of crossing angles (y-axis) of fiber orientation estimate from 56 voxels of 90o crossing phantom versus the number of ODF sampling points (x-axis) with different number of average. The open circle and square are the mean value of angular error from 56 voxels for discrete mesh search and Nelder-Mead simplex search respectively. The error bar represents the standard deviation of crossing angles from 56 voxels.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
1807