1797
Multi-Tensor Filtering based on Expectation-Maximization Framework1Computer Science, Université de Sherbrooke, Sherbrooke, QC, Canada, 2Computational Radiology, Harvard Medical School, Boston, MA, United States, 3ICTEAM, Université catholique de Louvain, Louvain-La-Neuve, Belgium
Synopsis
In this abstract, we introduce a new multi-tensor regularization and denoising technique based on Expectation-Maximization framework. To reduce filtering blurring effect and preserve sharp edges, we incorporated anisotropic regularization weight to the framework. We also utilize a tensor similarity metric, made from a quaternion representation, to improve the regularization and preserve tensor characteristics. Finally, we evaluate and compare filtering methods using a diffusion MRI synthetic phantom and in-vivo acquisition.
Introduction
Several tensor regularization and filtering method have been proposed to increase the spatial consistency of Diffusion Tensor Image (DTI)[1,2,3]. However, these methods are limited to a single tensor field. Moreover, DTI is unable to represent crossing regions, known to occur in 60% to 90% of white matter[4,5].
Diffusion Compartment Imaging (DCI) models have been proposed to overcome the single tensor representation limitation, and better characterize the brain micro-structure (NODDI[6], CHARMED[7], DIAMOND[8]...). Among them, DCI models, such as the multi-tensor model or DIAMOND[8], produce multi-tensor fields to represent each fascicle in each voxel. Although, these approaches involve complex optimization procedures and are highly sensitive to noise.
Pasternack et al[9] proposed a regularization method that separately ensures smoothness of fiber shape, orientation and fraction. Also, Sotiropoulos et al[10] suggested a regularization method to improve the estimation, but limited to a bi-tensors model. Recently, Taquet et al[11] put forward an Expectation-Maximization (EM) framework, based on Gaussian mixture model simplification, to interpolate and average multi-tensor fields.
Objective
In this work, we introduce a new multi-tensor regularization methods, based on the theoretical image filtering approach from Gabor[14] to Perona-Malik[15], in which computation between each elements are achieved using the multi-tensor computational framework developed by Taquet et al[11]. In addition, we incorporate an anisotropic regularization weight to reduce the blurring effect and preserve sharp edges. We also combine the EM framework with the quaternion tensor metric to preserve characteristics of each tensor in the multi-tensor field[12]. Afterward, we compare and analyze filtering results using a diffusion MRI (dMRI) phantom with different SNR. At last, we illustrate multi-tensor reconstruction, from an in-vivo DCI acquisition, with and without filtering.Method
To enhance image quality and extract features, Gabor suggested to convolve the image with a gaussian kernel[14]. In a discrete domain, this formulation is equivalent to a heat diffusion equation, where multiple applications is proportional to a single application with an increased gaussian kernel size ($$$\sigma_r$$$). To avoid the blurring effect and preserve sharp edges, Perona-Malik[15] presented an anisotropic filtering method based on the neighbors intensity distance and gradient orientation.
In our case, each element of the image is not a scalar but a multi-tensor model. We propose to extend the image filtering techniques of Gabor[14] and Perona-Malik[15] to multi-tensor field, by utilizing the EM framework of Taquet et al[11]. To improve the regularization and preserve tensor characteristics, we integrated the quaternion distance metric between two tensors, from Collard et al[12], by considering:$$D(a,b)=min\left(\log\left(\frac{\lambda_1^a}{\lambda_3^a}\right),\log\left(\frac{\lambda_1^b}{\lambda_3^b}\right)\right)\arccos(\|{\mathbf{e}_1^a\cdot\mathbf{e}_1^b}\|)+\sum_{i=1}^3\left|\log\left(\frac{\lambda_i^a}{\lambda_i^b}\right)\right|,$$where$$$\,\lambda_j^x\,$$$and $$$\,\mathbf{e}_j^x\,$$$is the$$$\,j\,$$$ eigenvalue and eigenvector of tensor$$$\,x$$$, eigenvalues are sorted in decreasing order.
To further improve the filtering and preserve sharp edges, inspired by [2,15,16], we incorporate an iterative anisotropic weighting to the EM algorithm, by considering the following similarity measure between two tensors:$$S(a,b)=G_{\sigma_d}(D(a,b)).$$
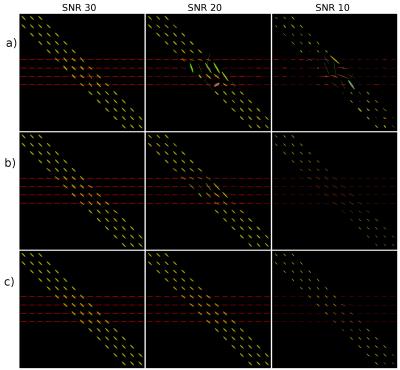
For the evaluation, we used a synthetic generated phantom (Figure#1) at various SNR(30,20,10). We also acquired an dMRI (cusp90) for the in-vivo DCI estimation. Both multi-tensor field were estimated using DIAMOND[8].
To analyze results, we filtered the noisy DCI estimation for each method, with different parameters, on many iterations. Once the tensor field is filtered, we computed the average error by comparing the result to the ground truth, using the tensor minimum angle error.
Result
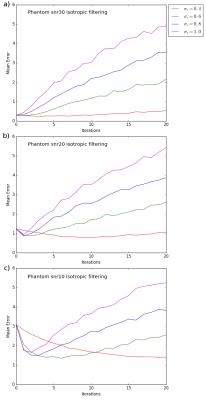
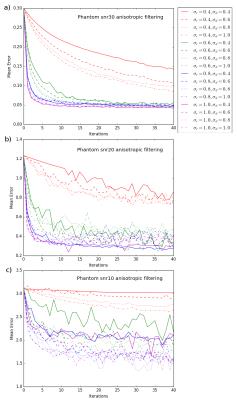
Figure#2 show the error evolution, for the multi-tensor field, using an isotropic averaging approach after repetitive application[11,13]. Figure#3 illustrate the same error but using our edge preserving method. Finally, we present filtering results on the phantom (Figure#4) and the in-vivo data (Figure#5).Discussion
As we can see in Figure#2-4, the initial method reduce noise from tensor field with few iterations, but afterward tend to blur edges and oversmooth causing the error to increase significantly. This is expected from an iterative isotropic averaging approach. Because of the EM algorithm, we observe that multiple iterations is not exactly equivalent to an increased$$$\,\sigma_r$$$. Moreover, the proposed anisotropic weighting method improved the resulting multi-tensor field but required more iterations (Figure#3-4). In Figure#4 at SNR10, even though the initial estimation is very noisy, both methods are able to reconstruct the crossing region. Like most anisotropic filter, our algorithm results are dependent of the chosen parameters. If sigma is not adapted to the SNR, the non-linear filtering might oversmooth or not be able to denoise.Conclusion
Filtering a multi-tensor field can enhance the spatial consistency of the image. Our proposed filtering method is able to denoise the multi-tensor field and preserve sharp edges. Still, depending on the parameters and number of iterations, filtering may blur the multi-tensor field. In future work, it would be interesting to automatically estimate the local SNR and select suitable parameters.Acknowledgements
This work was supported by grants from the NIH (U01 NS082320; R01 NS079788; R01 EB013248; R01 EB019483; and R21 EB012177).References
[1] Tschumperlé, David, and Rachid Deriche. "Diffusion tensor regularization with constraints preservation." Computer Vision and Pattern Recognition, 2001. CVPR 2001. Proceedings of the 2001 IEEE Computer Society Conference on. Vol. 1. IEEE, 2001.
[2] Hamarneh, Ghassan, and Judith Hradsky. "Bilateral filtering of diffusion tensor magnetic resonance images." IEEE Transactions on Image Processing 16.10 (2007): 2463-2475.
[3] Baust, Maximilian, et al. "Combined Tensor Fitting and TV Regularization in Diffusion Tensor Imaging based on a Riemannian Manifold Approach." (2016).
[4] Vos, Sjoerd B., et al. "The influence of complex white matter architecture on the mean diffusivity in diffusion tensor MRI of the human brain." Neuroimage 59.3 (2012): 2208-2216.
[5] Jeurissen, Ben, et al. "Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging." Human brain mapping 34.11 (2013): 2747-2766.
[6] Zhang, Hui, et al. "NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain." Neuroimage 61.4 (2012): 1000-1016.
[7] Assaf, Yaniv, and Peter J. Basser. "Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain." Neuroimage 27.1 (2005): 48-58.
[8] Scherrer, Benoit, et al. "Characterizing the distribution of anisotropic micro-structural environments with diffusion-weighted imaging (DIAMOND)." International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer Berlin Heidelberg, 2013.
[9] Pasternak, Ofer, et al. "Variational multiple-tensor fitting of fiber-ambiguous diffusion-weighted magnetic resonance imaging voxels." Magnetic resonance imaging 26.8 (2008): 1133-1144.
[10] Sotiropoulos, Stamatios N., et al. "A regularized two-tensor model fit to low angular resolution diffusion images using basis directions." Journal of Magnetic Resonance Imaging 28.1 (2008): 199-209.
[11] Taquet, Maxime, et al. "A mathematical framework for the registration and analysis of multi-fascicle models for population studies of the brain microstructure." IEEE transactions on medical imaging 33.2 (2014): 504-517.
[12] Collard, Anne, et al. "Anisotropy preserving DTI processing." International journal of computer vision 107.1 (2014): 58-74.
[13] Taquet, Maxime, Benoit Scherrer, and Simon K. Warfield. "A Framework for the Analysis of Diffusion Compartment Imaging (DCI)." Visualization and Processing of Higher Order Descriptors for Multi-Valued Data. Springer International Publishing, 2015. 271-297.
[14] M. Lindenbaum, M. Fischer, and A. Bruckstein. On gabor contribution to image enhancement. Pattern Recognition, 27:1–8, 1994.
[15] P. Perona and J. Malik. Scale space and edge detection using anisotropic diffusion.IEEE Trans. Patt. Anal. Mach. Intell., 12:629–639, 1990.
[16] Cabeen, Ryan P., and David H. Laidlaw. "Bilateral filtering of multiple fiber orientations in diffusion MRI." Computational Diffusion MRI. Springer International Publishing, 2014. 193-202.
Figures