Purpose

Both the intravoxel incoherent motion (IVIM)¹ and the kurtosis² model are extensions to the monoexponential apparent diffusion coefficient (ADC) model for the evaluation of diffusion weighted imaging (DWI). The biexponential IVIM model considers flow effects in perfused tissue while the Kurtosis model takes non-Gaussian diffusion into account. Both models provide valuable information for the assessment of various pathologies such as cancer or stroke^3,4. Hence, the simultaneous access to the parameters of the combined IVIM-Kurtosis model is highly desirable. Different approaches have been used to overcome the poor fit stability of a conventional least squares regression (LSR) when applying the combined model, which is due to the number of unknown fit parameters. The purpose of this simulation study is to present an artificial neural network (ANN) approach for fitting the IVIM-Kurtosis model parameters and to compare it to an ordinary bounded LSR.

Methods

Four feed forward ANNs with 10 hidden layers were implemented differing in the signal-to-noise-ratio (SNR) of the datasets they were trained with (Neural Network Toolbox provided by Matlab R2014a). The input layer is fed with 16 signal intensities corresponding to the following b-values: b = {0, 10, 20, 40, 70, 100, 150, 200, 300, 500, 700, 1000, 1500, 2000, 2400, 2800} s mm^-2 . The output layer returns the parameter estimates for the IVIM-Kurtosis model: $$$S(b)=S_0\cdot(f\cdot\exp{(-b(D^*+D))}+(1-f)\cdot\exp{(-bD+Kb^2D^2/6)})$$$. The ANNs were trained with 20⁵ simulated DWI signals within the parameter ranges typical for brain tissue of S­₀ = {0, …, 1500}, f = {0, …, 0.14}, D = {0, …, 1.8} ∙ 10^-3 mm² s^-1, D* = {0.9, …, 17} ∙ 10^-3 mm² s^-1 and K = {0, …, 2} with additional zero mean Gaussian noise. Thereby the training SNR levels of 25, 50, 100 and 150 yielded the corresponding ANNs further referred to as ANN25, ANN50, ANN100 and ANN150. In a Monte-Carlo simulation noisy DWI signals (SNR = 200) were generated sweeping the range of each parameter while keeping the remaining parameters constant. These signals were evaluated with a conventional bounded LSR and the different ANNs. From the resulting correlation curves the systematic error was determined by the root mean squared error (RMSE) between a first order polynomial fit through the data and the ground truth. The statistical error was determined by the standard deviation with respect to the fit and the total error was calculated by the RMSE of the data with respect to the ground truth. All errors were calculated relative to the respective parameter means.

Results

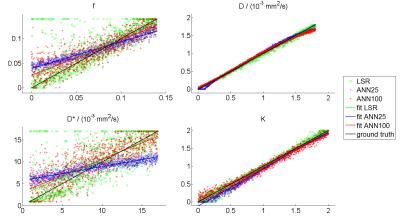
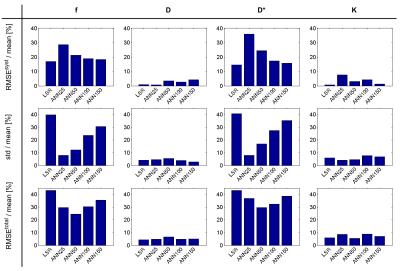
Figure 1 shows the correlation curves for all model parameters for LSR and ANN (i.e. ANN25 & ANN100). Both LSR and ANN show high correlations for D and K. For f and D* many non-converged values can be observed particularly for LSR while ANN shows higher systematical deviations. For D and K the correlation coefficient was between R=98% and R=100% for both LSR and ANN. By using ANN the correlation was significantly improved for f from R=77.0% (LSR) to R=86.1% (ANN100) and R=96.4% (ANN25). For D* the correlation was improved from R=70.3% (LSR) to R=80.5% (ANN100) and R=90.2% (ANN25). Figure 2 shows the systematic (first row), statistical (second row) and total errors (third row) for all parameters using LSR and each ANN. For D and K both LSR and ANN reveal comparable errors clearly below 10% and significantly smaller than for the parameters f and D*. For f and D* the lowest systematic error was achieved with LSR. Increasing the ANN training SNR led to a decreased systematic error and for high training SNR the systematic errors were comparable to LSR. On the contrary, the statistical errors of the ANNs were clearly decreased with decreasing training SNR and were significantly smaller compared to LSR. Overall, the total error was decreased by all ANNs compared to LSR with no apparent trend regarding the training SNR.

Discussion

It was successfully demonstrated that the proposed ANN approach performed superior over a conventional LSR in estimating diffusion parameters of the combined IVIM-Kurtosis model. While the choice of the evaluation method had a rather low impact on the performance of the D and K estimation, significant differences were found for f and D*. Here the correlation coefficients between estimates and ground truth could significantly be improved by using the proposed ANN method. The increased systematic error observed for ANN was traded for a simultaneously decreased statistical error resulting in an overall improved estimation. As a consequence the ANN approach appears preferable to a conventional LSR in providing valuable information for the assessment of brain pathologies such as cancer or stroke.

Acknowledgements

The first author is funded by the Carl-Zeiss-Stiftung in the form of a PhD scholarship.