1793
Robust mapping of diffusion parameters of the combined IVIM-Kurtosis-model using artificial neural networks in the human brain1Computer Assisted Clinical Medicine, Heidelberg University, Mannheim, Germany
Synopsis
In this work we present an artificial neural network (ANN) approach for the evaluation of the combined IVIM-Kurtosis model and robust mapping of the diffusion parameters in the human brain. Measuring seven healthy subjects the parameter map quality could be improved compared to an ordinary least squares regression by significantly reducing outliers and decreasing the variance while preserving the tissue contrast. An ROI-based analysis additionally showed a better agreement of the mean parameter values with the literature along with a better distinction between white and grey matter for the ANN approach.
Purpose
For the signal evaluation in diffusion weighted
imaging (DWI), various models are applied to describe the signal attenuation.
Besides the monoexponential apparent diffusion coefficient (ADC) model, the
biexponential intravoxel incoherent motion (IVIM) model1 considers
flow effects in perfused tissue and the Kurtosis model2
takes non-Gaussian diffusion into account. Each of the latter models has been
shown to be diagnostically conclusive in the assessment of pathologies in the
human brain such as cancer or stroke3,4. A
simultaneous access to the parameters of both models is therefore highly
desirable. Due to the number of unknown fit parameters of the combined IVIM-Kurtosis
model, the fit stability is low resulting in bad quality parameter maps when ordinary
least squares regression (LSR) is used. Different approaches, such as Bayesian
or multi-step fitting5,6,
have been used to overcome this issue. In this work, an artificial neural
network (ANN) approach for robust mapping of the IVIM-Kurtosis parameters is
presented and compared to conventional LSR in terms of outlier voxels, accuracy
and precision.Methods
Brain measurements of seven healthy subjects (two female, five male; 23-35 years) were performed on a Siemens Trio 3T MR-scanner with a 32-channel head coil. A double refocused echo planar imaging spin echo (EPI SE) sequence with 16 b-values (b = 0, 10, 20, 40, 70, 100, 150, 200, 300, 500, 700, 1000, 1500, 2000, 2400, 2800 s mm-2) in three orthogonal directions was used. The diffusion weightings were chosen to cover both b-values below 200 s mm-2 as a typical range, in which the perfusion effect plays a major role in the IVIM-model, as well as b-values above 1000 s mm-2, where the kurtosis has a significant effect on the signal. Additional parameters were TR = 3200 ms, TE = 133 ms, NA = 6, matrix size = 96 × 96 with an isotropic FOV = 200 mm and number of slices = 13 with thickness = 3 mm. The total acquisition time was approximately 15 min. The combined IVIM-Kurtosis model was used to describe the signal decay: $$$S(b)=S_0\cdot(f\cdot\exp{(-b(D^*+D))}+(1-f)\cdot\exp{(-bD+Kb^2D^2/6)})$$$. For evaluation two different ANNs were used, implemented with the Neural Network Toolbox provided by Matlab R2014a. The two ANNs were trained with simulated DWI datasets of SNR=25 (ANN25) and SNR=100 (ANN100) respectively. Additionally an ordinary bounded LSR approach was applied for comparison. For a region-of-interest (ROI) analysis the images were automatically segmented into grey matter (GM) and white matter (WM) with the Matlab toolbox SPM12.Results
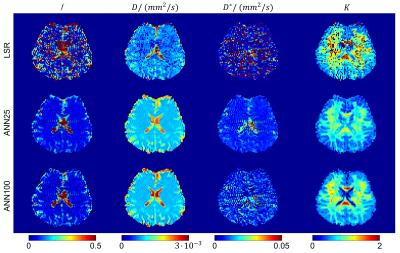
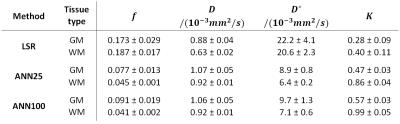
Figure 1 shows maps of the model parameters f, D, D* and K obtained with the bounded LSR as well as the two ANN approaches, ANN25 and ANN100. Both ANN methods produce smoother maps with less outliers while preserving tissue contrast. The fraction of outlier voxels was significantly reduced for f from 18 % (LSR) to 6 % (ANN25) and 13 % (ANN100), for D* from 30 % (LSR) to 7 % (ANN25) and 26 % (ANN100) and for K from 9 % (LSR) to 0 % (ANN25 & ANN100). Table 1 lists the inter-subject means and standard deviations of all model parameters in GM and WM obtained with each method. Standard deviations could significantly be reduced for the parameters f, D* and K when using ANN compared to LSR. According to a paired t-test (p < 10-3) significant differences between LSR and the ANNs (ANN25 & ANN100) were found for all parameters. ANN25 differed from ANN100 only in the K estimation. A paired t-test (p < 10-3) further showed that with ANN25 (ANN100) GM and WM could be distinguished for the parameters f, D, D* and K (f, D, and D*). Using LSR, the GM and WM discrimination was only possible for the D parameter.Discussion
The ANN approach tested in the in-vivo evaluation resulted in an apparently superior map quality compared to the ordinary bounded LSR method. The better recognisability of the underlying tissue structure results from a significant reduction of outliers accompanied by a reduced variance. Despite the lower variance, a better distinction between GM and WM was possible with ANN. While the parameter values for f, D* and K found with both ANNs are rather conform to literature values4,7, LSR significantly deviates. Comparing the ANNs with each other, ANN25 generally results in a higher parameter precision and a more successful minimization of outlier voxels. ANN100 on the other hand features a higher variance, while potentially leading to higher parameter accuracy. In conclusion the proposed ANN approach appears preferable to a conventional LSR in the assessment of brain pathologies, such as cancer or stroke, with the IVIM-Kurtosis model.Acknowledgements
The first author is funded by the Carl-Zeiss-Stiftung in the form of a PhD scholarship.References
1. Le Bihan, D., et al., MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology, 1986. 161(2): p. 401-407.
2. Jensen, J.H., et al., Diffusional kurtosis imaging: The quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine, 2005. 53(6): p. 1432-1440.
3. Bisdas, S., et al., Intravoxel incoherent motion diffusion-weighted MR imaging of gliomas: feasibility of the method and initial results. Neuroradiology, 2013. 55(10): p. 1189-1196.
4. Hui, E.S., et al., Stroke assessment with diffusional kurtosis imaging. Stroke, 2012. 43(11): p. 2968-2973.
5. Orton, M.R., et al., Improved intravoxel incoherent motion analysis of diffusion weighted imaging by data driven Bayesian modeling. Magnetic Resonance in Medicine, 2014. 71(1): p. 411-420.
6. Luciani, A., et al., Liver cirrhosis: intravoxel incoherent motion MR imaging—Pilot study 1. Radiology, 2008. 249(3): p. 891-899.
7. Federau, C., et al., Quantitative measurement of brain perfusion with intravoxel incoherent motion MR imaging. Radiology, 2012. 265(3): p. 874-881.
Figures