1787
Exploring the potentials and limitations of improved free-water elimination DTI techniques1Cognition and Brain Sciences Unit, MRC, Cambridge, United Kingdom, 2Haukeland University Hospital, Bergen, Norway, 3eScience Institute, The University of Washington, Seattle, WA, United States, 4Departments of Psychiatry and Radiology, Brigham and Women's Hospital, Harvard Medical School, Boston, MA, United States
Synopsis
Free-water diffusion tensor imaging (fwDTI) was previously proposed to remove CSF partial volume effects of measures based on the diffusion tensor. Nevertheless, this diffusion-weighted technique is still subject to several pitfalls. In this study, an improved algorithm to fit the fwDTI to data acquired with two or more diffusion-weighting gradients is proposed. This algorithm is then used to explore the advantages and limitations of suppressing free-water in synthetic and in vivo diffusion-weighted data.
Introduction
Typical diffusion-weighted imaging (DWI) is susceptible to partial volume effects: different types of tissue that reside in the same voxel are inextricably mixed. For instance, in regions near the cerebral ventricles or parenchyma, fractional anisotropy (FA) from diffusion tensor imaging (DTI) may be underestimated, due to partial volumes of cerebral spinal fluid (CSF)1. In aging or neurological disorder studies, removing CSF contamination is essential to quantify changes that are specifically related to brain tissue2,3. For single-shell, DTI-like acquisitions, the diffusion properties of the tissue can be separated from the isotropic diffusion of free-water in the CSF using the free-water elimination DTI (fwDTI) model1. Recently, an approach to estimate the model from multi-shell data was suggested4. The robustness of this approach was challenged by studies showing that noise can bias estimates towards neglecting the free-water component5 and inflating the tissue’s FA in brain regions of low tissue anisotropy4. In this study, we propose a novel procedure to fit the fwDTI model for data acquired with multiple b-values. We show that the proposed method improves robustness to noise. This algorithm is then used to study the parameter bias induced by regions with low anisotropy, and by restricted and hindered diffusion effects in the tissue not assumed by fwDTI's model.Methods
fwDTI model fitting: Similarly to previous procedures4, the fwDTI model is fitted to the diffusion-weighted signals $$$s_i$$$ using a non-linear least squares (NLS) approach. This approach is very sensitive to the initial guess of the model parameters $$$\gamma$$$, which can be computed by a grid search of the best weighted linear least squares (WLLS) solution of the model parameters. The selection of the initial guess was previously performed using the WLLS objective function4, however we suggest using the NLS objective function:
$$F_{NLS}=\frac{1}{2}\sum_{i=1}^{m}\left[s_{i}-S_{0}f\exp(-\sum_{j=2}^{4}W_{ij}D_{iso})-(1-f)\exp(-\sum_{j=1}^{7}W_{ij}\gamma_{j})\right ]^{2}$$
where $$$f$$$ is the fraction of free water in the voxel, $$$D_{iso}$$$ is the diffusivity of free water, and $$$W$$$ is a matrix containing the acquisition parameters4.
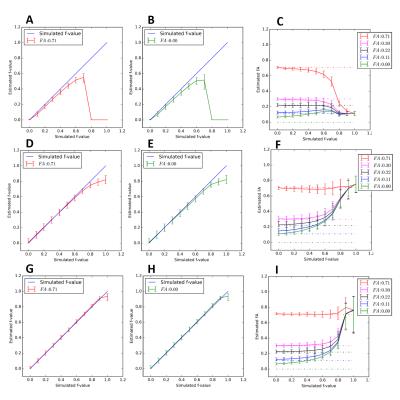
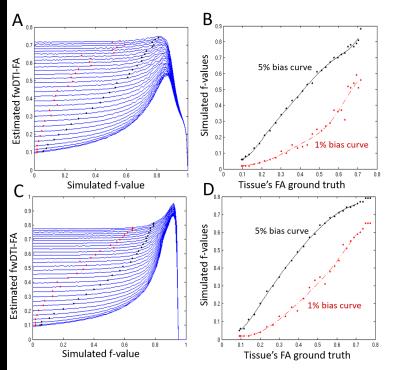
Simulations: To evaluate the performance of different fwDTI fitting algorithms, multi-compartmental simulations were first performed using the acquisition scheme and ground truth values proposed by4. To assess fwDTI effects in the presence of restricted and hindered diffusion, diffusion heterogeneity was incorporated by separately modelling intra- and extra-cellular compartments for a varying number of white matter fibers6. These simulations were then used to detect ground truth $$$f$$$ and FA values resulting in FA overestimation (see Fig.3 for more details).
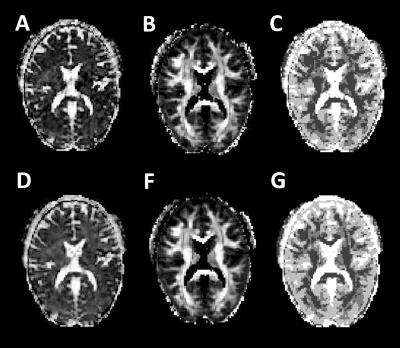
MRI experiments: DWI data were acquired on a Siemens 3T Trio (32-channel coil) using a TRSE sequence, 30 directions for b-values=500, 1500s/mm2 and two b=0)4. A second protocol had 30 directions for bvalues=1000, 2000s/mm2 and two b=0. To assess fwDTI-FA bias across different brain regions, in vivo fwDTI-$$$f$$$ and DTI-FA were compared to $$$f$$$ and FA ground truth values which results in fwDTI overestimation. Since DTI-FA and fwDTI-$$$f$$$ are always smaller than the tissue's FA and free-water volume fractions ground truth values, the estimated bias maps indicates the worst possible fwDTI-FA overestimation at each brain locations (see Fig.4 for more details).
Results and Discussion:
Using the approach for fwDTI initial guess estimation proposed here, and contrary to the previous approaches (Fig.1A-C)4,5, we no longer see underestimation of $$$f$$$ values (Fig.1D-F). The results from the NLS fitting approach that uses the proposed fwDTI initial guess estimates are shown in Fig.1(G-I).
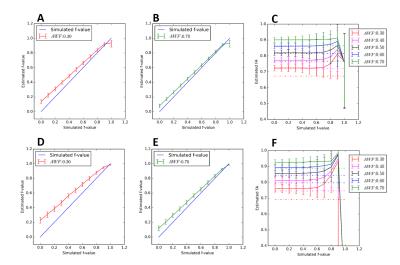
When restricted and hindered diffusion effects are taken into account, the fwDTI’s $$$f$$$ estimates are still proportional to the ground truth values. However, $$$f$$$ now also depends on the volume fraction of hindered diffusion (Fig.2A). For well-aligned fiber simulations, fwDTI-FA estimates seem to be invariant to free-water volume fractions up to $$$f$$$=0.6 (Fig.2B-C). When higher b-values are included in the acquisition, $$$f$$$ becomes more sensitive to the hindered compartment volume fractions (Fig.2D), while fwDTI-FA estimates remain independent up to medium range free-water contaminations (Fig.2E-F).
The lower $$$f$$$ values associated to fwDTI-FA overestimates of 1 and 5% are plotted as a function of fwDTI-FA ground truth (Fig.3B,F). In-vivo fwDTI measures are shown in Fig.4. The fwDTI bias map reveals that fwDTI-FA overestimation is lower that 5% for most white matter regions (Fig.4C,F).
Conclusion
Our modification of fwDTI fitting seems to provide useful information of the degree of water contamination, even though the fwDTI model does not take into account the restricted and hindered diffusion effects of tissue. While larger volume fractions of hindered diffusion are captured by the free-water volume fraction, measures of tissue-related diffusion (FA) seem relatively invariant to low/medium free-water volume fractions and result in relatively small bias for most white matter regions.Acknowledgements
This work was funded by Fundação para a Ciência e Tecnologia FCT/MCE (PIDDAC) under grant SFRH/BD/89114/2012.References
[1] Pasternak O, Sochen N, Gur Y, Intrator N, Assaf Y. Free water elimination and mapping from diffusion MRI. Magn Reson Med 2009; 62(3): 717-30. doi: 10.1002/mrm.22055.
[2] O’Donnell LJ, Pasternak O. Does diffusion MRI tell us anything about the white matter? An overview of methods and pitfalls. Schizophr Res. 2015; 161(1): 133–141 doi: 10.1016/j.schres.2014.09.007
[3] Pasternak O, Westin CF, Bouix S, Seidman LJ, Goldstein JM, Woo TUW, Petryshen TL, Mesholam-Gately RI, McCarley RW, Kikinis R, Shenton ME, Kubicki M. Excessive extracellular volume reveals a neurodegenerative pattern in schizophrenia onset. J Neurosci. 2012; 32(48):17365–17372.
[4] Hoy AR, Koay CG, Kecskemeti SR, Alexander AL. Optimization of a free water elimination two-compartment model for diffusion tensor imaging. NeuroImage 2014: 103; 323-333. doi: 10.1016/j.neuroimage.2014.09.053
[5] Bergmann Ø, Westin CF, Pasternak O. Challenges in solving the two-compartment free-water diffusion MRI model. Proceedings of the 24th Annual Meeting of the International Society for Magnetic Resonance Medicine; Singapore. May 7–13, 2016.
[6] Henriques RN, Correia MM, Nunes RG, Ferreira HA. Exploring the 3D geometry of the diffusion kurtosis tensor—Impact on the development of robust tractography procedures and novel biomarkers. NeuroImage 2015; 111: 85-99. doi: 10.1016/j.neuroimage.2015.02.004.
Figures