1783

Solving the free water elimination estimation problem by incorporating T2 relaxation properties
Quinten Collier1, Jelle Veraart1,2, Arnold J. den Dekker1,3, Floris Vanhevel4, Paul M. Parizel4, and Jan Sijbers1

1Vision Lab, University of Antwerp, Antwerp, Belgium, 2Center for Biomedical Imaging, Department of Radiology, New York University School of Medicine, New York, NY, United States, 3Delft Center for Systems and Control, Delft University of Technology, Delft, Netherlands, 4Department of Radiology, Antwerp University Hospital, Antwerp, Belgium

Synopsis

The free water elimination (FWE) model fitting problem is inherently ill-conditioned, leading to the need for solutions that can avoid or deal with these kinds of fitting problems. In this work, we evaluate a model extension to the FWE model that exploits the T2-relaxation properties and subsequently leads to a well-posed fitting problem that can be easily solved using standard estimation techniques.

Purpose

The free water elimination (FWE) diffusion model accounts for partial volume effects that occur when voxels in diffusion tensor imaging (DTI) volumes contain both a tissue and a free water compartment1-2. A major downside of FWE is that the model fitting problem is ill-conditioned, or, for isotropic diffusion, even ill-posed3-4. Therefore, FWE has previously been tackled with advanced parameter estimation techniques that incorporate, e.g., regularization2 or statistical priors5-6. These methods usually succeed in stabilizing the model fit but, as a trade-off, impose model assumptions that are likely to bias the results.

In this work, we exploit that the T2 relaxation times of white matter and cerebrospinal fluid are very different, i.e. approximately 70ms7 and 500ms8, respectively. By accounting for the associated TE dependency of the signal decay, the model parameters can be estimated more precisely, accurately, and robustly.

Methods

FWE models the diffusion weighted signal $$$S_i$$$ as:

$$S_i=S_0\left(\left(1-f\right)e^{-b_ig^T_iDg_i}+fe^{-b_id}\right)\hspace{1.5cm}[1]$$

with $$$S_0$$$ the non-diffusion weighted signal, $$$b_i$$$ and $$$g_i$$$ the diffusion weighting strength and direction respectively, $$$f$$$ the free water signal fraction, $$$D$$$ the diffusion tensor and $$$d=3\hspace{2mm}\mu m^2/ms$$$ the diffusivity of free water at body temperature. To solve this ill-conditioned problem, a relationship between the signal fraction $$$f$$$ and the actual volume fraction $$$F$$$ is introduced by accounting for the T2-values of the tissue $$$T2_{tissue}$$$ and free water $$$T2_{fw}$$$:

$$f=\frac{F\cdot e^{-TE/T2_{fw}}}{\left(1-F\right)\cdot e^{-TE/T2_{tissue}}+F\cdot e^{-TE/T2_{fw}}}.\hspace{1.5cm}[2]$$

$$$T2_{tissue}$$$ and $$$T2_{fw}$$$ can either be estimated or assumed to be known a priori. Estimation of the T2 relaxation times can be achieved from pure voxels from complementary data7 or even from the non-diffusion weighted images. For equation [2] to be useful, diffusion measurements with at least two different TEs need to be acquired.

In this work, first the Cramér-Rao lower bound (CRLB) was used to evaluate the FWE-T2 model with and without a priori known T2 values. The CRLB, which was derived assuming Gaussian distributed data, gives insight in the maximal attainable precision of the parameter estimates and their correlations. Note that for Gaussian distributed data the NLS estimator equals the maximum likelihood estimator, which is known to attain the CRLB asymptotically9. Next, the optimization space of the NLS estimator of the FWE-T2 model was studied together with corresponding Monte Carlo simulations. For both the FWE-T2 model and the standard FWE model, 1000 data sets contaminated with zero mean Gaussian distributed noise were generated. Finally, the effect of errors in the T2 assumptions on the resulting model parameter estimates was studied. Simulation settings include: SNR=20 on the non-diffusion weighted signal and $$$b=0,0.5,1\hspace{2mm}\mathrm{ms/\mu m^2}$$$ with 30 measurements per shell and 6 non-diffusion weighted images. For the FWE-T2 model, 2 TE values were used: TEmin = 65ms and a variable TEmax.

Results and discussion

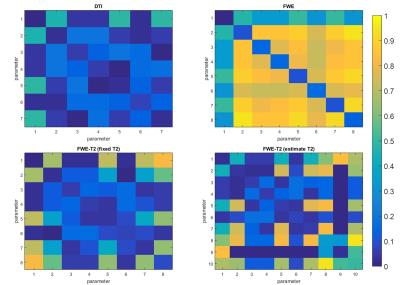
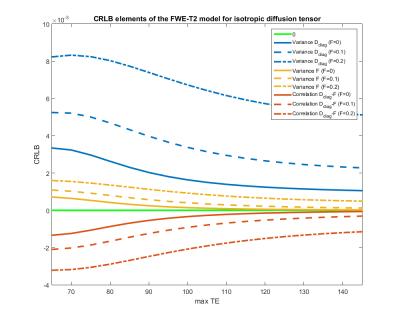
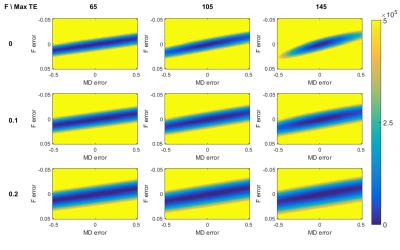
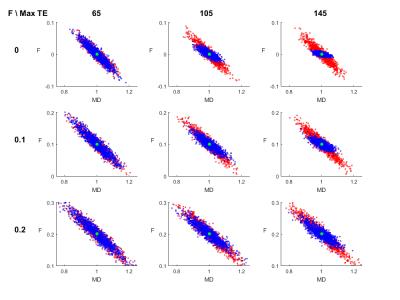
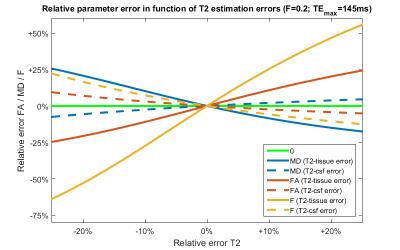
Figure 1 shows the coefficients of variation and correlation coefficients, derived from the CRLB matrix. The analysis of the extended model shows that effective decoupling of $$$F$$$ and $$$D$$$ is only achieved if T2s are known a priori. For the next experiments, we build upon that premise. Figure 2 shows the CRLB elements that correspond with the variance of $$$F$$$ and diagonal elements of $$$D$$$ and the covariance between $$$F$$$ and $$$D$$$. It is clear that both the variance and covariance decrease with a higher TEmax. This can also be seen in both the optimization space of the FWE-T2 model (Figure 3) and the results of the Monte Carlo simulations (Figure 4). For TEmax = TEmin = 65ms the FWE-T2 problem is reduced to the standard FWE model fitting problem and is consequently ill-posed as there is no unique minimum. With increasing TEmax the minimum gets better defined and the FWE-T2 model succeeds in substantially reducing the correlation between the mean diffusivity $$$MD$$$ and $$$F$$$ while at the same time improving the precision of both parameter estimates. Finally, Figure 5 shows that one should be careful when setting the T2-values, especially T2-tissue, as the other model parameters are strongly dependent on an accurate T2 estimation.

Conclusion

We showed that the FWE model fitting problem can become well-posed by exploiting the TE dependency of the diffusion-weighted signal decay in partial volume voxels that roots in the different T2 relaxation times of CSF and white matter. However, using a statistical analysis, we here demonstrate that the model relies on prior knowledge of the T2 values. The accurate estimation of those values will be of utmost importance due to the error propagation of the model.

Acknowledgements

No acknowledgement found.

References

[1] Pasternak O, Sochen N, Gur Y, Intrator N, & Assaf Y. Free water elimination and mapping from diffusion MRI. Magnetic Resonance in Medicine. 2009;62(3):717–30.

[2] Pierpaoli C & Jones D K. Removing CSF Contamination in Brain DT-MRIs by Using a Two-Compartment Tensor Model. Proc. Intl. Soc. Mag. Reson. Med. 12; 2004.

[3] Bergmann O, Westin C F, Pasternak O. Challenges in solving the two-compartment free-water diffusion MRI model. Proc. Intl. Soc. Mag. Reson. Med. 24; 2016.

[4] Collier Q, Veraart J, Jeurissen B, den Dekker A J, & Sijbers J. Theoretical study of the free water elimination model, Proc. Intl. Soc. Mag. Reson. Med. 23; 2015.

[5] Vallée E, Douaud G, Monsch A U, Gass A, Wu W, Smith S & Jbabdi S. Modelling free water in diffusion MRI. Proc. Intl. Soc. Mag. Reson. Med. 23; 2015.

[6] Collier Q, den Dekker A J, Jeurissen B, & Sijbers J. Robust DKI parameter estimation in case of CSF partial volume effects, Proc. Intl. Soc. Mag. Reson. Med. 24; 2016.

[7] Stanisz G J, Odrobina E E, Pun J, Escaravage M, Graham S J, Bronskill M J, & Henkelman R M. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magnetic Resonance in Medicine. 2005;54(3), 507–512.

[8] Piechnik S K, Evans J, Bary L H, Wise R G, & Jezzard P. Functional changes in CSF volume estimated using measurement of water T2 relaxation. Magnetic Resonance in Medicine. 2009;61(3), 579–586.

[9] van den Bos A. Parameter Estimation for Scientists and Engineers. Hoboken, New Jersey: John Wiley and Sons Inc.; 2007.

Figures

Figure 1: Coefficients of variation and correlation coefficients, derived from CRLB matrix, for the DTI, FWE, FWE-T2 (with fixed T2 values) and FWE-T2 (with T2 values to be estimated) models. Parameters are: $$$S_0$$$(1), $$$D_{xx}$$$(2), $$$D_{xy}$$$(3), $$$D_{xz}$$$(4), $$$D_{yy}$$$(5), $$$D_{yz}$$$(6), $$$D_{zz}$$$(7), $$$f$$$ or $$$F$$$(8), $$$T2_{tissue}$$$(9) and $$$T2_{fw}$$$(10). A diffusion tensor with $$$\text{MD}=1\mu m^2/ms$$$ and $$$\text{FA}=0.5$$$, free water volume fraction $$$F=0.1$$$, $$$T2_{tissue}=60\mathrm{ms}$$$ and $$$T2_{csf}=250\mathrm{ms}$$$ was assumed with $$$\text{TE}_{max}=145$$$.

Figure 2: Cramér-Rao lower bound elements in function of the highest TE value (lowest TE = 65 ms). The variance of $$$F$$$ (yellow) and the diagonal elements of $$$D$$$ (blue) and the covariance between the diagonal elements of $$$D$$$ and $$$F$$$ (red) are shown for 3 different $$$F$$$-values: 0 (solid line), 0.1 (dashed line) and 0.2 (point-dashed line). An isotropic diffusion tensor with $$$\text{MD}=1\mu m^2/ms$$$, $$$T2_{tissue}=60\mathrm{ms}$$$ and $$$T2_{csf}=250\mathrm{ms}$$$ was assumed.

Figure 3: The value of the NLS cost function for the FWE-T2 model fitting problem. The error of MD is plotted versus the error of $$$F$$$. The highest TE is varied between 65 (=lowest TE), 105 and 145. $$$F$$$ is varied between 0, 0.1 and 0.2. All values are truncated at 5e5 for visual clarity. An isotropic diffusion tensor with $$$\text{MD}=1\mu m^2/ms$$$, $$$T2_{tissue}=60\mathrm{ms}$$$ and $$$T2_{csf}=250\mathrm{ms}$$$ was assumed.

Figure 4: Scatter plots of Monte Carlo simulations of the estimates of $$$F$$$ and $$$\text{MD}$$$ for both the FWE-T2 model (blue) and the standard FWE model (red). The highest TE is varied between 65 (=lowest TE), 105 and 145. $$$F$$$ is varied between 0, 0.1 and 0.2. The true underlying parameter values are indicated with a green dot. An isotropic diffusion tensor with $$$\text{MD}=1\mu m^2/ms$$$, $$$T2_{tissue}=60\mathrm{ms}$$$ and $$$T2_{csf}=250\mathrm{ms}$$$ was assumed.

Figure 5: Relative error in $$$\text{MD}$$$ (blue), $$$\text{FA}$$$ (red) and $$$F$$$ (yellow) in function of the relative error in the assumption of $$$T2_{tissue}$$$ (solid line) and $$$T2_{csf}$$$ (dotted line). A diffusion tensor with $$$\text{MD}=1\mu m^2/ms$$$ and $$$\text{FA}=0.1$$$, free water volume fraction $$$F=0.2$$$, $$$T2_{tissue}=60\mathrm{ms}$$$ and $$$T2_{csf}=250\mathrm{ms}$$$ was assumed.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
1783