1782
Directional sensitivity of anomalous diffusion assessed using a tensorial fractional motion model1Center for MRI Research, Peking University, Beijing, People's Republic of China, 2State Key Laboratory of Cognitive Neuroscience and Learning, Beijing Normal University, Beijing, People's Republic of China, 3MR Research China, GE Healthcare, Beijing, People's Republic of China
Synopsis
Anisotropic diffusion in the nervous system is most commonly modeled by the apparent diffusion tensor, which is based on normal diffusion theory. However, the departure of the diffusion-induced signal attenuation from the mono-exponential form indicates the existence of anomalous diffusion. The fractional motion (FM) model, which is considered as the appropriate anomalous diffusion theory for biological tissues, has been applied to diffusion MRI. However, the directional sensitivity of the FM model in biological tissues remains elusive. In this study, this issue was addressed via tensor analysis in analogy with the diffusion tensor.
Purpose
Conventional diffusion MRI (dMRI) assumes the diffusion in biological tissues as a normal diffusion process and thus relates the signal attenuation with the apparent diffusion coefficient (ADC) in a mono-exponential form, as $$$S/S_0=\exp(-b\cdot ADC)$$$ . However, It has been shown that the diffusion-induced signal attenuation deviates from the mono-exponential form in biological tissues1. Recently, the dMRI framework based on the fractional motion (FM) model has been proposed2, which was considered more appropriate in describing the anomalous diffusion processes in living cells3,4. The diffusion process in nervous system was found directionally dependent5,6 and the apparent diffusion tensor, which is a generalization of ADC in normal diffusion theory, is used to describe this phenomenon7. However, the directional sensitivity of the FM model in biological tissues remains elusive. In this study, the tensor model was adopted for FM-related parameters to explore their directionalities.Methods
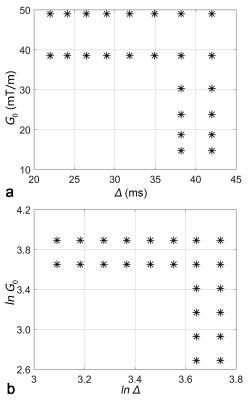
Fifteen healthy subjects (seven males and eight females; mean age, 22.4±1.3 years) were recruited in this study, consent forms were obtained prior to the scan. The acquisition was performed on a 3T GE Discovery MR750 MRI scanner (GE Healthcare, Milwaukee, Wisconsin) equipped with an 8-channel head coil. Acquisition parameters were: TR/TE=4000ms/90ms; accelerating-factor=2; field-of-view=24cm×24cm; matrix size=80×80; slice-thickness=3 mm; and number-of-excitations=2. The diffusion gradients were applied successively in 12 non-collinear directions. In each direction, after b0 image, 24 non-zero b-values ranging from 324 to 4782 s/mm2, were produced by varying the diffusion gradient amplitudes (G0), the gradient duration (δ) and the separation time (Δ) while keeping $$$\delta/\Delta=0.7$$$. This acquisition scheme is illustrated in Figure 1. In addition, a sagittal T1-weighted structural image (TR/TE = 600ms/12ms, 1mm isotropic voxel resolution) was acquired as an anatomical reference for each subject.
After correction for eddy current distortions and head motions using FSL8, the dMRI images were analyzed under the FM-based framework and the FM-related parameters, the Noah exponent α and the Hurst exponent H, were calculated2. In addition, ADC maps were also obtained using the images acquired at b-values of 0 and 972 s/mm2. In analogy with the diffusion tensor, α and H along the gradient direction $$$\hat{n}=({{n}_{x}},{{n}_{y}},{{n}_{z}})^{T}$$$ are related to the symmetric and positive definite tensors (A and H) by the following equations: $$\alpha (\hat{n})={{\mathbf{\hat{n}}}^{T}}\cdot \mathbf{A}\cdot \mathbf{\hat{n}}$$and $$H(\mathbf{\hat{n}})={{\mathbf{\hat{n}}}^{T}}\cdot \mathbf{H}\cdot \mathbf{\hat{n}}$$Following the diffusion tensor model, the obtained tensors were then diagonalized to obtain the eigenvalues (λ1, λ2 and λ3 in descending order) and the corresponding eigenvectors (v1, v2 and v3). Fractional anisotropy (FA) and linear cl, planar cp, and spherical cs, tensor shape measures were then calculated9.
Results
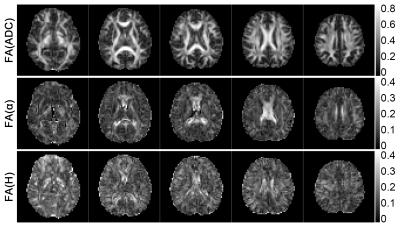
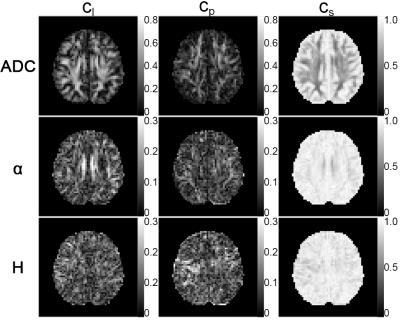
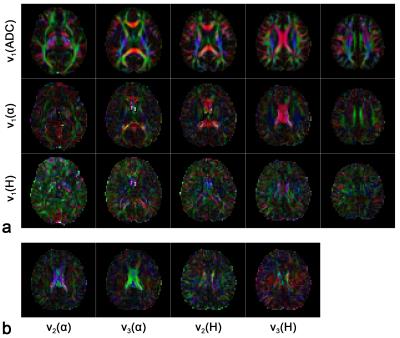
The FA maps for ADC, α and H are shown in Figure 2. The anisotropy of the FM-related parameters could be seen, although to a less extent comparing to ADC. On the other hand, difference between α and H in terms of directional sensitivity was observed. FA maps of α showed similar contrast pattern as ADC. In particular, FA values in corpus callosum and cingulum were obviously higher, which correspond to the fiber structure. In contrast, FA values for H were not as high as α in these regions. Similar results can be observed in the shape measure maps shown in Figure 3 since α showed stronger linearity in cingulum than H. Therefore, α is more sensitive to the anatomical structures as compared to H. The orientations of the eigenvectors are shown in the color encoded map in Figure 4. The principle eigenvector of α (v1(α)) featured similar orientations to the principle eigenvector of ADC (v1(ADC)), implying that α is also heavily influenced by the fiber tract. On the other hand, no correlation between the eigenvectors of H and fiber orientation was seen.Discussion and Conclusion
In this study, the FM-related parameters were obtained in 12 directions and the directional sensitivity was assessed. Both α and H were seen to be sensitive to the directions of applied diffusion gradients albeit with lower level of directional sensitivity as compared to ADC. On the other hand, α was found to reflect the fiber structure in white matter as ADC while H exhibited quite different directional information. Although it is not clear if tensor model best suits the directionality of FM-related parameters, it is a convenient approach for the first attempt. To fully clarify this issue, an accurate anisotropic model is needed. In summary, exploring the directional sensitivity in FM model may provide new insight of the brain microstructure.Acknowledgements
No acknowledgement found.References
1. De Santis S, Gabrielli A, Palombo M, et al. Non-Gaussian diffusion imaging: a brief practical review. Magn Reson Imaging 2011;29:1410–6.
2. Fan Y, Gao J-H. Fractional motion model for characterization of anomalous diffusion from NMR signals. Phys Rev E 2015;92:12707.
3. Magdziarz M, Weron A, Burnecki K, et al. Fractional brownian motion versus the continuous-time random walk: a simple test for subdiffusive dynamics. Phys Rev Lett 2009;103:180602.
4. Szymanski J, Weiss M. Elucidating the origin of anomalous diffusion in crowded fluids. Phys Rev Lett 2009;103:38102.
5. Chenevert TL, Brunberg JA, Pipe JG. Anisotropic diffusion in human white matter: demonstration with MR techniques in vivo. Radiology 1990;177:401–5.
6. Moseley ME, Cohen Y, Kucharczyk J, et al. Diffusion-weighted MR imaging of anisotropic water diffusion in cat central nervous system. Radiology 1990;176:439–45.
7. Basser PJ, Özarslan E. Anisotropic diffusion: from the apparent diffusion coefficient to the apparent diffusion tensor. In: Jones, PhD DK, ed. Diffusion MRI. Oxford University Press; 2010:79–91.
8. Smith SM, Jenkinson M, Woolrich MW, et al. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage 2004;23, Supplement 1:S208–19.
9. Westin C-F, Maier SE, Mamata H, et al.
Processing and visualization for diffusion tensor MRI. Med Image Anal
2002;6:93–108.
Figures